$μ$PC: Scaling Predictive Coding to 100+ Layer Networks

The biological implausibility of backpropagation (BP) has motivated many alternative, brain-inspired algorithms that attempt to rely only on local information, such as predictive coding (PC) and equilibrium propagation. However, these algorithms have notoriously struggled to train very deep networks, preventing them from competing with BP in large-scale settings. Indeed, scaling PC networks (PCNs) has recently been posed as a challenge for the community (Pinchetti et al., 2024). Here, we show that 100+ layer PCNs can be trained reliably using a Depth-$\mu$P parameterisation (Yang et al., 2023; Bordelon et al., 2023) which we call "$\mu$PC". Through an extensive analysis of the scaling behaviour of PCNs, we reveal several pathologies that make standard PCNs difficult to train at large depths. We then show that, despite addressing only some of these instabilities, $\mu$PC allows stable training of very deep (up to 128-layer) residual networks on simple classification tasks with competitive performance and little tuning compared to current benchmarks. Moreover, $\mu$PC enables zero-shot transfer of both weight and activity learning rates across widths and depths. Our results have implications for other local algorithms and could be extended to convolutional and transformer architectures. Code for $\mu$PC is made available as part of a JAX library for PCNs at https://github.com/thebuckleylab/jpc (Innocenti et al., 2024).

Only Strict Saddles in the Energy Landscape of Predictive Coding Networks?

Predictive coding (PC) is an energy-based learning algorithm that performs iterative inference over network activities before weight updates. Recent work suggests that PC can converge in fewer learning steps than backpropagation thanks to its inference procedure. However, these advantages are not always observed, and the impact of PC inference on learning is theoretically not well understood. Here, we study the geometry of the PC energy landscape at the (inference) equilibrium of the network activities. For deep linear networks, we first show that the equilibrated energy is simply a rescaled mean squared error loss with a weight-dependent rescaling. We then prove that many highly degenerate (non-strict) saddles of the loss including the origin become much easier to escape (strict) in the equilibrated energy. Our theory is validated by experiments on both linear and non-linear networks. Based on these results, we conjecture that all the saddles of the equilibrated energy are strict. Overall, this work suggests that PC inference makes the loss landscape more benign and robust to vanishing gradients, while also highlighting the challenge of speeding up PC inference on large-scale models.

A general approximation lower bound in $L^p$ norm, with applications to feed-forward neural networks

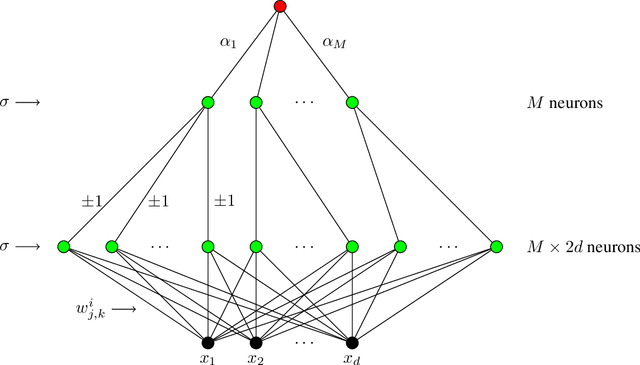
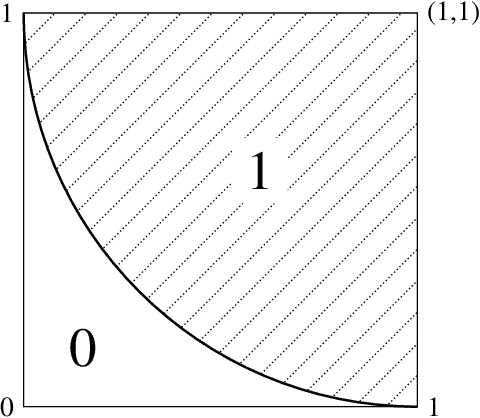
We study the fundamental limits to the expressive power of neural networks. Given two sets $F$, $G$ of real-valued functions, we first prove a general lower bound on how well functions in $F$ can be approximated in $L^p(\mu)$ norm by functions in $G$, for any $p \geq 1$ and any probability measure $\mu$. The lower bound depends on the packing number of $F$, the range of $F$, and the fat-shattering dimension of $G$. We then instantiate this bound to the case where $G$ corresponds to a piecewise-polynomial feed-forward neural network, and describe in details the application to two sets $F$: H{\"o}lder balls and multivariate monotonic functions. Beside matching (known or new) upper bounds up to log factors, our lower bounds shed some light on the similarities or differences between approximation in $L^p$ norm or in sup norm, solving an open question by DeVore et al. (2021). Our proof strategy differs from the sup norm case and uses a key probability result of Mendelson (2002).