Predictive Pipelined Decoding: A Compute-Latency Trade-off for Exact LLM Decoding

This paper presents "Predictive Pipelined Decoding (PPD)," an approach that speeds up greedy decoding in Large Language Models (LLMs) while maintaining the exact same output as the original decoding. Unlike conventional strategies, PPD employs additional compute resources to parallelize the initiation of subsequent token decoding during the current token decoding. This innovative method reduces decoding latency and reshapes the understanding of trade-offs in LLM decoding strategies. We have developed a theoretical framework that allows us to analyze the trade-off between computation and latency. Using this framework, we can analytically estimate the potential reduction in latency associated with our proposed method, achieved through the assessment of the match rate, represented as p_correct. The results demonstrate that the use of extra computational resources has the potential to accelerate LLM greedy decoding.

Teaching Arithmetic to Small Transformers

Large language models like GPT-4 exhibit emergent capabilities across general-purpose tasks, such as basic arithmetic, when trained on extensive text data, even though these tasks are not explicitly encoded by the unsupervised, next-token prediction objective. This study investigates how small transformers, trained from random initialization, can efficiently learn arithmetic operations such as addition, multiplication, and elementary functions like square root, using the next-token prediction objective. We first demonstrate that conventional training data is not the most effective for arithmetic learning, and simple formatting changes can significantly improve accuracy. This leads to sharp phase transitions as a function of training data scale, which, in some cases, can be explained through connections to low-rank matrix completion. Building on prior work, we then train on chain-of-thought style data that includes intermediate step results. Even in the complete absence of pretraining, this approach significantly and simultaneously improves accuracy, sample complexity, and convergence speed. We also study the interplay between arithmetic and text data during training and examine the effects of few-shot prompting, pretraining, and model scale. Additionally, we discuss length generalization challenges. Our work highlights the importance of high-quality, instructive data that considers the particular characteristics of the next-word prediction objective for rapidly eliciting arithmetic capabilities.

DPOK: Reinforcement Learning for Fine-tuning Text-to-Image Diffusion Models

Learning from human feedback has been shown to improve text-to-image models. These techniques first learn a reward function that captures what humans care about in the task and then improve the models based on the learned reward function. Even though relatively simple approaches (e.g., rejection sampling based on reward scores) have been investigated, fine-tuning text-to-image models with the reward function remains challenging. In this work, we propose using online reinforcement learning (RL) to fine-tune text-to-image models. We focus on diffusion models, defining the fine-tuning task as an RL problem, and updating the pre-trained text-to-image diffusion models using policy gradient to maximize the feedback-trained reward. Our approach, coined DPOK, integrates policy optimization with KL regularization. We conduct an analysis of KL regularization for both RL fine-tuning and supervised fine-tuning. In our experiments, we show that DPOK is generally superior to supervised fine-tuning with respect to both image-text alignment and image quality.

Vector-Valued Variation Spaces and Width Bounds for DNNs: Insights on Weight Decay Regularization

Deep neural networks (DNNs) trained to minimize a loss term plus the sum of squared weights via gradient descent corresponds to the common approach of training with weight decay. This paper provides new insights into this common learning framework. We characterize the kinds of functions learned by training with weight decay for multi-output (vector-valued) ReLU neural networks. This extends previous characterizations that were limited to single-output (scalar-valued) networks. This characterization requires the definition of a new class of neural function spaces that we call vector-valued variation (VV) spaces. We prove that neural networks (NNs) are optimal solutions to learning problems posed over VV spaces via a novel representer theorem. This new representer theorem shows that solutions to these learning problems exist as vector-valued neural networks with widths bounded in terms of the number of training data. Next, via a novel connection to the multi-task lasso problem, we derive new and tighter bounds on the widths of homogeneous layers in DNNs. The bounds are determined by the effective dimensions of the training data embeddings in/out of the layers. This result sheds new light on the architectural requirements for DNNs. Finally, the connection to the multi-task lasso problem suggests a new approach to compressing pre-trained networks.

Prompted LLMs as Chatbot Modules for Long Open-domain Conversation

In this paper, we propose MPC (Modular Prompted Chatbot), a new approach for creating high-quality conversational agents without the need for fine-tuning. Our method utilizes pre-trained large language models (LLMs) as individual modules for long-term consistency and flexibility, by using techniques such as few-shot prompting, chain-of-thought (CoT), and external memory. Our human evaluation results show that MPC is on par with fine-tuned chatbot models in open-domain conversations, making it an effective solution for creating consistent and engaging chatbots.

Improving Fair Training under Correlation Shifts

Model fairness is an essential element for Trustworthy AI. While many techniques for model fairness have been proposed, most of them assume that the training and deployment data distributions are identical, which is often not true in practice. In particular, when the bias between labels and sensitive groups changes, the fairness of the trained model is directly influenced and can worsen. We make two contributions for solving this problem. First, we analytically show that existing in-processing fair algorithms have fundamental limits in accuracy and group fairness. We introduce the notion of correlation shifts, which can explicitly capture the change of the above bias. Second, we propose a novel pre-processing step that samples the input data to reduce correlation shifts and thus enables the in-processing approaches to overcome their limitations. We formulate an optimization problem for adjusting the data ratio among labels and sensitive groups to reflect the shifted correlation. A key benefit of our approach lies in decoupling the roles of pre- and in-processing approaches: correlation adjustment via pre-processing and unfairness mitigation on the processed data via in-processing. Experiments show that our framework effectively improves existing in-processing fair algorithms w.r.t. accuracy and fairness, both on synthetic and real datasets.

Optimizing DDPM Sampling with Shortcut Fine-Tuning

In this study, we propose Shortcut Fine-Tuning (SFT), a new approach for addressing the challenge of fast sampling of pretrained Denoising Diffusion Probabilistic Models (DDPMs). SFT advocates for the fine-tuning of DDPM samplers through the direct minimization of Integral Probability Metrics (IPM), instead of learning the backward diffusion process. This enables samplers to discover an alternative and more efficient sampling shortcut, deviating from the backward diffusion process. We also propose a new algorithm that is similar to the policy gradient method for fine-tuning DDPMs by proving that under certain assumptions, the gradient descent of diffusion models is equivalent to the policy gradient approach. Through empirical evaluation, we demonstrate that our fine-tuning method can further enhance existing fast DDPM samplers, resulting in sample quality comparable to or even surpassing that of the full-step model across various datasets.

Looped Transformers as Programmable Computers

We present a framework for using transformer networks as universal computers by programming them with specific weights and placing them in a loop. Our input sequence acts as a punchcard, consisting of instructions and memory for data read/writes. We demonstrate that a constant number of encoder layers can emulate basic computing blocks, including embedding edit operations, non-linear functions, function calls, program counters, and conditional branches. Using these building blocks, we emulate a small instruction-set computer. This allows us to map iterative algorithms to programs that can be executed by a looped, 13-layer transformer. We show how this transformer, instructed by its input, can emulate a basic calculator, a basic linear algebra library, and in-context learning algorithms that employ backpropagation. Our work highlights the versatility of the attention mechanism, and demonstrates that even shallow transformers can execute full-fledged, general-purpose programs.

Score-based Generative Modeling Secretly Minimizes the Wasserstein Distance

Score-based generative models are shown to achieve remarkable empirical performances in various applications such as image generation and audio synthesis. However, a theoretical understanding of score-based diffusion models is still incomplete. Recently, Song et al. showed that the training objective of score-based generative models is equivalent to minimizing the Kullback-Leibler divergence of the generated distribution from the data distribution. In this work, we show that score-based models also minimize the Wasserstein distance between them under suitable assumptions on the model. Specifically, we prove that the Wasserstein distance is upper bounded by the square root of the objective function up to multiplicative constants and a fixed constant offset. Our proof is based on a novel application of the theory of optimal transport, which can be of independent interest to the society. Our numerical experiments support our findings. By analyzing our upper bounds, we provide a few techniques to obtain tighter upper bounds.

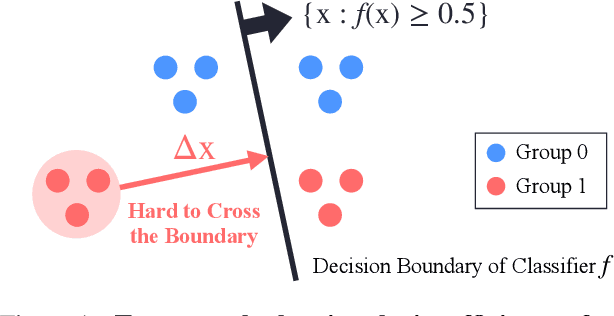
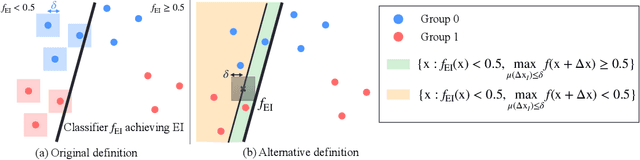
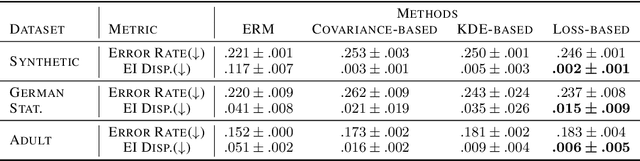
Equal Improvability: A New Fairness Notion Considering the Long-term Impact

Devising a fair classifier that does not discriminate against different groups is an important problem in machine learning. Although researchers have proposed various ways of defining group fairness, most of them only focused on the immediate fairness, ignoring the long-term impact of a fair classifier under the dynamic scenario where each individual can improve its feature over time. Such dynamic scenarios happen in real world, e.g., college admission and credit loaning, where each rejected sample makes effort to change its features to get accepted afterwards. In this dynamic setting, the long-term fairness should equalize the samples' feature distribution across different groups after the rejected samples make some effort to improve. In order to promote long-term fairness, we propose a new fairness notion called Equal Improvability (EI), which equalizes the potential acceptance rate of the rejected samples across different groups assuming a bounded level of effort will be spent by each rejected sample. We analyze the properties of EI and its connections with existing fairness notions. To find a classifier that satisfies the EI requirement, we propose and study three different approaches that solve EI-regularized optimization problems. Through experiments on both synthetic and real datasets, we demonstrate that the proposed EI-regularized algorithms encourage us to find a fair classifier in terms of EI. Finally, we provide experimental results on dynamic scenarios which highlight the advantages of our EI metric in achieving the long-term fairness. Codes are available in a GitHub repository, see https://github.com/guldoganozgur/ei_fairness.