Maestro: Uncovering Low-Rank Structures via Trainable Decomposition

Deep Neural Networks (DNNs) have been a large driver and enabler for AI breakthroughs in recent years. These models have been getting larger in their attempt to become more accurate and tackle new upcoming use-cases, including AR/VR and intelligent assistants. However, the training process of such large models is a costly and time-consuming process, which typically yields a single model to fit all targets. To mitigate this, various techniques have been proposed in the literature, including pruning, sparsification or quantization of the model weights and updates. While able to achieve high compression rates, they often incur computational overheads or accuracy penalties. Alternatively, factorization methods have been leveraged to incorporate low-rank compression in the training process. Similarly, such techniques (e.g.,~SVD) frequently rely on the computationally expensive decomposition of layers and are potentially sub-optimal for non-linear models, such as DNNs. In this work, we take a further step in designing efficient low-rank models and propose Maestro, a framework for trainable low-rank layers. Instead of regularly applying a priori decompositions such as SVD, the low-rank structure is built into the training process through a generalized variant of Ordered Dropout. This method imposes an importance ordering via sampling on the decomposed DNN structure. Our theoretical analysis demonstrates that our method recovers the SVD decomposition of linear mapping on uniformly distributed data and PCA for linear autoencoders. We further apply our technique on DNNs and empirically illustrate that Maestro enables the extraction of lower footprint models that preserve model performance while allowing for graceful accuracy-latency tradeoff for the deployment to devices of different capabilities.

Recommender Systems with Generative Retrieval

Modern recommender systems leverage large-scale retrieval models consisting of two stages: training a dual-encoder model to embed queries and candidates in the same space, followed by an Approximate Nearest Neighbor (ANN) search to select top candidates given a query's embedding. In this paper, we propose a new single-stage paradigm: a generative retrieval model which autoregressively decodes the identifiers for the target candidates in one phase. To do this, instead of assigning randomly generated atomic IDs to each item, we generate Semantic IDs: a semantically meaningful tuple of codewords for each item that serves as its unique identifier. We use a hierarchical method called RQ-VAE to generate these codewords. Once we have the Semantic IDs for all the items, a Transformer based sequence-to-sequence model is trained to predict the Semantic ID of the next item. Since this model predicts the tuple of codewords identifying the next item directly in an autoregressive manner, it can be considered a generative retrieval model. We show that our recommender system trained in this new paradigm improves the results achieved by current SOTA models on the Amazon dataset. Moreover, we demonstrate that the sequence-to-sequence model coupled with hierarchical Semantic IDs offers better generalization and hence improves retrieval of cold-start items for recommendations.

The Expressive Power of Tuning Only the Norm Layers

Feature normalization transforms such as Batch and Layer-Normalization have become indispensable ingredients of state-of-the-art deep neural networks. Recent studies on fine-tuning large pretrained models indicate that just tuning the parameters of these affine transforms can achieve high accuracy for downstream tasks. These findings open the questions about the expressive power of tuning the normalization layers of frozen networks. In this work, we take the first step towards this question and show that for random ReLU networks, fine-tuning only its normalization layers can reconstruct any target network that is $O(\sqrt{\text{width}})$ times smaller. We show that this holds even for randomly sparsified networks, under sufficient overparameterization, in agreement with prior empirical work.

Looped Transformers as Programmable Computers

We present a framework for using transformer networks as universal computers by programming them with specific weights and placing them in a loop. Our input sequence acts as a punchcard, consisting of instructions and memory for data read/writes. We demonstrate that a constant number of encoder layers can emulate basic computing blocks, including embedding edit operations, non-linear functions, function calls, program counters, and conditional branches. Using these building blocks, we emulate a small instruction-set computer. This allows us to map iterative algorithms to programs that can be executed by a looped, 13-layer transformer. We show how this transformer, instructed by its input, can emulate a basic calculator, a basic linear algebra library, and in-context learning algorithms that employ backpropagation. Our work highlights the versatility of the attention mechanism, and demonstrates that even shallow transformers can execute full-fledged, general-purpose programs.

LIFT: Language-Interfaced Fine-Tuning for Non-Language Machine Learning Tasks

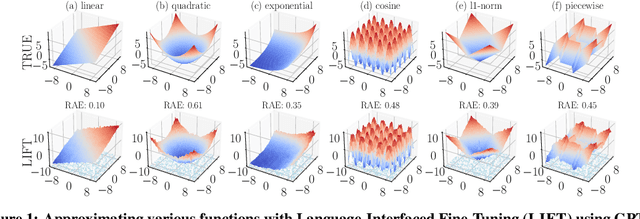
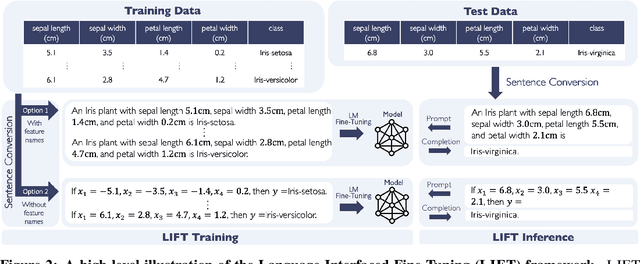
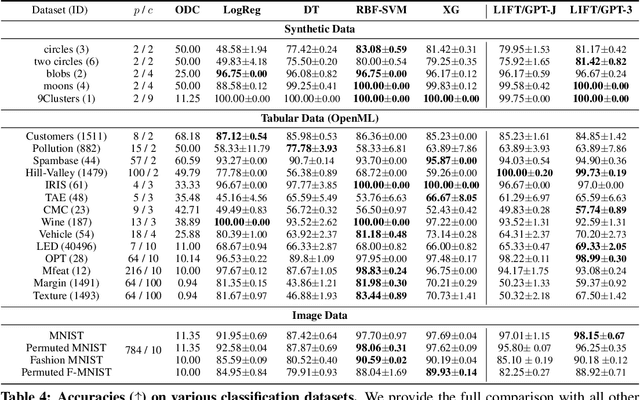
Fine-tuning pretrained language models (LMs) without making any architectural changes has become a norm for learning various language downstream tasks. However, for non-language downstream tasks, a common practice is to employ task-specific designs for input, output layers, and loss functions. For instance, it is possible to fine-tune an LM into an MNIST classifier by replacing the word embedding layer with an image patch embedding layer, the word token output layer with a 10-way output layer, and the word prediction loss with a 10-way classification loss, respectively. A natural question arises: can LM fine-tuning solve non-language downstream tasks without changing the model architecture or loss function? To answer this, we propose Language-Interfaced Fine-Tuning (LIFT) and study its efficacy and limitations by conducting an extensive empirical study on a suite of non-language classification and regression tasks. LIFT does not make any changes to the model architecture or loss function, and it solely relies on the natural language interface, enabling "no-code machine learning with LMs." We find that LIFT performs relatively well across a wide range of low-dimensional classification and regression tasks, matching the performances of the best baselines in many cases, especially for the classification tasks. We report the experimental results on the fundamental properties of LIFT, including its inductive bias, sample efficiency, ability to extrapolate, robustness to outliers and label noise, and generalization. We also analyze a few properties/techniques specific to LIFT, e.g., context-aware learning via appropriate prompting, quantification of predictive uncertainty, and two-stage fine-tuning. Our code is available at https://github.com/UW-Madison-Lee-Lab/LanguageInterfacedFineTuning.

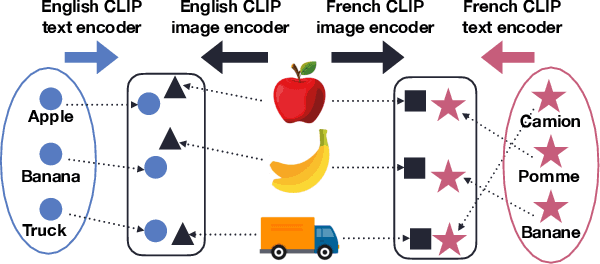
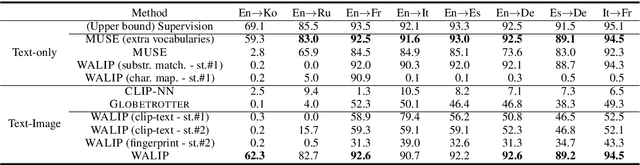
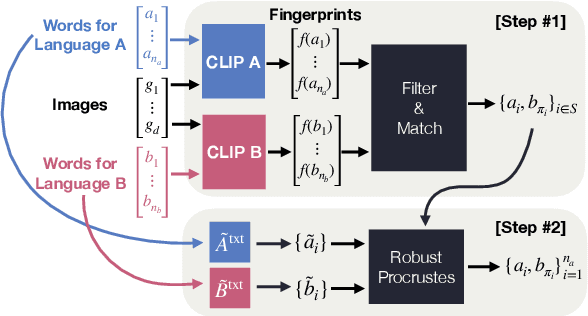
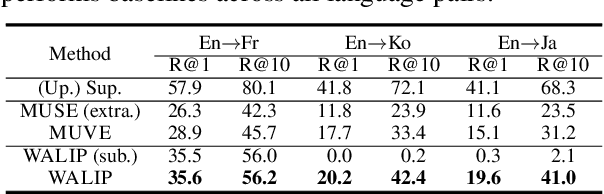
Utilizing Language-Image Pretraining for Efficient and Robust Bilingual Word Alignment

Word translation without parallel corpora has become feasible, rivaling the performance of supervised methods. Recent findings have shown that the accuracy and robustness of unsupervised word translation (UWT) can be improved by making use of visual observations, which are universal representations across languages. In this work, we investigate the potential of using not only visual observations but also pretrained language-image models for enabling a more efficient and robust UWT. Specifically, we develop a novel UWT method dubbed Word Alignment using Language-Image Pretraining (WALIP), which leverages visual observations via the shared embedding space of images and texts provided by CLIP models (Radford et al., 2021). WALIP has a two-step procedure. First, we retrieve word pairs with high confidences of similarity, computed using our proposed image-based fingerprints, which define the initial pivot for the word alignment. Second, we apply our robust Procrustes algorithm to estimate the linear mapping between two embedding spaces, which iteratively corrects and refines the estimated alignment. Our extensive experiments show that WALIP improves upon the state-of-the-art performance of bilingual word alignment for a few language pairs across different word embeddings and displays great robustness to the dissimilarity of language pairs or training corpora for two word embeddings.

Finding Everything within Random Binary Networks

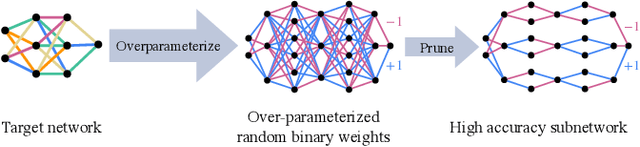
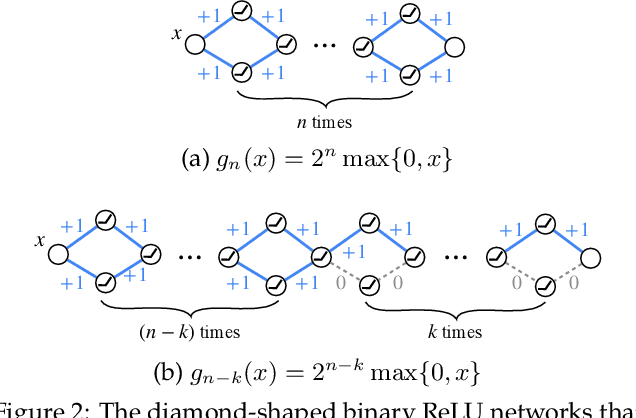
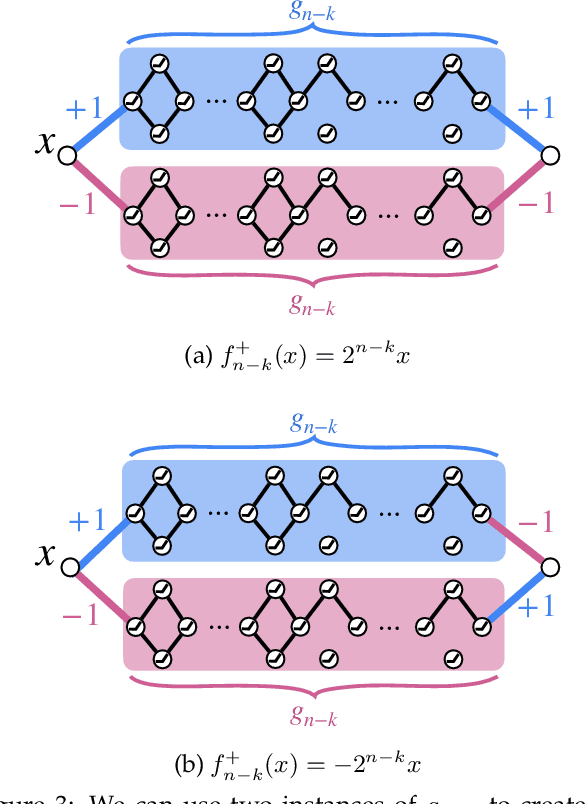
A recent work by Ramanujan et al. (2020) provides significant empirical evidence that sufficiently overparameterized, random neural networks contain untrained subnetworks that achieve state-of-the-art accuracy on several predictive tasks. A follow-up line of theoretical work provides justification of these findings by proving that slightly overparameterized neural networks, with commonly used continuous-valued random initializations can indeed be pruned to approximate any target network. In this work, we show that the amplitude of those random weights does not even matter. We prove that any target network can be approximated up to arbitrary accuracy by simply pruning a random network of binary $\{\pm1\}$ weights that is only a polylogarithmic factor wider and deeper than the target network.

Minibatch vs Local SGD with Shuffling: Tight Convergence Bounds and Beyond

In distributed learning, local SGD (also known as federated averaging) and its simple baseline minibatch SGD are widely studied optimization methods. Most existing analyses of these methods assume independent and unbiased gradient estimates obtained via with-replacement sampling. In contrast, we study shuffling-based variants: minibatch and local Random Reshuffling, which draw stochastic gradients without replacement and are thus closer to practice. For smooth functions satisfying the Polyak-{\L}ojasiewicz condition, we obtain convergence bounds (in the large epoch regime) which show that these shuffling-based variants converge faster than their with-replacement counterparts. Moreover, we prove matching lower bounds showing that our convergence analysis is tight. Finally, we propose an algorithmic modification called synchronized shuffling that leads to convergence rates faster than our lower bounds in near-homogeneous settings.

An Exponential Improvement on the Memorization Capacity of Deep Threshold Networks

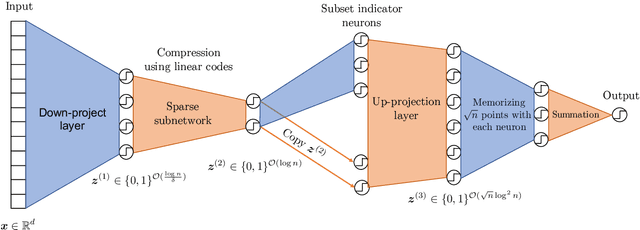
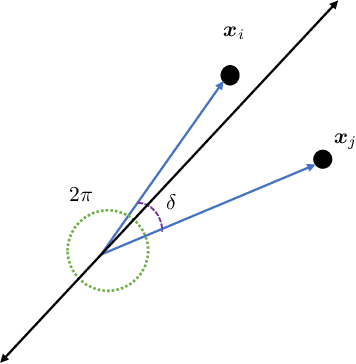
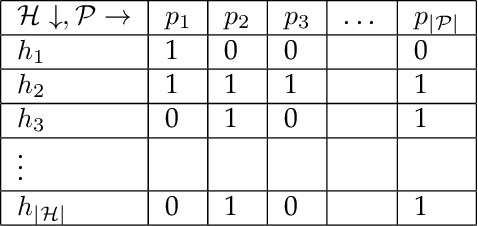
It is well known that modern deep neural networks are powerful enough to memorize datasets even when the labels have been randomized. Recently, Vershynin (2020) settled a long standing question by Baum (1988), proving that \emph{deep threshold} networks can memorize $n$ points in $d$ dimensions using $\widetilde{\mathcal{O}}(e^{1/\delta^2}+\sqrt{n})$ neurons and $\widetilde{\mathcal{O}}(e^{1/\delta^2}(d+\sqrt{n})+n)$ weights, where $\delta$ is the minimum distance between the points. In this work, we improve the dependence on $\delta$ from exponential to almost linear, proving that $\widetilde{\mathcal{O}}(\frac{1}{\delta}+\sqrt{n})$ neurons and $\widetilde{\mathcal{O}}(\frac{d}{\delta}+n)$ weights are sufficient. Our construction uses Gaussian random weights only in the first layer, while all the subsequent layers use binary or integer weights. We also prove new lower bounds by connecting memorization in neural networks to the purely geometric problem of separating $n$ points on a sphere using hyperplanes.

Permutation-Based SGD: Is Random Optimal?

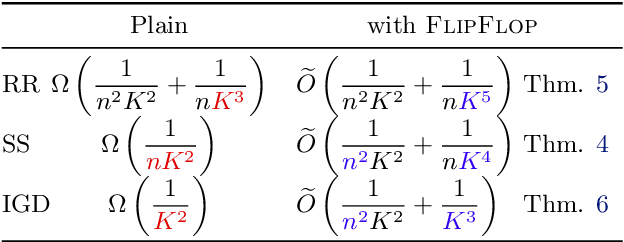
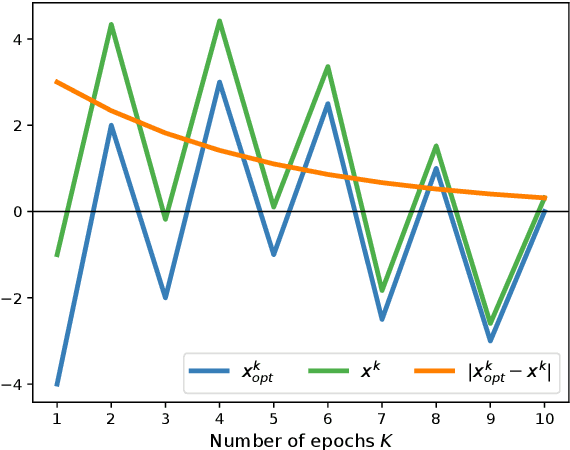
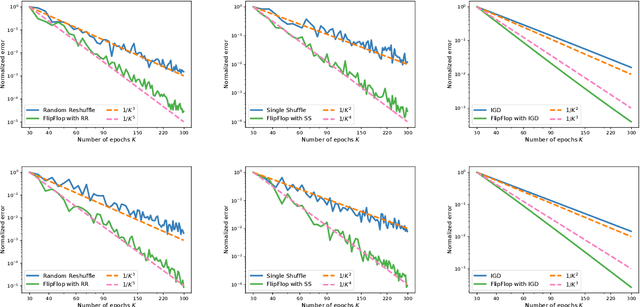
A recent line of ground-breaking results for permutation-based SGD has corroborated a widely observed phenomenon: random permutations offer faster convergence than with-replacement sampling. However, is random optimal? We show that this depends heavily on what functions we are optimizing, and the convergence gap between optimal and random permutations can vary from exponential to nonexistent. We first show that for 1-dimensional strongly convex functions, with smooth second derivatives, there exist optimal permutations that offer exponentially faster convergence compared to random. However, for general strongly convex functions, random permutations are optimal. Finally, we show that for quadratic, strongly-convex functions, there are easy-to-construct permutations that lead to accelerated convergence compared to random. Our results suggest that a general convergence characterization of optimal permutations cannot capture the nuances of individual function classes, and can mistakenly indicate that one cannot do much better than random.