Real-time Human Activity Recognition Using Conditionally Parametrized Convolutions on Mobile and Wearable Devices

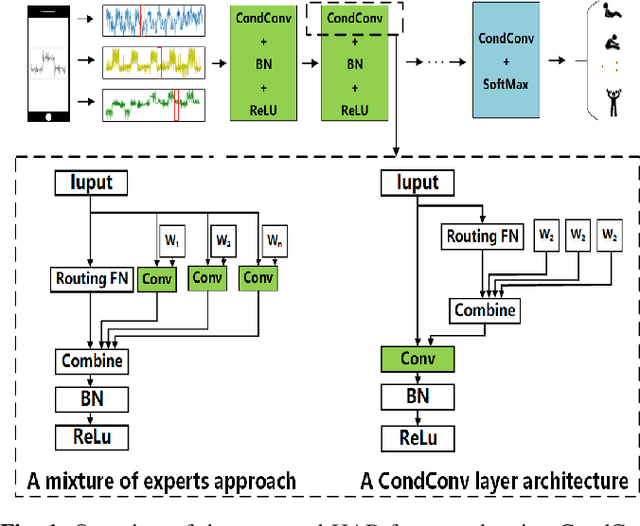
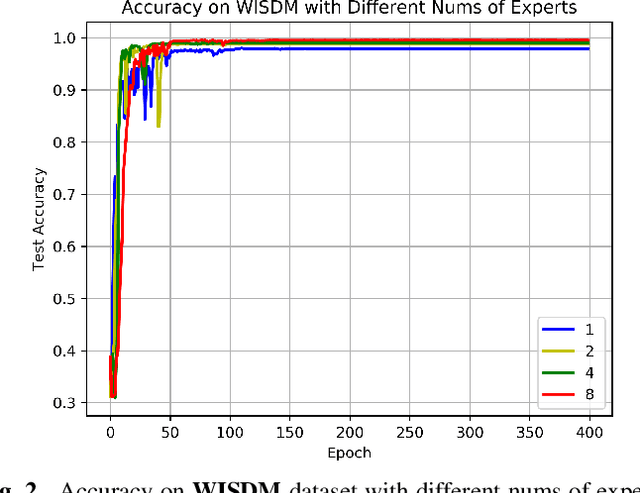
Recently, deep learning has represented an important research trend in human activity recognition (HAR). In particular, deep convolutional neural networks (CNNs) have achieved state-of-the-art performance on various HAR datasets. For deep learning, improvements in performance have to heavily rely on increasing model size or capacity to scale to larger and larger datasets, which inevitably leads to the increase of operations. A high number of operations in deep leaning increases computational cost and is not suitable for real-time HAR using mobile and wearable sensors. Though shallow learning techniques often are lightweight, they could not achieve good performance. Therefore, deep learning methods that can balance the trade-off between accuracy and computation cost is highly needed, which to our knowledge has seldom been researched. In this paper, we for the first time propose a computation efficient CNN using conditionally parametrized convolution for real-time HAR on mobile and wearable devices. We evaluate the proposed method on four public benchmark HAR datasets consisting of WISDM dataset, PAMAP2 dataset, UNIMIB-SHAR dataset, and OPPORTUNITY dataset, achieving state-of-the-art accuracy without compromising computation cost. Various ablation experiments are performed to show how such a network with large capacity is clearly preferable to baseline while requiring a similar amount of operations. The method can be used as a drop-in replacement for the existing deep HAR architectures and easily deployed onto mobile and wearable devices for real-time HAR applications.

Memory-Augmented Relation Network for Few-Shot Learning

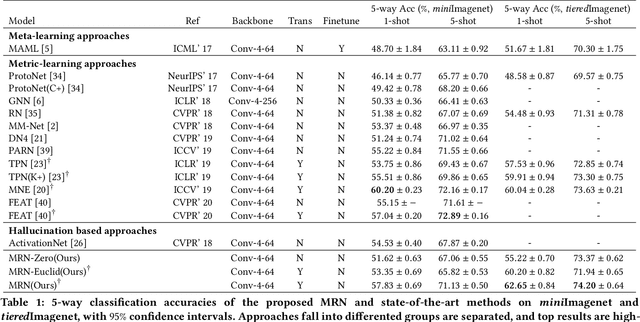
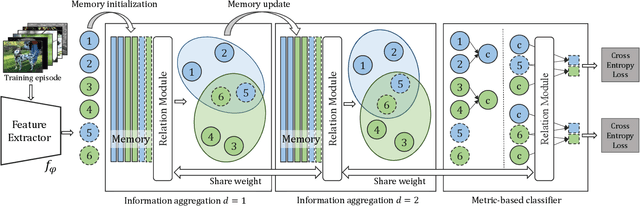
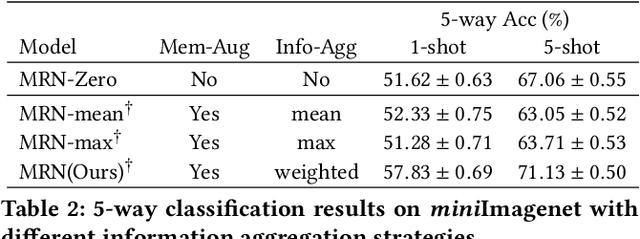
Metric-based few-shot learning methods concentrate on learning transferable feature embedding that generalizes well from seen categories to unseen categories under the supervision of limited number of labelled instances. However, most of them treat each individual instance in the working context separately without considering its relationships with the others. In this work, we investigate a new metric-learning method, Memory-Augmented Relation Network (MRN), to explicitly exploit these relationships. In particular, for an instance, we choose the samples that are visually similar from the working context, and perform weighted information propagation to attentively aggregate helpful information from the chosen ones to enhance its representation. In MRN, we also formulate the distance metric as a learnable relation module which learns to compare for similarity measurement, and augment the working context with memory slots, both contributing to its generality. We empirically demonstrate that MRN yields significant improvement over its ancestor and achieves competitive or even better performance when compared with other few-shot learning approaches on the two major benchmark datasets, i.e. miniImagenet and tieredImagenet.

Efficient convolutional neural networks with smaller filters for human activity recognition using wearable sensors

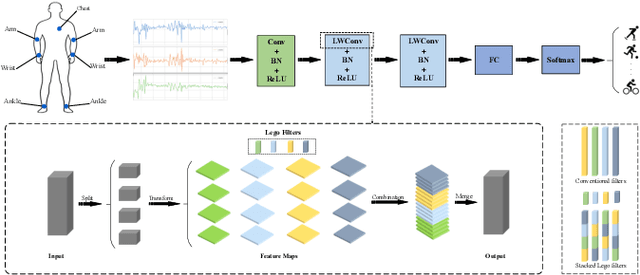
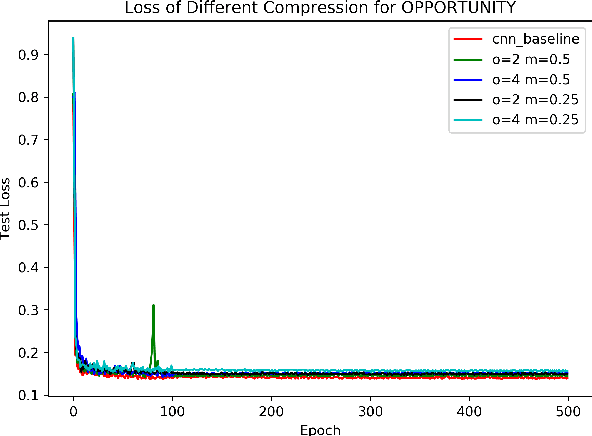
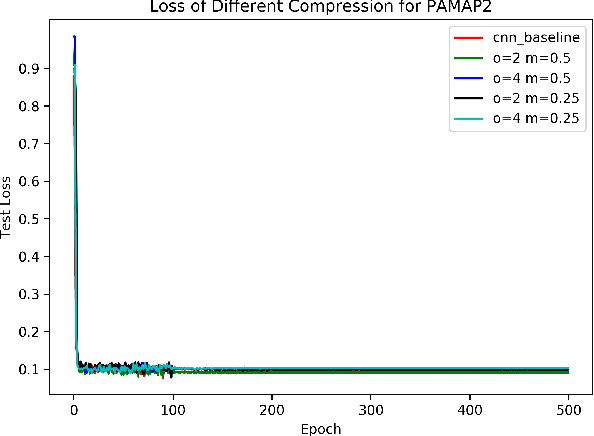
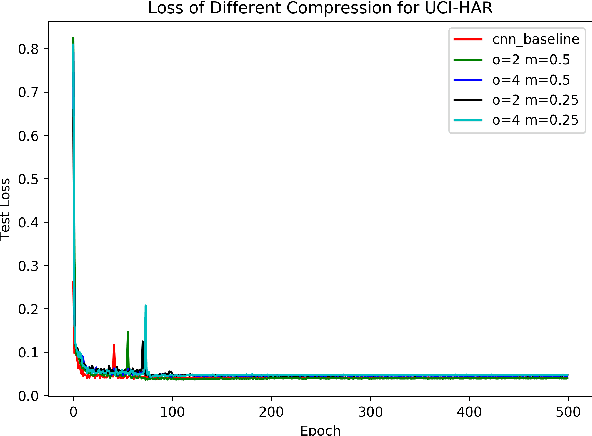
Recently, human activity recognition (HAR) has been beginning to adopt deep learning to substitute for traditional shallow learning techniques that rely on hand-crafted features. CNNs, in particular, have set latest state-of-the-art on various HAR datasets. However, deep model often requires more computing resources, which limits its applications in embedded HAR. Although many successful methods have been proposed to reduce memory and FLOPs of CNNs, they often involve special network architectures for visual tasks, which are not suitable for deep HAR tasks with time series sensor signals, due to remarkable discrepancy. Therefore, it is necessary to develop lightweight deep models to perform HAR. As filter is the basic unit in constructing CNNs, we must ask whether redesigning smaller filters is applicable for deep HAR. In the paper, inspired by the idea, we proposed a lightweight CNN using re-designed Lego filters for the use of HAR. A set of lower-dimensional filters is used as Lego bricks to be stacked for conventional filters, which does not rely on any special network structure. To our knowledge, this is the first paper that proposes lightweight CNN for HAR in ubiquitous and wearable computing arena. The experiment results on five public HAR datasets, UCI-HAR dataset, OPPORTUNITY dataset, UNIMIB-SHAR dataset, PAMAP2 dataset, and WISDM dataset, indicate that our novel Lego-CNN approach can greatly reduce memory and computation cost over CNN, while maintaining comparable accuracy. We believe that the proposed approach could combine with the existing state-of-the-art HAR architecture and easily deployed onto wearable devices for real HAR applications.

Incorporating Multiple Cluster Centers for Multi-Label Learning

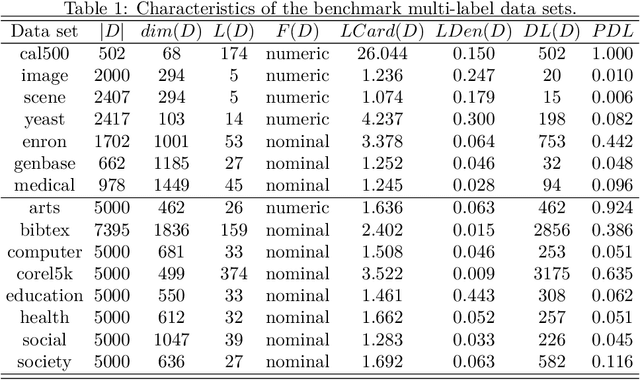
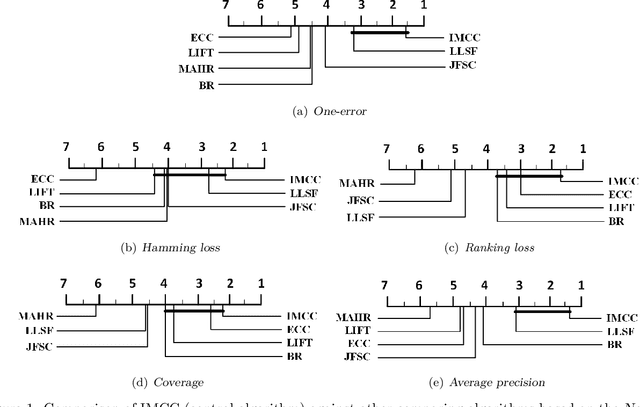
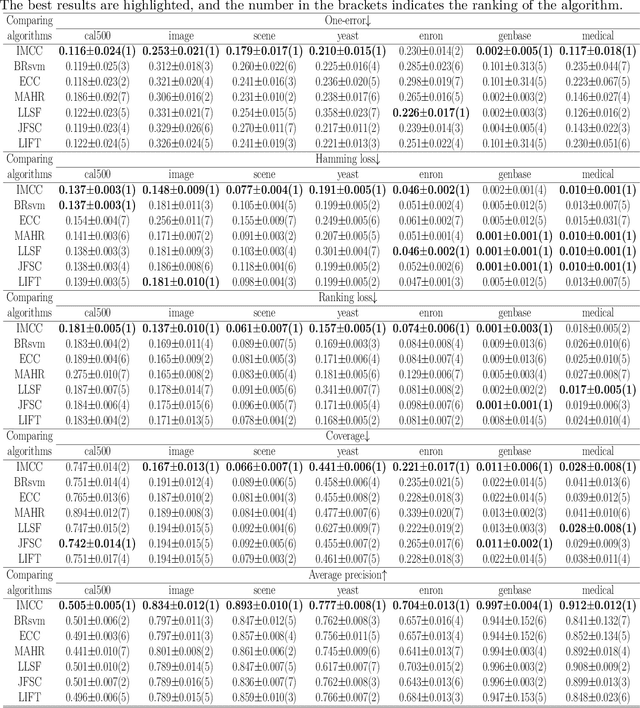
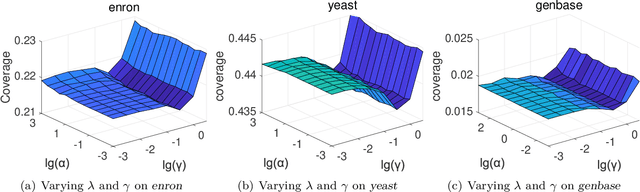
Multi-label learning deals with the problem that each instance is associated with multiple labels simultaneously. Most of the existing approaches aim to improve the performance of multi-label learning by exploiting label correlations. Although the data augmentation technique is widely used in many machine learning tasks, it is still unclear whether data augmentation is helpful to multi-label learning. In this paper, (to the best of our knowledge) we provide the first attempt to leverage the data augmentation technique to improve the performance of multi-label learning. Specifically, we first propose a novel data augmentation approach that performs clustering on the real examples and treats the cluster centers as virtual examples, and these virtual examples naturally embody the local label correlations and label importances. Then, motivated by the cluster assumption that examples in the same cluster should have the same label, we propose a novel regularization term to bridge the gap between the real examples and virtual examples, which can promote the local smoothness of the learning function. Extensive experimental results on a number of real-world multi-label data sets clearly demonstrate that our proposed approach outperforms the state-of-the-art counterparts.

Sequential Weakly Labeled Multi-Activity Recognition and Location on Wearable Sensors using Recurrent Attention Network

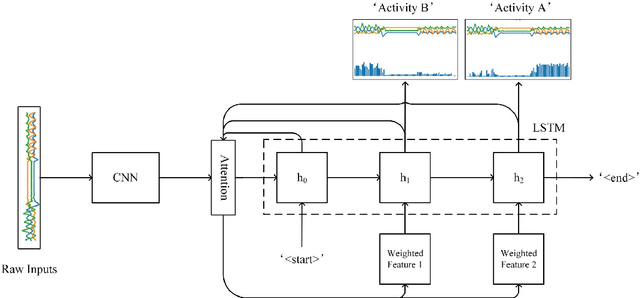
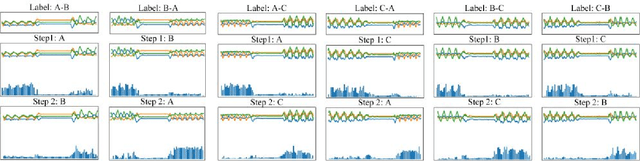
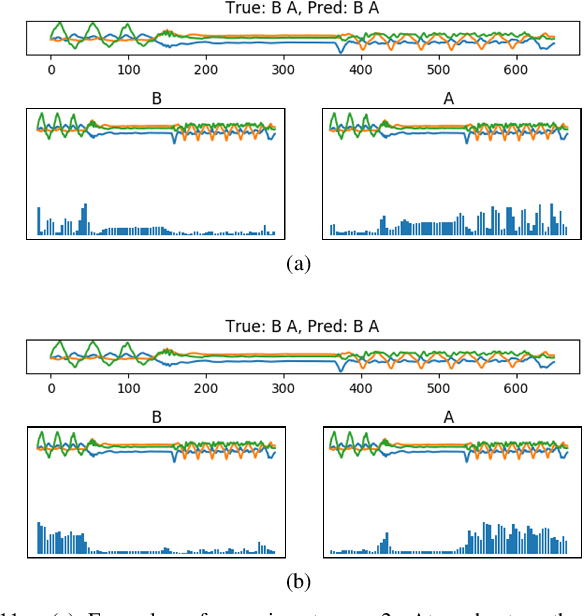
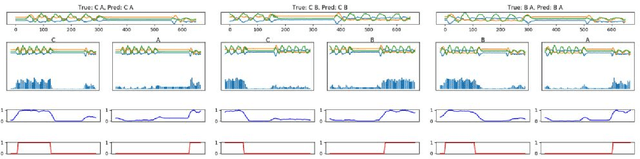
With the popularity and development of the wearable devices such as smartphones, human activity recognition (HAR) based on sensors has become as a key research area in human computer interaction and ubiquitous computing. The emergence of deep learning leads to a recent shift in the research of HAR, which requires massive strictly labeled data. In comparison with video data, activity data recorded from an accelerometer or gyroscope is often more difficult to interpret and segment. Recently, several attention mechanisms are proposed to handle the weakly labeled human activity data, which do not require accurate data annotation. However, these attention-based models can only handle the weakly labeled dataset whose segment includes one labeled activity, as a result it limits efficiency and practicality. In the paper, we proposed a recurrent attention network to handle sequential activity recognition and location tasks. The model can repeatedly perform steps of attention on multiple activities of one segment and each step is corresponding to the current focused activity according to its previous observations. The effectiveness of the recurrent attention model is validated by comparing with a baseline CNN, on the UniMiB-SHAR dataset and a collected sequential weakly labeled multi-activity dataset. The experiment results show that our recurrent attention model not only can perform single activity recognition tasks, but also can recognize and locate sequential weakly labeled multi-activity data. Besides, the recurrent attention can greatly facilitate the process of sensor data accumulation by automatically segmenting the regions of interest.

Exploitation and Exploration Analysis of Elitist Evolutionary Algorithms: A Case Study

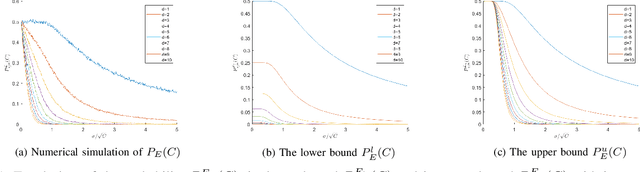
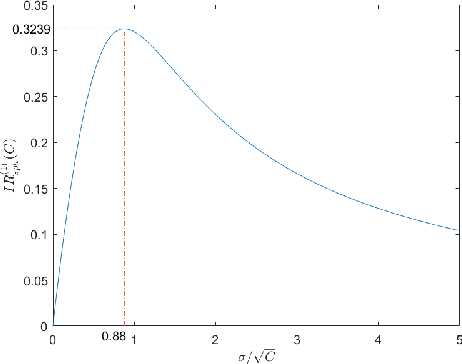
Known as two cornerstones of problem solving by search, exploitation and exploration are extensively discussed for implementation and application of evolutionary algorithms (EAs). However, only a few researches focus on evaluation and theoretical estimation of exploitation and exploration. Considering that exploitation and exploration are two issues regarding global search and local search, this paper proposes to evaluate them via the success probability and the one-step improvement rate computed in different domains of integration. Then, case studies are performed by analyzing performances of (1+1) random univariate search and (1+1) evolutionary programming on the sphere function and the cheating problem. By rigorous theoretical analysis, we demonstrate that both exploitation and exploration of the investigated elitist EAs degenerate exponentially with the problem dimension $n$. Meanwhile, it is also shown that maximization of exploitation and exploration can be achieved by setting an appropriate value for the standard deviation $\sigma$ of Gaussian mutation, which is positively related to the distance from the present solution to the center of the promising region.

Conditionally Learn to Pay Attention for Sequential Visual Task

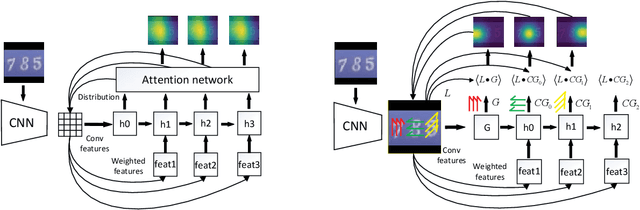
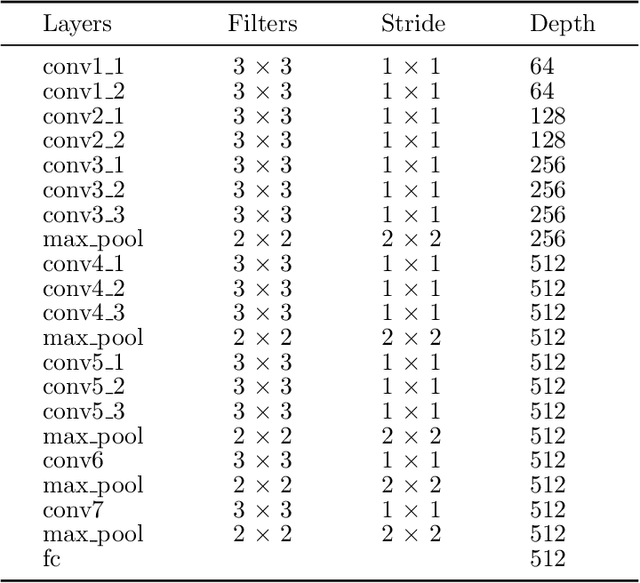
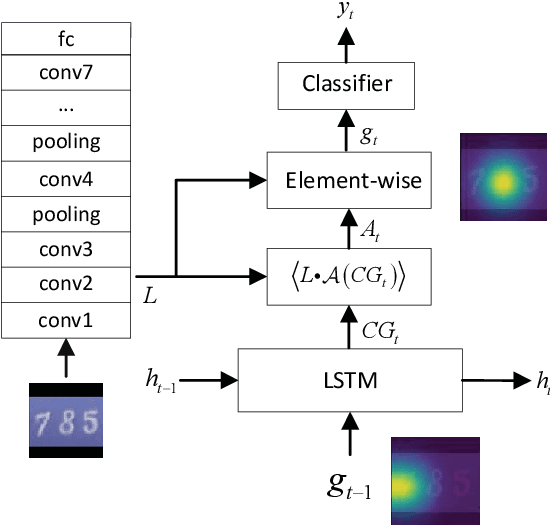
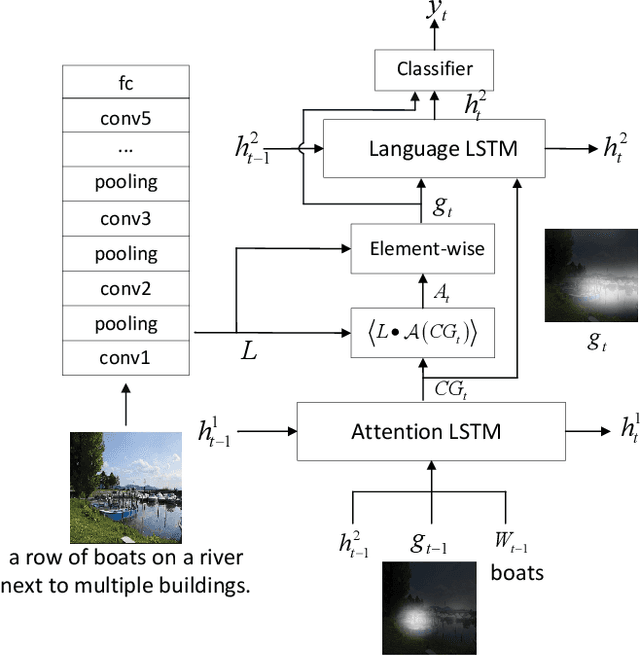
Sequential visual task usually requires to pay attention to its current interested object conditional on its previous observations. Different from popular soft attention mechanism, we propose a new attention framework by introducing a novel conditional global feature which represents the weak feature descriptor of the current focused object. Specifically, for a standard CNN (Convolutional Neural Network) pipeline, the convolutional layers with different receptive fields are used to produce the attention maps by measuring how the convolutional features align to the conditional global feature. The conditional global feature can be generated by different recurrent structure according to different visual tasks, such as a simple recurrent neural network for multiple objects recognition, or a moderate complex language model for image caption. Experiments show that our proposed conditional attention model achieves the best performance on the SVHN (Street View House Numbers) dataset with / without extra bounding box; and for image caption, our attention model generates better scores than the popular soft attention model.

Estimating Approximation Errors of Elitist Evolutionary Algorithms

When evolutionary algorithms (EAs) are unlikely to locate precise global optimal solutions with satisfactory performances, it is important to substitute alternative theoretical routine for the analysis of hitting time/running time. In order to narrow the gap between theories and applications, this paper is dedicated to perform an analysis on approximation error of EAs. First, we proposed a general result on upper bound and lower bound of approximation errors. Then, several case studies are performed to present the routine of error analysis, and theoretical results show the close connections between approximation errors and eigenvalues of transition matrices. The analysis validates applicability of error analysis, demonstrates significance of estimation results, and then, exhibits its potential to be applied for theoretical analysis of elitist EAs.

Unlimited Budget Analysis of Randomised Search Heuristics

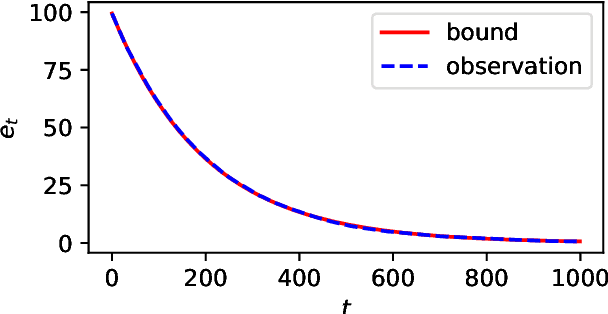
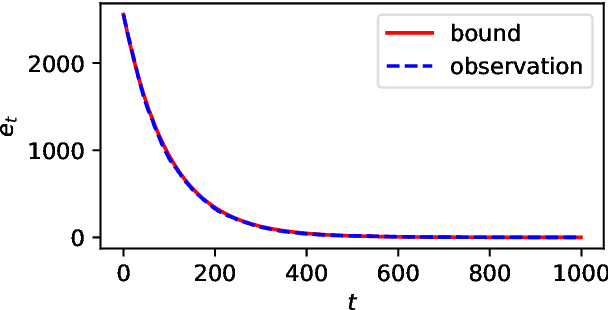
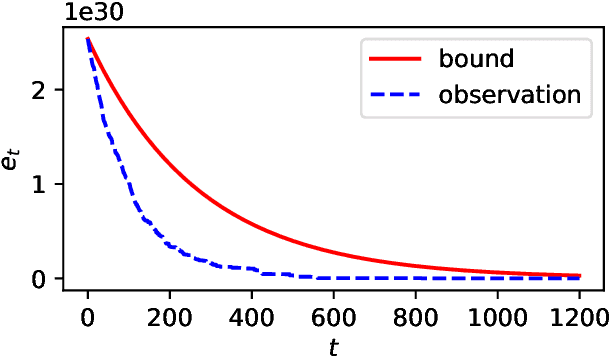
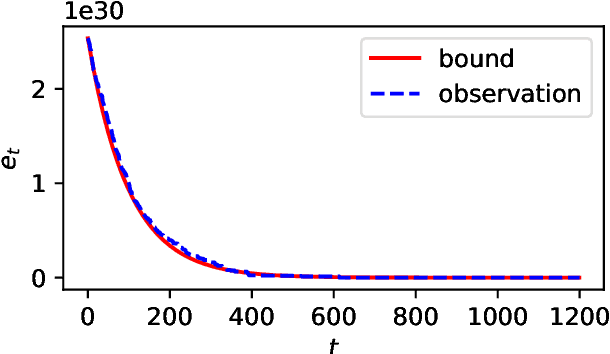
Performance analysis of all kinds of randomised search heuristics is a rapidly growing and developing field. Run time and solution quality are two popular measures of the performance of these algorithms. The focus of this paper is on the solution quality an optimisation heuristic achieves, not on the time it takes to reach this goal, setting it far apart from runtime analysis. We contribute to its further development by introducing a novel analytical framework, called unlimited budget analysis, to derive the expected fitness value after arbitrary computational steps. It has its roots in the very recently introduced approximation error analysis and bears some similarity to fixed budget analysis. We present the framework, apply it to simple mutation-based algorithms, covering both, local and global search. We provide analytical results for a number of pseudo-Boolean functions for unlimited budget analysis and compare them to results derived within the fixed budget framework for the same algorithms and functions. There are also results of experiments to compare bounds obtained in the two different frameworks with the actual observed performance. The study show that unlimited budget analysis may lead to the same or more general estimation beyond fixed budget.

Attention-based Convolutional Neural Network for Weakly Labeled Human Activities Recognition with Wearable Sensors

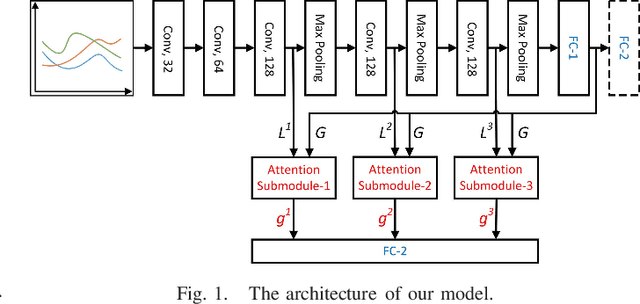
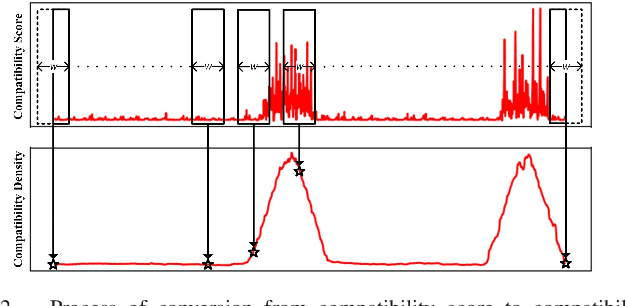
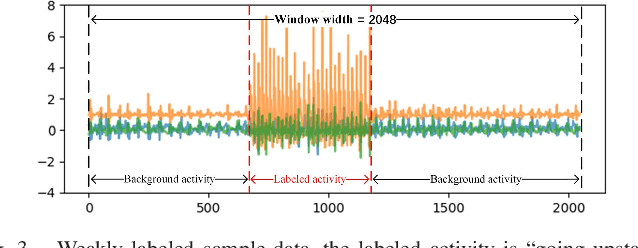
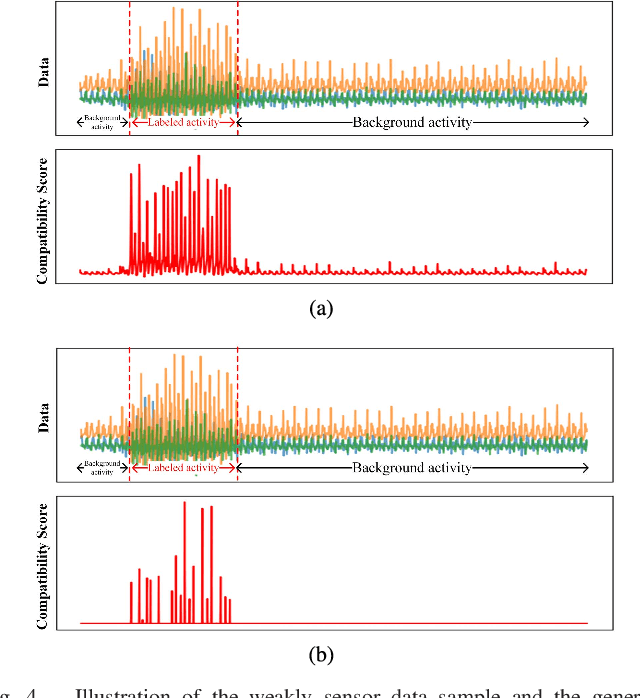
Unlike images or videos data which can be easily labeled by human being, sensor data annotation is a time-consuming process. However, traditional methods of human activity recognition require a large amount of such strictly labeled data for training classifiers. In this paper, we present an attention-based convolutional neural network for human recognition from weakly labeled data. The proposed attention model can focus on labeled activity among a long sequence of sensor data, and while filter out a large amount of background noise signals. In experiment on the weakly labeled dataset, we show that our attention model outperforms classical deep learning methods in accuracy. Besides, we determine the specific locations of the labeled activity in a long sequence of weakly labeled data by converting the compatibility score which is generated from attention model to compatibility density. Our method greatly facilitates the process of sensor data annotation, and makes data collection more easy.