Regret Bounds for Noise-Free Cascaded Kernelized Bandits

We consider optimizing a function network in the noise-free grey-box setting with RKHS function classes, where the exact intermediate results are observable. We assume that the structure of the network is known (but not the underlying functions comprising it), and we study three types of structures: (1) chain: a cascade of scalar-valued functions, (2) multi-output chain: a cascade of vector-valued functions, and (3) feed-forward network: a fully connected feed-forward network of scalar-valued functions. We propose a sequential upper confidence bound based algorithm GPN-UCB along with a general theoretical upper bound on the cumulative regret. For the Mat\'ern kernel, we additionally propose a non-adaptive sampling based method along with its theoretical upper bound on the simple regret. We also provide algorithm-independent lower bounds on the simple regret and cumulative regret, showing that GPN-UCB is near-optimal for chains and multi-output chains in broad cases of interest.

Benefits of Monotonicity in Safe Exploration with Gaussian Processes

We consider the problem of sequentially maximising an unknown function over a set of actions while ensuring that every sampled point has a function value below a given safety threshold. We model the function using kernel-based and Gaussian process methods, while differing from previous works in our assumption that the function is monotonically increasing with respect to a safety variable. This assumption is motivated by various practical applications such as adaptive clinical trial design and robotics. Taking inspiration from the GP-UCB and SafeOpt algorithms, we propose an algorithm, monotone safe UCB (M-SafeUCB) for this task. We show that M-SafeUCB enjoys theoretical guarantees in terms of safety, a suitably-defined regret notion, and approximately finding the entire safe boundary. In addition, we illustrate that the monotonicity assumption yields significant benefits in terms of both the guarantees obtained and the algorithmic simplicity. We support our theoretical findings by performing empirical evaluations on a variety of functions.

Max-Quantile Grouped Infinite-Arm Bandits

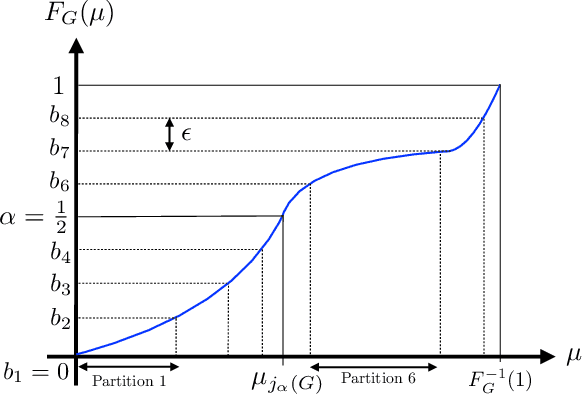
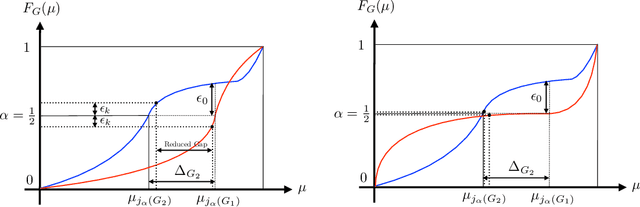
In this paper, we consider a bandit problem in which there are a number of groups each consisting of infinitely many arms. Whenever a new arm is requested from a given group, its mean reward is drawn from an unknown reservoir distribution (different for each group), and the uncertainty in the arm's mean reward can only be reduced via subsequent pulls of the arm. The goal is to identify the infinite-arm group whose reservoir distribution has the highest $(1-\alpha)$-quantile (e.g., median if $\alpha = \frac{1}{2}$), using as few total arm pulls as possible. We introduce a two-step algorithm that first requests a fixed number of arms from each group and then runs a finite-arm grouped max-quantile bandit algorithm. We characterize both the instance-dependent and worst-case regret, and provide a matching lower bound for the latter, while discussing various strengths, weaknesses, algorithmic improvements, and potential lower bounds associated with our instance-dependent upper bounds.

Theoretical Perspectives on Deep Learning Methods in Inverse Problems

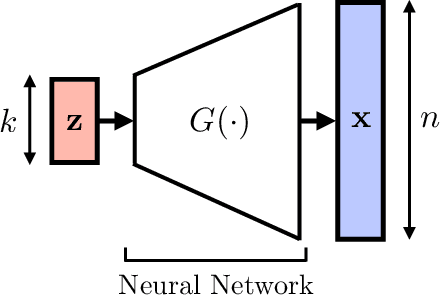
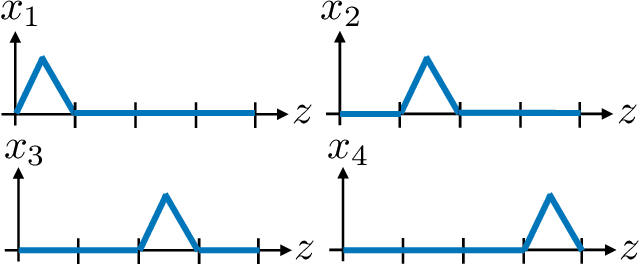
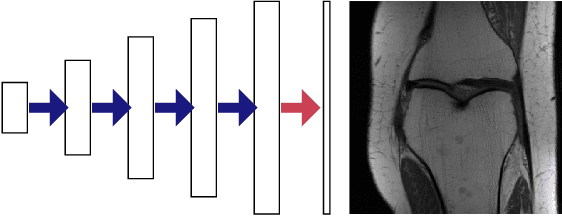
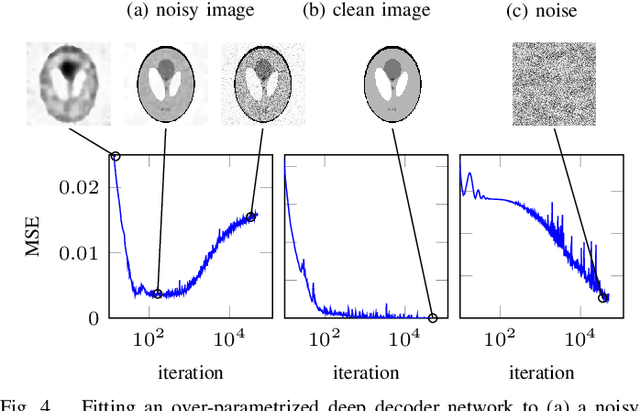
In recent years, there have been significant advances in the use of deep learning methods in inverse problems such as denoising, compressive sensing, inpainting, and super-resolution. While this line of works has predominantly been driven by practical algorithms and experiments, it has also given rise to a variety of intriguing theoretical problems. In this paper, we survey some of the prominent theoretical developments in this line of works, focusing in particular on generative priors, untrained neural network priors, and unfolding algorithms. In addition to summarizing existing results in these topics, we highlight several ongoing challenges and open problems.

Model-Based and Graph-Based Priors for Group Testing

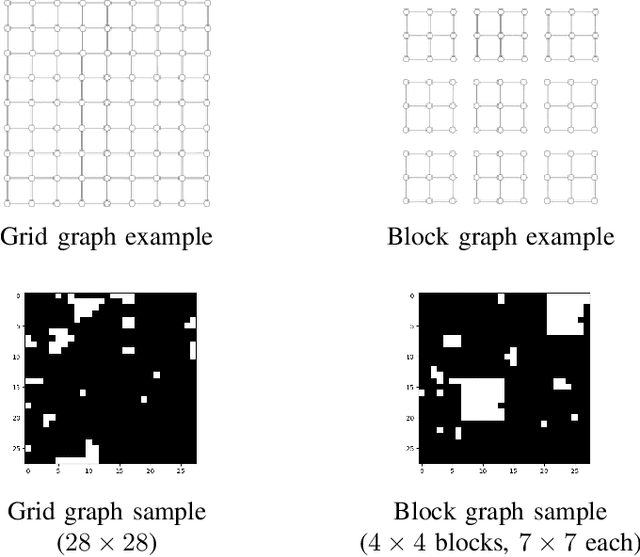
The goal of the group testing problem is to identify a set of defective items within a larger set of items, using suitably-designed tests whose outcomes indicate whether any defective item is present. In this paper, we study how the number of tests can be significantly decreased by leveraging the structural dependencies between the items, i.e., by incorporating prior information. To do so, we pursue two different perspectives: (i) As a generalization of the uniform combinatorial prior, we consider the case that the defective set is uniform over a \emph{subset} of all possible sets of a given size, and study how this impacts the information-theoretic limits on the number of tests for approximate recovery; (ii) As a generalization of the i.i.d.~prior, we introduce a new class of priors based on the Ising model, where the associated graph represents interactions between items. We show that this naturally leads to an Integer Quadratic Program decoder, which can be converted to an Integer Linear Program and/or relaxed to a non-integer variant for improved computational complexity, while maintaining strong empirical recovery performance.

Generative Principal Component Analysis

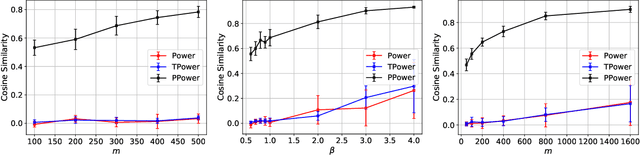
In this paper, we study the problem of principal component analysis with generative modeling assumptions, adopting a general model for the observed matrix that encompasses notable special cases, including spiked matrix recovery and phase retrieval. The key assumption is that the underlying signal lies near the range of an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs. We propose a quadratic estimator, and show that it enjoys a statistical rate of order $\sqrt{\frac{k\log L}{m}}$, where $m$ is the number of samples. We also provide a near-matching algorithm-independent lower bound. Moreover, we provide a variant of the classic power method, which projects the calculated data onto the range of the generative model during each iteration. We show that under suitable conditions, this method converges exponentially fast to a point achieving the above-mentioned statistical rate. We perform experiments on various image datasets for spiked matrix and phase retrieval models, and illustrate performance gains of our method to the classic power method and the truncated power method devised for sparse principal component analysis.

Order-Optimal Error Bounds for Noisy Kernel-Based Bayesian Quadrature

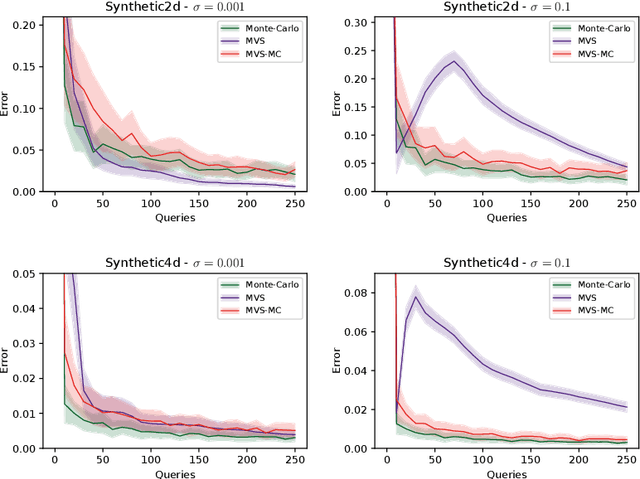
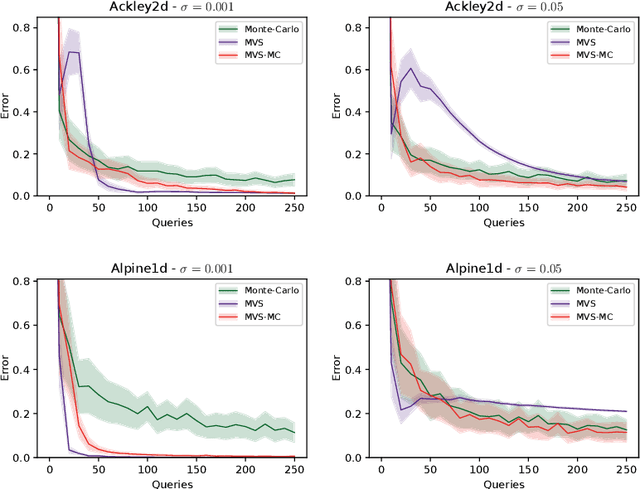
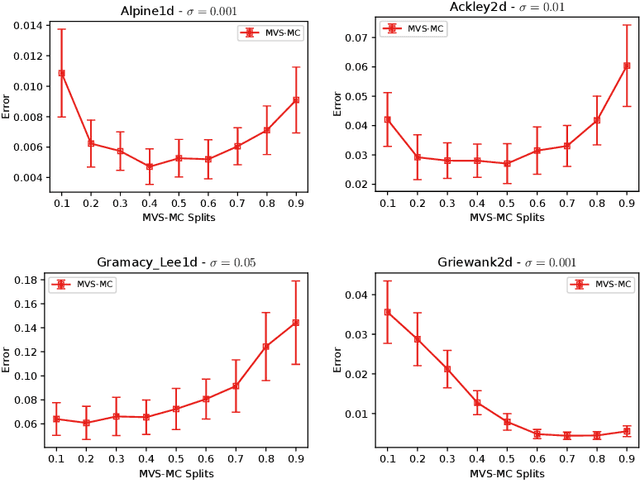
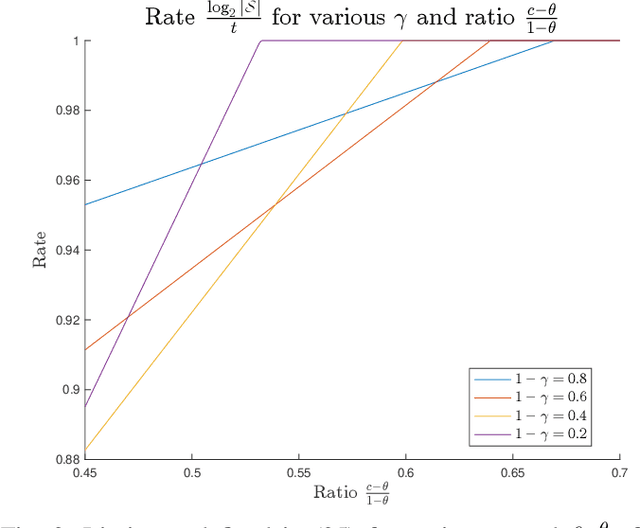
In this paper, we study the sample complexity of {\em noisy Bayesian quadrature} (BQ), in which we seek to approximate an integral based on noisy black-box queries to the underlying function. We consider functions in a {\em Reproducing Kernel Hilbert Space} (RKHS) with the Mat\'ern-$\nu$ kernel, focusing on combinations of the parameter $\nu$ and dimension $d$ such that the RKHS is equivalent to a Sobolev class. In this setting, we provide near-matching upper and lower bounds on the best possible average error. Specifically, we find that when the black-box queries are subject to Gaussian noise having variance $\sigma^2$, any algorithm making at most $T$ queries (even with adaptive sampling) must incur a mean absolute error of $\Omega(T^{-\frac{\nu}{d}-1} + \sigma T^{-\frac{1}{2}})$, and there exists a non-adaptive algorithm attaining an error of at most $O(T^{-\frac{\nu}{d}-1} + \sigma T^{-\frac{1}{2}})$. Hence, the bounds are order-optimal, and establish that there is no adaptivity gap in terms of scaling laws.

Improved Convergence Rates for Sparse Approximation Methods in Kernel-Based Learning

Kernel-based models such as kernel ridge regression and Gaussian processes are ubiquitous in machine learning applications for regression and optimization. It is well known that a serious downside for kernel-based models is the high computational cost; given a dataset of $n$ samples, the cost grows as $\mathcal{O}(n^3)$. Existing sparse approximation methods can yield a significant reduction in the computational cost, effectively reducing the real world cost down to as low as $\mathcal{O}(n)$ in certain cases. Despite this remarkable empirical success, significant gaps remain in the existing results for the analytical confidence bounds on the error due to approximation. In this work, we provide novel confidence intervals for the Nystr\"om method and the sparse variational Gaussian processes approximation method. Our confidence intervals lead to improved error bounds in both regression and optimization. We establish these confidence intervals using novel interpretations of the approximate (surrogate) posterior variance of the models.

A Robust Phased Elimination Algorithm for Corruption-Tolerant Gaussian Process Bandits

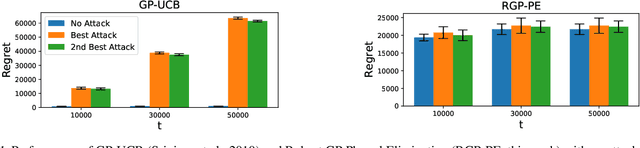
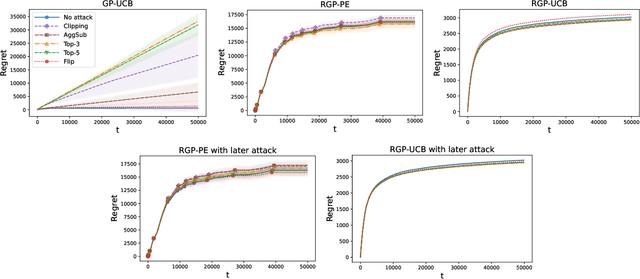
We consider the sequential optimization of an unknown, continuous, and expensive to evaluate reward function, from noisy and adversarially corrupted observed rewards. When the corruption attacks are subject to a suitable budget $C$ and the function lives in a Reproducing Kernel Hilbert Space (RKHS), the problem can be posed as corrupted Gaussian process (GP) bandit optimization. We propose a novel robust elimination-type algorithm that runs in epochs, combines exploration with infrequent switching to select a small subset of actions, and plays each action for multiple time instants. Our algorithm, Robust GP Phased Elimination (RGP-PE), successfully balances robustness to corruptions with exploration and exploitation such that its performance degrades minimally in the presence (or absence) of adversarial corruptions. When $T$ is the number of samples and $\gamma_T$ is the maximal information gain, the corruption-dependent term in our regret bound is $O(C \gamma_T^{3/2})$, which is significantly tighter than the existing $O(C \sqrt{T \gamma_T})$ for several commonly-considered kernels. We perform the first empirical study of robustness in the corrupted GP bandit setting, and show that our algorithm is robust against a variety of adversarial attacks.

Max-Min Grouped Bandits

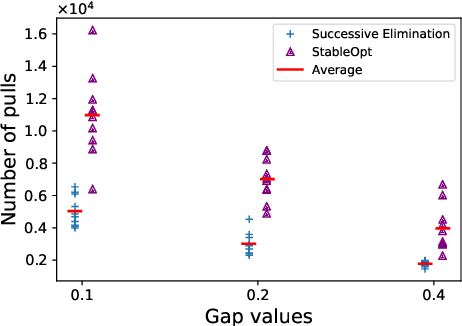
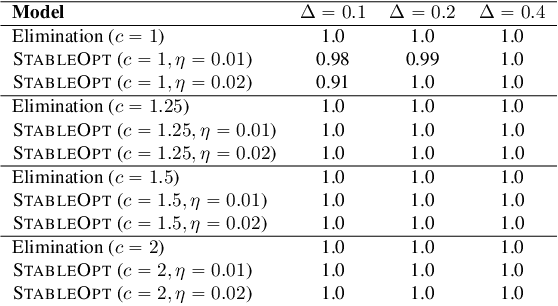
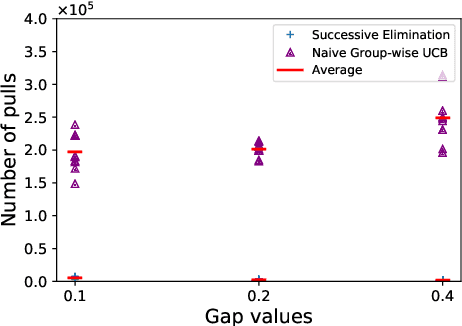
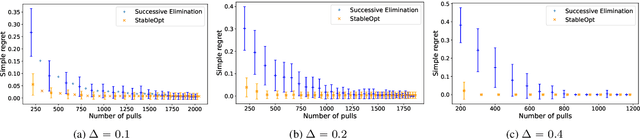
In this paper, we introduce a multi-armed bandit problem termed max-min grouped bandits, in which the arms are arranged in possibly-overlapping groups, and the goal is to find a group whose worst arm has the highest mean reward. This problem is of interest in applications such as recommendation systems, and is also closely related to widely-studied robust optimization problems. We present two algorithms based successive elimination and robust optimization, and derive upper bounds on the number of samples to guarantee finding a max-min optimal or near-optimal group, as well as an algorithm-independent lower bound. We discuss the degree of tightness of our bounds in various cases of interest, and the difficulties in deriving uniformly tight bounds.