The Joint Effect of Task Similarity and Overparameterization on Catastrophic Forgetting -- An Analytical Model

In continual learning, catastrophic forgetting is affected by multiple aspects of the tasks. Previous works have analyzed separately how forgetting is affected by either task similarity or overparameterization. In contrast, our paper examines how task similarity and overparameterization jointly affect forgetting in an analyzable model. Specifically, we focus on two-task continual linear regression, where the second task is a random orthogonal transformation of an arbitrary first task (an abstraction of random permutation tasks). We derive an exact analytical expression for the expected forgetting - and uncover a nuanced pattern. In highly overparameterized models, intermediate task similarity causes the most forgetting. However, near the interpolation threshold, forgetting decreases monotonically with the expected task similarity. We validate our findings with linear regression on synthetic data, and with neural networks on established permutation task benchmarks.

Theoretical Perspectives on Deep Learning Methods in Inverse Problems

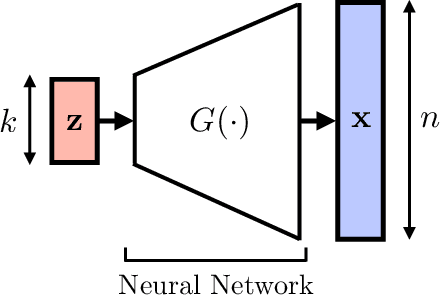
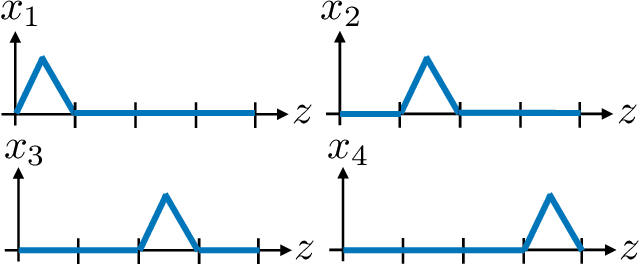
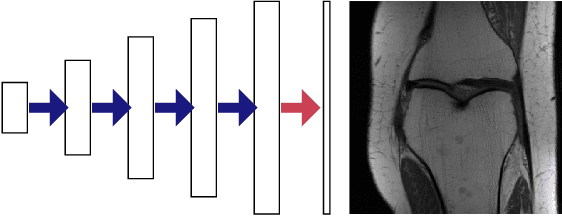
In recent years, there have been significant advances in the use of deep learning methods in inverse problems such as denoising, compressive sensing, inpainting, and super-resolution. While this line of works has predominantly been driven by practical algorithms and experiments, it has also given rise to a variety of intriguing theoretical problems. In this paper, we survey some of the prominent theoretical developments in this line of works, focusing in particular on generative priors, untrained neural network priors, and unfolding algorithms. In addition to summarizing existing results in these topics, we highlight several ongoing challenges and open problems.

Regularized Training of Intermediate Layers for Generative Models for Inverse Problems

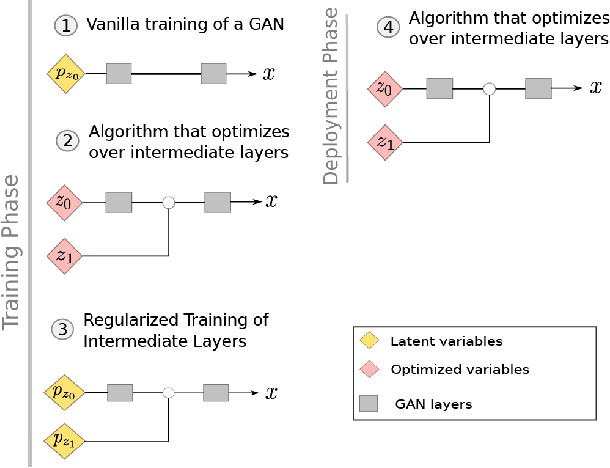
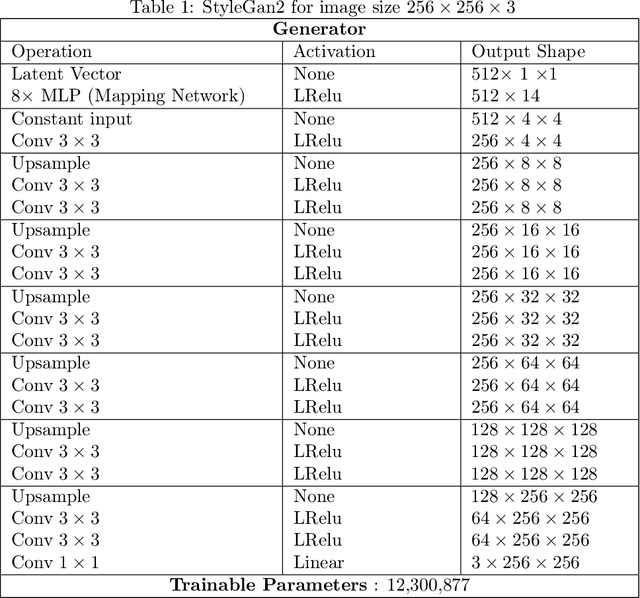
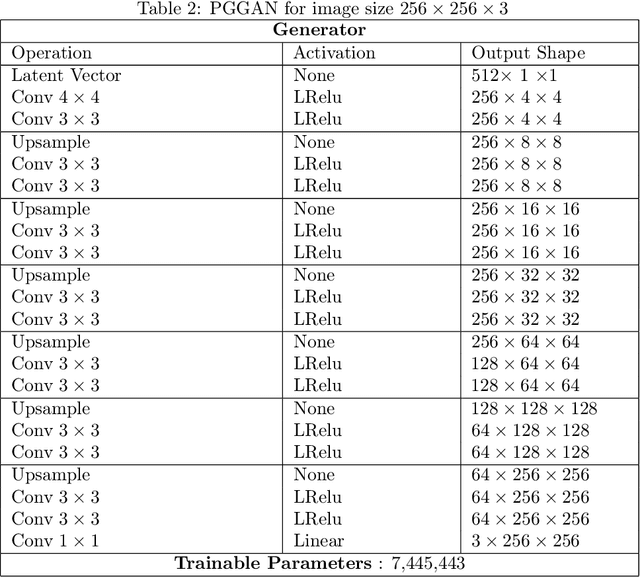
Generative Adversarial Networks (GANs) have been shown to be powerful and flexible priors when solving inverse problems. One challenge of using them is overcoming representation error, the fundamental limitation of the network in representing any particular signal. Recently, multiple proposed inversion algorithms reduce representation error by optimizing over intermediate layer representations. These methods are typically applied to generative models that were trained agnostic of the downstream inversion algorithm. In our work, we introduce a principle that if a generative model is intended for inversion using an algorithm based on optimization of intermediate layers, it should be trained in a way that regularizes those intermediate layers. We instantiate this principle for two notable recent inversion algorithms: Intermediate Layer Optimization and the Multi-Code GAN prior. For both of these inversion algorithms, we introduce a new regularized GAN training algorithm and demonstrate that the learned generative model results in lower reconstruction errors across a wide range of under sampling ratios when solving compressed sensing, inpainting, and super-resolution problems.

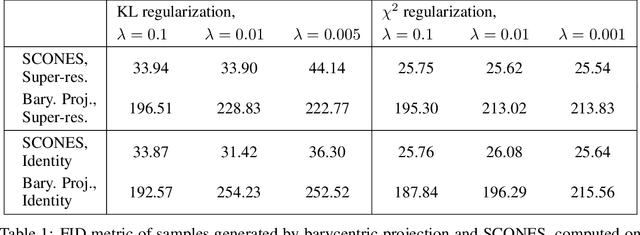
Score-based Generative Neural Networks for Large-Scale Optimal Transport

We consider the fundamental problem of sampling the optimal transport coupling between given source and target distributions. In certain cases, the optimal transport plan takes the form of a one-to-one mapping from the source support to the target support, but learning or even approximating such a map is computationally challenging for large and high-dimensional datasets due to the high cost of linear programming routines and an intrinsic curse of dimensionality. We study instead the Sinkhorn problem, a regularized form of optimal transport whose solutions are couplings between the source and the target distribution. We introduce a novel framework for learning the Sinkhorn coupling between two distributions in the form of a score-based generative model. Conditioned on source data, our procedure iterates Langevin Dynamics to sample target data according to the regularized optimal coupling. Key to this approach is a neural network parametrization of the Sinkhorn problem, and we prove convergence of gradient descent with respect to network parameters in this formulation. We demonstrate its empirical success on a variety of large scale optimal transport tasks.

Generator Surgery for Compressed Sensing

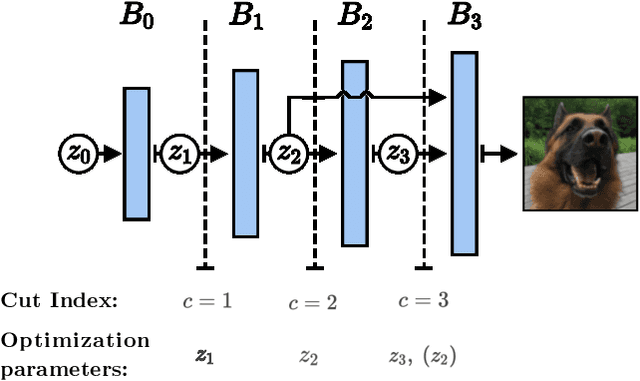
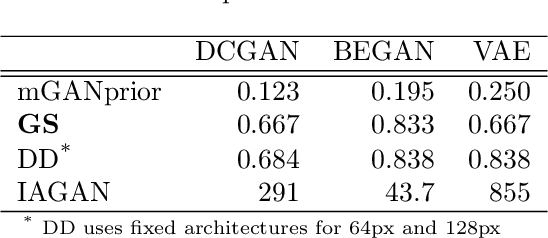
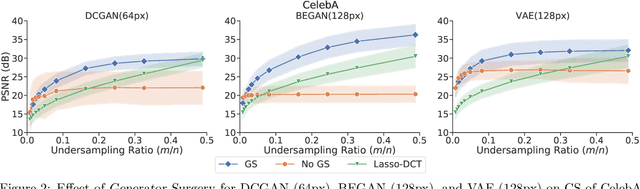
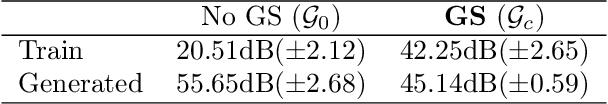
Image recovery from compressive measurements requires a signal prior for the images being reconstructed. Recent work has explored the use of deep generative models with low latent dimension as signal priors for such problems. However, their recovery performance is limited by high representation error. We introduce a method for achieving low representation error using generators as signal priors. Using a pre-trained generator, we remove one or more initial blocks at test time and optimize over the new, higher-dimensional latent space to recover a target image. Experiments demonstrate significantly improved reconstruction quality for a variety of network architectures. This approach also works well for out-of-training-distribution images and is competitive with other state-of-the-art methods. Our experiments show that test-time architectural modifications can greatly improve the recovery quality of generator signal priors for compressed sensing.

Optimal Sample Complexity of Gradient Descent for Amplitude Flow via Non-Lipschitz Matrix Concentration

We consider the problem of recovering a real-valued $n$-dimensional signal from $m$ phaseless, linear measurements and analyze the amplitude-based non-smooth least squares objective. We establish local convergence of gradient descent with optimal sample complexity based on the uniform concentration of a random, discontinuous matrix-valued operator arising from the objective's gradient dynamics. While common techniques to establish uniform concentration of random functions exploit Lipschitz continuity, we prove that the discontinuous matrix-valued operator satisfies a uniform matrix concentration inequality when the measurement vectors are Gaussian as soon as $m = \Omega(n)$ with high probability. We then show that satisfaction of this inequality is sufficient for gradient descent with proper initialization to converge linearly to the true solution up to the global sign ambiguity. As a consequence, this guarantees local convergence for Gaussian measurements at optimal sample complexity. The concentration methods in the present work have previously been used to establish recovery guarantees for a variety of inverse problems under generative neural network priors. This paper demonstrates the applicability of these techniques to more traditional inverse problems and serves as a pedagogical introduction to those results.

Compressive Phase Retrieval: Optimal Sample Complexity with Deep Generative Priors

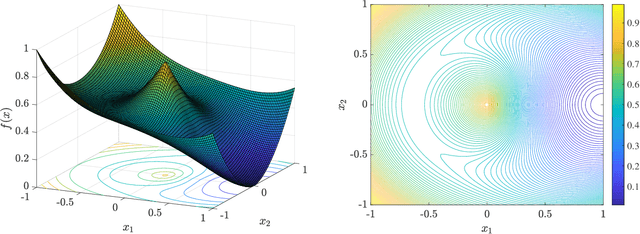
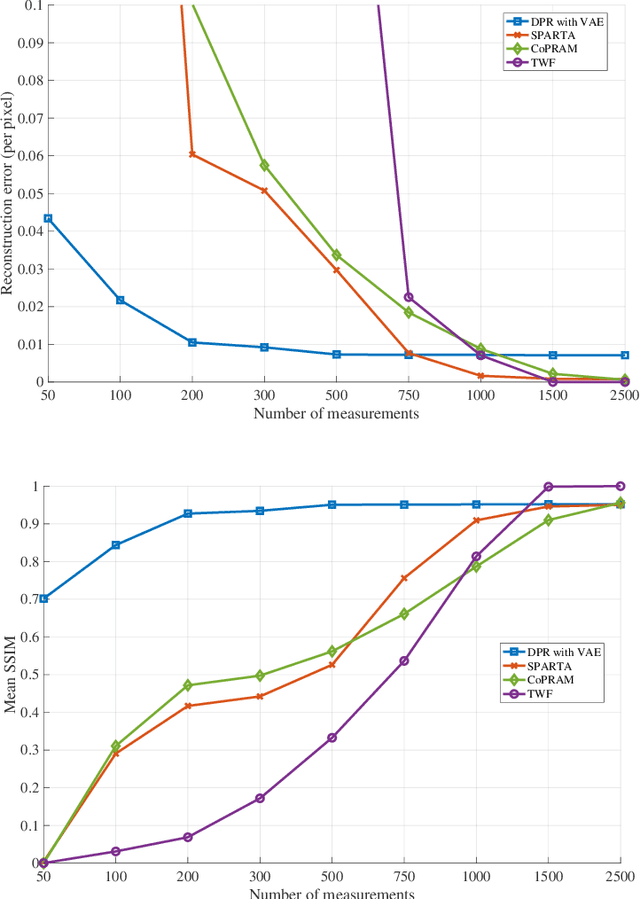
Advances in compressive sensing provided reconstruction algorithms of sparse signals from linear measurements with optimal sample complexity, but natural extensions of this methodology to nonlinear inverse problems have been met with potentially fundamental sample complexity bottlenecks. In particular, tractable algorithms for compressive phase retrieval with sparsity priors have not been able to achieve optimal sample complexity. This has created an open problem in compressive phase retrieval: under generic, phaseless linear measurements, are there tractable reconstruction algorithms that succeed with optimal sample complexity? Meanwhile, progress in machine learning has led to the development of new data-driven signal priors in the form of generative models, which can outperform sparsity priors with significantly fewer measurements. In this work, we resolve the open problem in compressive phase retrieval and demonstrate that generative priors can lead to a fundamental advance by permitting optimal sample complexity by a tractable algorithm in this challenging nonlinear inverse problem. We additionally provide empirics showing that exploiting generative priors in phase retrieval can significantly outperform sparsity priors. These results provide support for generative priors as a new paradigm for signal recovery in a variety of contexts, both empirically and theoretically. The strengths of this paradigm are that (1) generative priors can represent some classes of natural signals more concisely than sparsity priors, (2) generative priors allow for direct optimization over the natural signal manifold, which is intractable under sparsity priors, and (3) the resulting non-convex optimization problems with generative priors can admit benign optimization landscapes at optimal sample complexity, perhaps surprisingly, even in cases of nonlinear measurements.

Nonasymptotic Guarantees for Low-Rank Matrix Recovery with Generative Priors

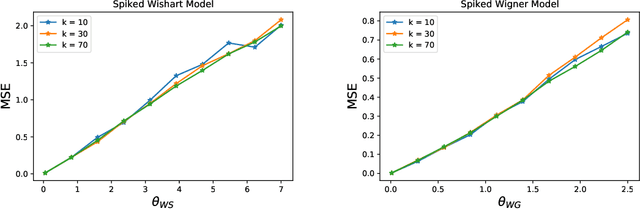
Many problems in statistics and machine learning require the reconstruction of a low-rank signal matrix from noisy data. Enforcing additional prior information on the low-rank component is often key to guaranteeing good recovery performance. One such prior on the low-rank component is sparsity, giving rise to the sparse principal component analysis problem. Unfortunately, this problem suffers from a computational-to-statistical gap, which may be fundamental. In this work, we study an alternative prior where the low-rank component is in the range of a trained generative network. We provide a non-asymptotic analysis with optimal sample complexity, up to logarithmic factors, for low-rank matrix recovery under an expansive-Gaussian network prior. Specifically, we establish a favorable global optimization landscape for a mean squared error optimization, provided the number of samples is on the order of the dimensionality of the input to the generative model. As a result, we establish that generative priors have no computational-to-statistical gap for structured low-rank matrix recovery in the finite data, nonasymptotic regime. We present this analysis in the case of both the Wishart and Wigner spiked matrix models.

Global Convergence of Sobolev Training for Overparametrized Neural Networks

Sobolev loss is used when training a network to approximate the values and derivatives of a target function at a prescribed set of input points. Recent works have demonstrated its successful applications in various tasks such as distillation or synthetic gradient prediction. In this work we prove that an overparametrized two-layer relu neural network trained on the Sobolev loss with gradient flow from random initialization can fit any given function values and any given directional derivatives, under a separation condition on the input data.

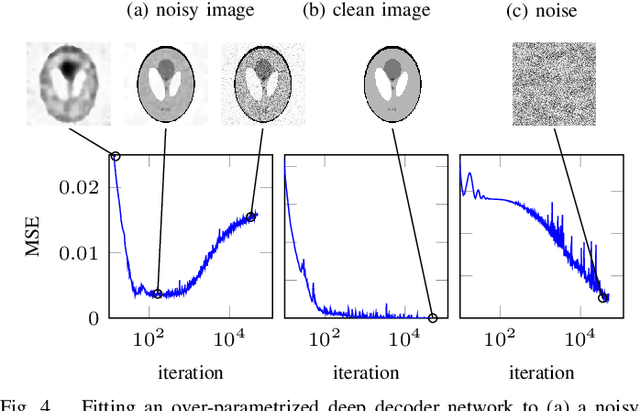
Reducing the Representation Error of GAN Image Priors Using the Deep Decoder

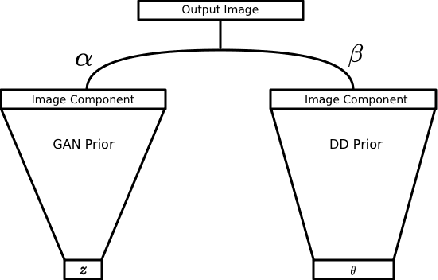
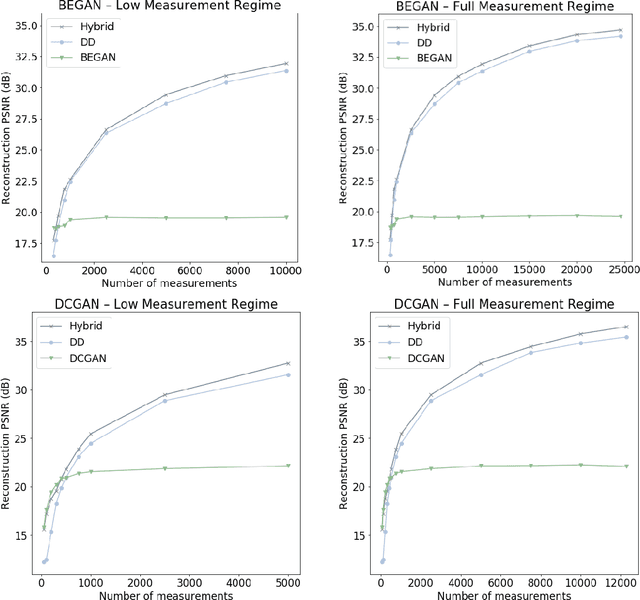
Generative models, such as GANs, learn an explicit low-dimensional representation of a particular class of images, and so they may be used as natural image priors for solving inverse problems such as image restoration and compressive sensing. GAN priors have demonstrated impressive performance on these tasks, but they can exhibit substantial representation error for both in-distribution and out-of-distribution images, because of the mismatch between the learned, approximate image distribution and the data generating distribution. In this paper, we demonstrate a method for reducing the representation error of GAN priors by modeling images as the linear combination of a GAN prior with a Deep Decoder. The deep decoder is an underparameterized and most importantly unlearned natural signal model similar to the Deep Image Prior. No knowledge of the specific inverse problem is needed in the training of the GAN underlying our method. For compressive sensing and image superresolution, our hybrid model exhibits consistently higher PSNRs than both the GAN priors and Deep Decoder separately, both on in-distribution and out-of-distribution images. This model provides a method for extensibly and cheaply leveraging both the benefits of learned and unlearned image recovery priors in inverse problems.