Ivan Lau
Sequential 1-bit Mean Estimation with Near-Optimal Sample Complexity
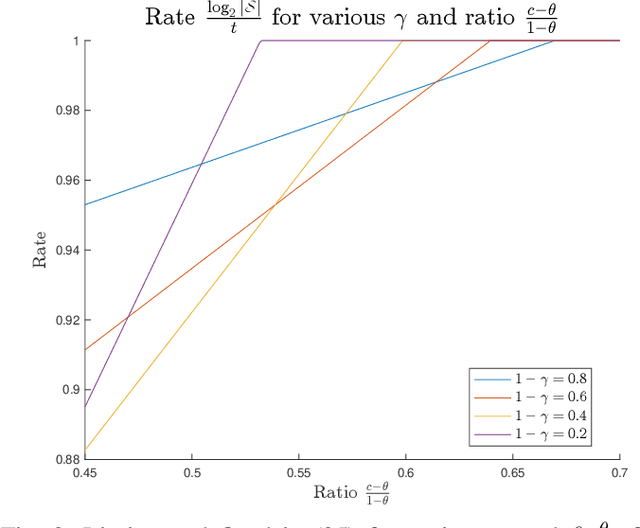
Sep 26, 2025Abstract:In this paper, we study the problem of distributed mean estimation with 1-bit communication constraints. We propose a mean estimator that is based on (randomized and sequentially-chosen) interval queries, whose 1-bit outcome indicates whether the given sample lies in the specified interval. Our estimator is $(\epsilon, \delta)$-PAC for all distributions with bounded mean ($-\lambda \le \mathbb{E}(X) \le \lambda $) and variance ($\mathrm{Var}(X) \le \sigma^2$) for some known parameters $\lambda$ and $\sigma$. We derive a sample complexity bound $\widetilde{O}\big( \frac{\sigma^2}{\epsilon^2}\log\frac{1}{\delta} + \log\frac{\lambda}{\sigma}\big)$, which matches the minimax lower bound for the unquantized setting up to logarithmic factors and the additional $\log\frac{\lambda}{\sigma}$ term that we show to be unavoidable. We also establish an adaptivity gap for interval-query based estimators: the best non-adaptive mean estimator is considerably worse than our adaptive mean estimator for large $\frac{\lambda}{\sigma}$. Finally, we give tightened sample complexity bounds for distributions with stronger tail decay, and present additional variants that (i) handle an unknown sampling budget (ii) adapt to the unknown true variance given (possibly loose) upper and lower bounds on the variance, and (iii) use only two stages of adaptivity at the expense of more complicated (non-interval) queries.
Quantile Multi-Armed Bandits with 1-bit Feedback
Feb 10, 2025Abstract:In this paper, we study a variant of best-arm identification involving elements of risk sensitivity and communication constraints. Specifically, the goal of the learner is to identify the arm with the highest quantile reward, while the communication from an agent (who observes rewards) and the learner (who chooses actions) is restricted to only one bit of feedback per arm pull. We propose an algorithm that utilizes noisy binary search as a subroutine, allowing the learner to estimate quantile rewards through 1-bit feedback. We derive an instance-dependent upper bound on the sample complexity of our algorithm and provide an algorithm-independent lower bound for specific instances, with the two matching to within logarithmic factors under mild conditions, or even to within constant factors in certain low error probability scaling regimes. The lower bound is applicable even in the absence of communication constraints, and thus we conclude that restricting to 1-bit feedback has a minimal impact on the scaling of the sample complexity.
Decentralized and Equitable Optimal Transport
Mar 12, 2024

Abstract:This paper considers the decentralized (discrete) optimal transport (D-OT) problem. In this setting, a network of agents seeks to design a transportation plan jointly, where the cost function is the sum of privately held costs for each agent. We reformulate the D-OT problem as a constraint-coupled optimization problem and propose a single-loop decentralized algorithm with an iteration complexity of O(1/{\epsilon}) that matches existing centralized first-order approaches. Moreover, we propose the decentralized equitable optimal transport (DE-OT) problem. In DE-OT, in addition to cooperatively designing a transportation plan that minimizes transportation costs, agents seek to ensure equity in their individual costs. The iteration complexity of the proposed method to solve DE-OT is also O(1/{\epsilon}). This rate improves existing centralized algorithms, where the best iteration complexity obtained is O(1/{\epsilon}^2).
Max-Quantile Grouped Infinite-Arm Bandits
Oct 04, 2022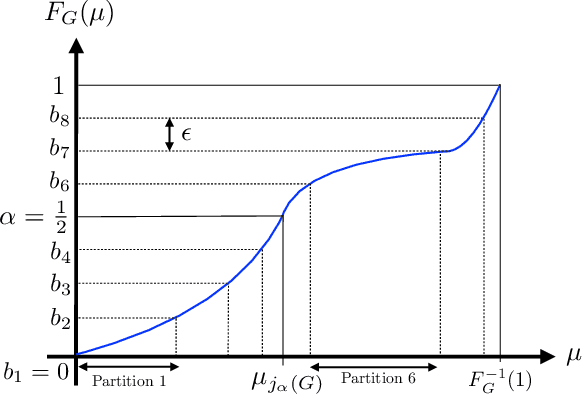
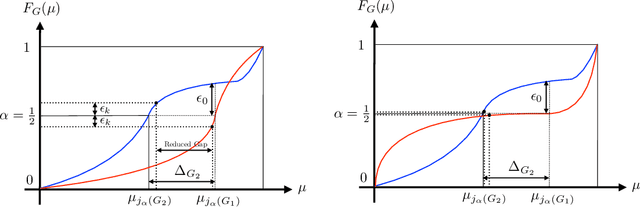
Abstract:In this paper, we consider a bandit problem in which there are a number of groups each consisting of infinitely many arms. Whenever a new arm is requested from a given group, its mean reward is drawn from an unknown reservoir distribution (different for each group), and the uncertainty in the arm's mean reward can only be reduced via subsequent pulls of the arm. The goal is to identify the infinite-arm group whose reservoir distribution has the highest $(1-\alpha)$-quantile (e.g., median if $\alpha = \frac{1}{2}$), using as few total arm pulls as possible. We introduce a two-step algorithm that first requests a fixed number of arms from each group and then runs a finite-arm grouped max-quantile bandit algorithm. We characterize both the instance-dependent and worst-case regret, and provide a matching lower bound for the latter, while discussing various strengths, weaknesses, algorithmic improvements, and potential lower bounds associated with our instance-dependent upper bounds.
Model-Based and Graph-Based Priors for Group Testing
May 24, 2022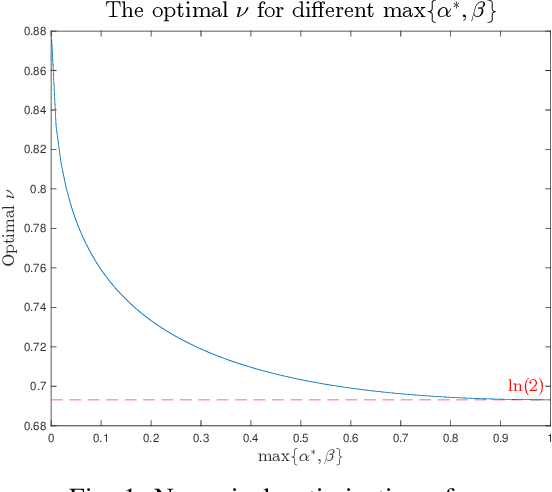
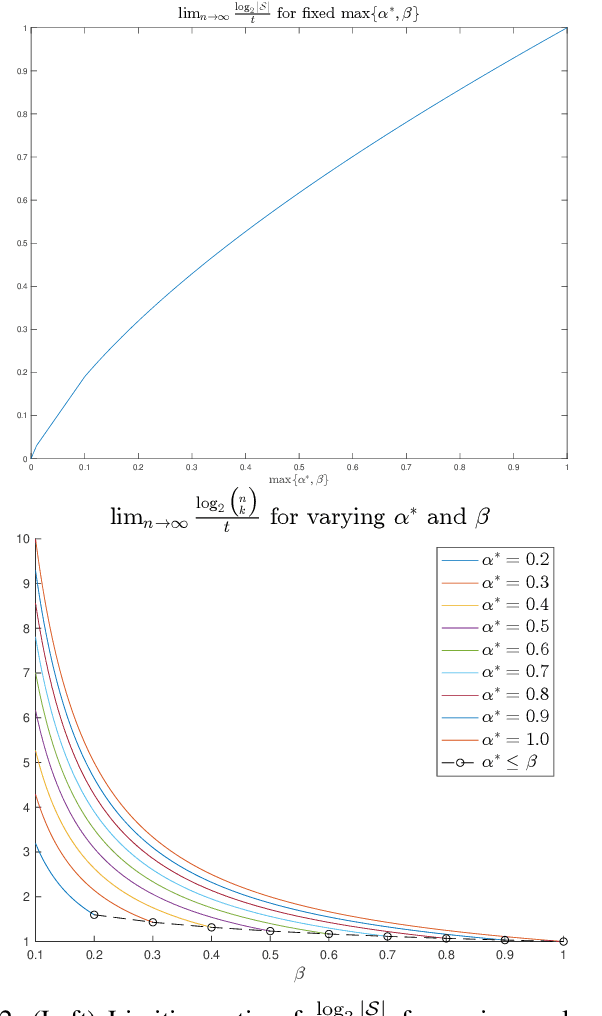
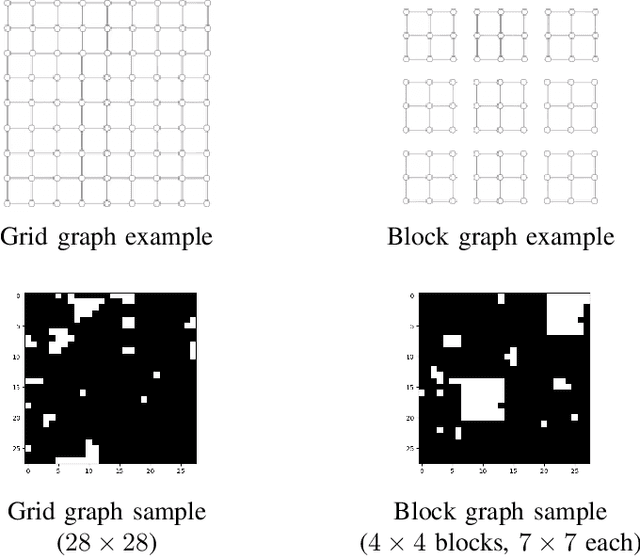
Abstract:The goal of the group testing problem is to identify a set of defective items within a larger set of items, using suitably-designed tests whose outcomes indicate whether any defective item is present. In this paper, we study how the number of tests can be significantly decreased by leveraging the structural dependencies between the items, i.e., by incorporating prior information. To do so, we pursue two different perspectives: (i) As a generalization of the uniform combinatorial prior, we consider the case that the defective set is uniform over a \emph{subset} of all possible sets of a given size, and study how this impacts the information-theoretic limits on the number of tests for approximate recovery; (ii) As a generalization of the i.i.d.~prior, we introduce a new class of priors based on the Ising model, where the associated graph represents interactions between items. We show that this naturally leads to an Integer Quadratic Program decoder, which can be converted to an Integer Linear Program and/or relaxed to a non-integer variant for improved computational complexity, while maintaining strong empirical recovery performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge