Envy-Free Allocation of Indivisible Goods via Noisy Queries

We introduce a problem of fairly allocating indivisible goods (items) in which the agents' valuations cannot be observed directly, but instead can only be accessed via noisy queries. In the two-agent setting with Gaussian noise and bounded valuations, we derive upper and lower bounds on the required number of queries for finding an envy-free allocation in terms of the number of items, $m$, and the negative-envy of the optimal allocation, $Δ$. In particular, when $Δ$ is not too small (namely, $Δ\gg m^{1/4}$), we establish that the optimal number of queries scales as $\frac{\sqrt m }{(Δ/ m)^2} = \frac{m^{2.5}}{Δ^2}$ up to logarithmic factors. Our upper bound is based on non-adaptive queries and a simple thresholding-based allocation algorithm that runs in polynomial time, while our lower bound holds even under adaptive queries and arbitrary computation time.

Statistical Mean Estimation with Coded Relayed Observations

We consider a problem of statistical mean estimation in which the samples are not observed directly, but are instead observed by a relay (``teacher'') that transmits information through a memoryless channel to the decoder (``student''), who then produces the final estimate. We consider the minimax estimation error in the large deviations regime, and establish achievable error exponents that are tight in broad regimes of the estimation accuracy and channel quality. In contrast, two natural baseline methods are shown to yield strictly suboptimal error exponents. We initially focus on Bernoulli sources and binary symmetric channels, and then generalize to sub-Gaussian and heavy-tailed settings along with arbitrary discrete memoryless channels.

Max-Quantile Grouped Infinite-Arm Bandits

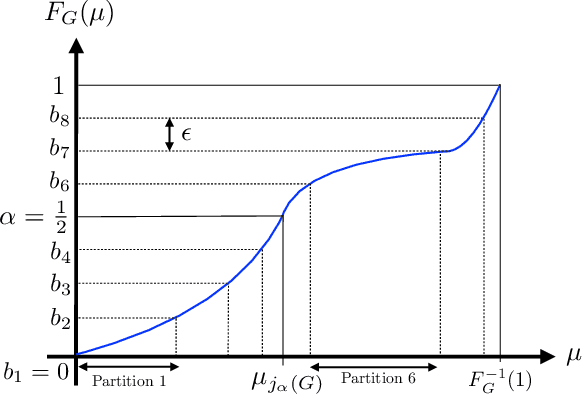
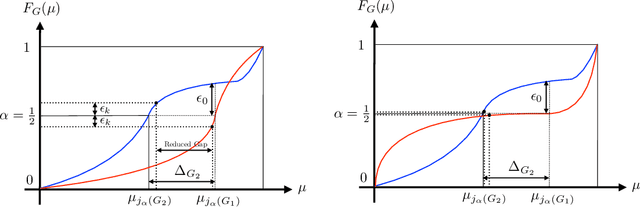
In this paper, we consider a bandit problem in which there are a number of groups each consisting of infinitely many arms. Whenever a new arm is requested from a given group, its mean reward is drawn from an unknown reservoir distribution (different for each group), and the uncertainty in the arm's mean reward can only be reduced via subsequent pulls of the arm. The goal is to identify the infinite-arm group whose reservoir distribution has the highest $(1-\alpha)$-quantile (e.g., median if $\alpha = \frac{1}{2}$), using as few total arm pulls as possible. We introduce a two-step algorithm that first requests a fixed number of arms from each group and then runs a finite-arm grouped max-quantile bandit algorithm. We characterize both the instance-dependent and worst-case regret, and provide a matching lower bound for the latter, while discussing various strengths, weaknesses, algorithmic improvements, and potential lower bounds associated with our instance-dependent upper bounds.