Location Dependent Dirichlet Processes

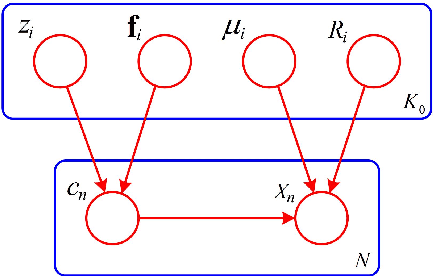
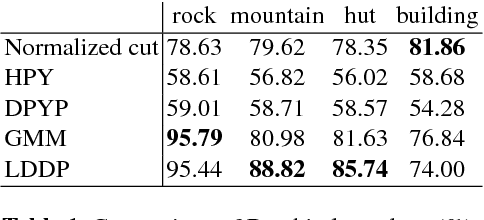
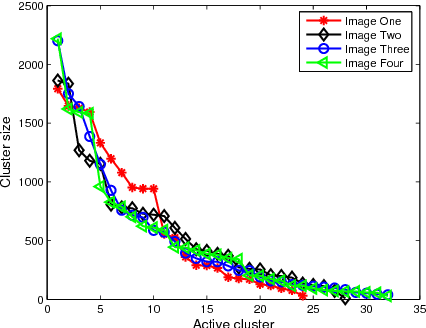
Dirichlet processes (DP) are widely applied in Bayesian nonparametric modeling. However, in their basic form they do not directly integrate dependency information among data arising from space and time. In this paper, we propose location dependent Dirichlet processes (LDDP) which incorporate nonparametric Gaussian processes in the DP modeling framework to model such dependencies. We develop the LDDP in the context of mixture modeling, and develop a mean field variational inference algorithm for this mixture model. The effectiveness of the proposed modeling framework is shown on an image segmentation task.

Nonlinear Kalman Filtering with Divergence Minimization

We consider the nonlinear Kalman filtering problem using Kullback-Leibler (KL) and $\alpha$-divergence measures as optimization criteria. Unlike linear Kalman filters, nonlinear Kalman filters do not have closed form Gaussian posteriors because of a lack of conjugacy due to the nonlinearity in the likelihood. In this paper we propose novel algorithms to optimize the forward and reverse forms of the KL divergence, as well as the alpha-divergence which contains these two as limiting cases. Unlike previous approaches, our algorithms do not make approximations to the divergences being optimized, but use Monte Carlo integration techniques to derive unbiased algorithms for direct optimization. We assess performance on radar and sensor tracking, and options pricing problems, showing general improvement over the UKF and EKF, as well as competitive performance with particle filtering.

TopicRNN: A Recurrent Neural Network with Long-Range Semantic Dependency

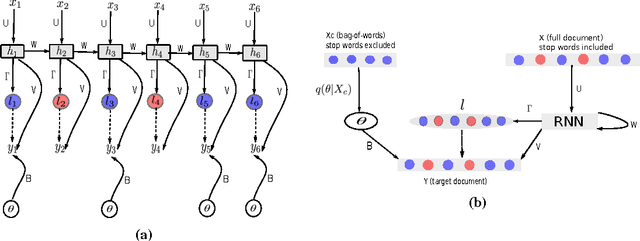
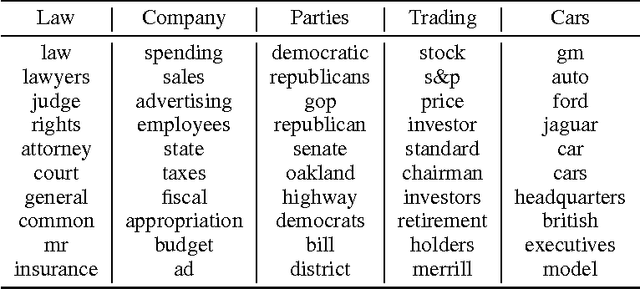
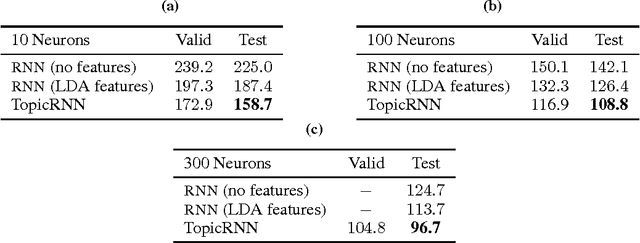
In this paper, we propose TopicRNN, a recurrent neural network (RNN)-based language model designed to directly capture the global semantic meaning relating words in a document via latent topics. Because of their sequential nature, RNNs are good at capturing the local structure of a word sequence - both semantic and syntactic - but might face difficulty remembering long-range dependencies. Intuitively, these long-range dependencies are of semantic nature. In contrast, latent topic models are able to capture the global underlying semantic structure of a document but do not account for word ordering. The proposed TopicRNN model integrates the merits of RNNs and latent topic models: it captures local (syntactic) dependencies using an RNN and global (semantic) dependencies using latent topics. Unlike previous work on contextual RNN language modeling, our model is learned end-to-end. Empirical results on word prediction show that TopicRNN outperforms existing contextual RNN baselines. In addition, TopicRNN can be used as an unsupervised feature extractor for documents. We do this for sentiment analysis on the IMDB movie review dataset and report an error rate of $6.28\%$. This is comparable to the state-of-the-art $5.91\%$ resulting from a semi-supervised approach. Finally, TopicRNN also yields sensible topics, making it a useful alternative to document models such as latent Dirichlet allocation.

Clearing the Skies: A deep network architecture for single-image rain removal

We introduce a deep network architecture called DerainNet for removing rain streaks from an image. Based on the deep convolutional neural network (CNN), we directly learn the mapping relationship between rainy and clean image detail layers from data. Because we do not possess the ground truth corresponding to real-world rainy images, we synthesize images with rain for training. In contrast to other common strategies that increase depth or breadth of the network, we use image processing domain knowledge to modify the objective function and improve deraining with a modestly-sized CNN. Specifically, we train our DerainNet on the detail (high-pass) layer rather than in the image domain. Though DerainNet is trained on synthetic data, we find that the learned network translates very effectively to real-world images for testing. Moreover, we augment the CNN framework with image enhancement to improve the visual results. Compared with state-of-the-art single image de-raining methods, our method has improved rain removal and much faster computation time after network training.

Bayesian Poisson Tensor Factorization for Inferring Multilateral Relations from Sparse Dyadic Event Counts

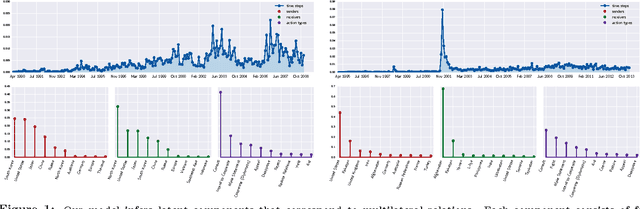
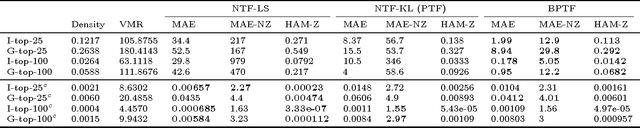
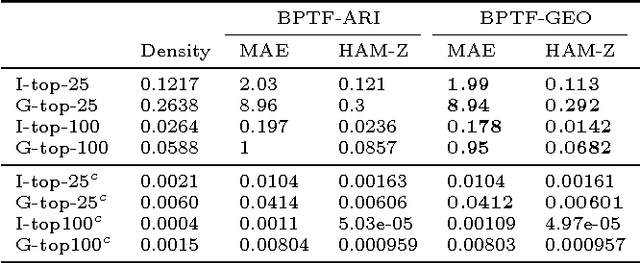
We present a Bayesian tensor factorization model for inferring latent group structures from dynamic pairwise interaction patterns. For decades, political scientists have collected and analyzed records of the form "country $i$ took action $a$ toward country $j$ at time $t$"---known as dyadic events---in order to form and test theories of international relations. We represent these event data as a tensor of counts and develop Bayesian Poisson tensor factorization to infer a low-dimensional, interpretable representation of their salient patterns. We demonstrate that our model's predictive performance is better than that of standard non-negative tensor factorization methods. We also provide a comparison of our variational updates to their maximum likelihood counterparts. In doing so, we identify a better way to form point estimates of the latent factors than that typically used in Bayesian Poisson matrix factorization. Finally, we showcase our model as an exploratory analysis tool for political scientists. We show that the inferred latent factor matrices capture interpretable multilateral relations that both conform to and inform our knowledge of international affairs.

Stochastic Annealing for Variational Inference

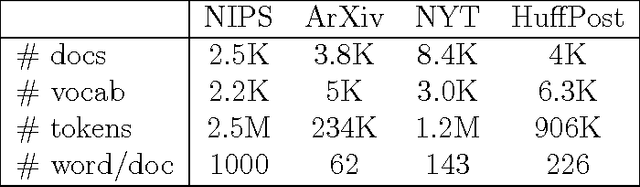
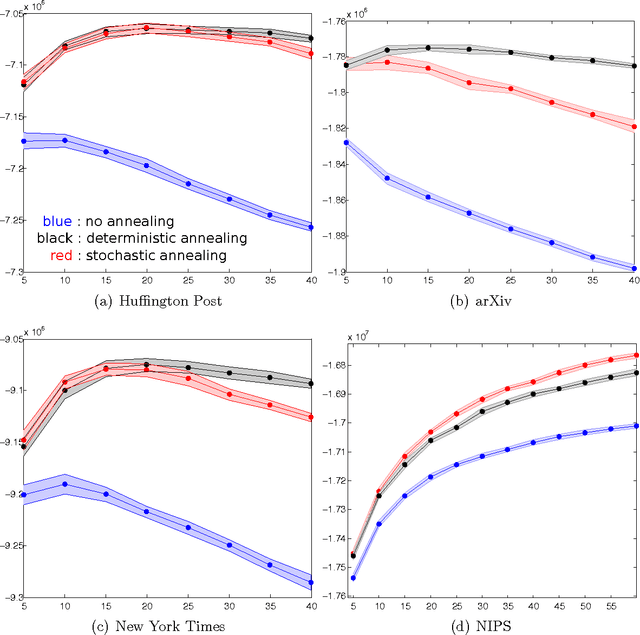
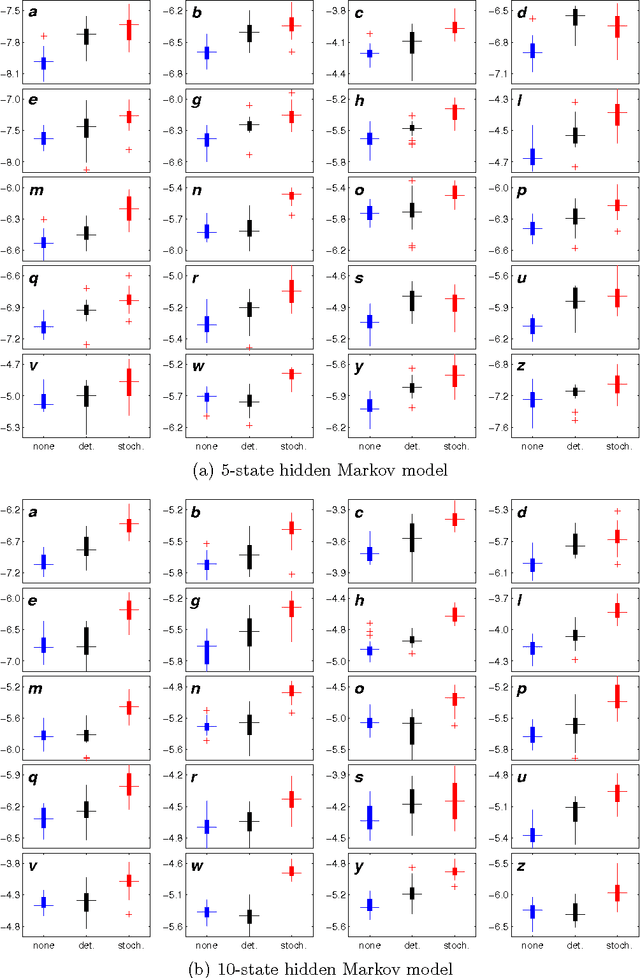
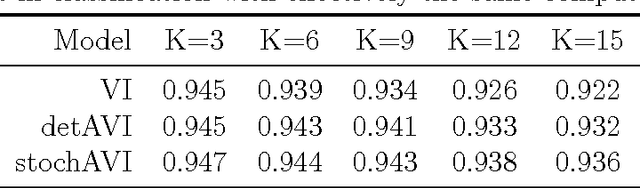
We empirically evaluate a stochastic annealing strategy for Bayesian posterior optimization with variational inference. Variational inference is a deterministic approach to approximate posterior inference in Bayesian models in which a typically non-convex objective function is locally optimized over the parameters of the approximating distribution. We investigate an annealing method for optimizing this objective with the aim of finding a better local optimal solution and compare with deterministic annealing methods and no annealing. We show that stochastic annealing can provide clear improvement on the GMM and HMM, while performance on LDA tends to favor deterministic annealing methods.

A Collaborative Kalman Filter for Time-Evolving Dyadic Processes

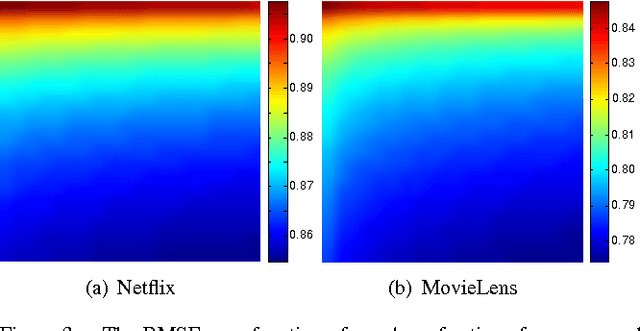
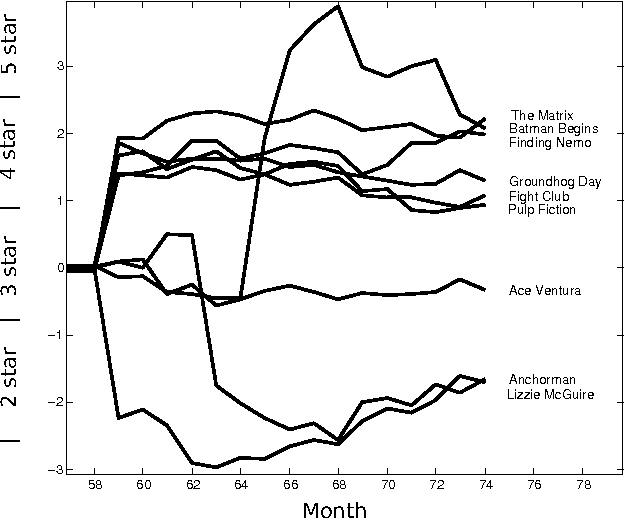
We present the collaborative Kalman filter (CKF), a dynamic model for collaborative filtering and related factorization models. Using the matrix factorization approach to collaborative filtering, the CKF accounts for time evolution by modeling each low-dimensional latent embedding as a multidimensional Brownian motion. Each observation is a random variable whose distribution is parameterized by the dot product of the relevant Brownian motions at that moment in time. This is naturally interpreted as a Kalman filter with multiple interacting state space vectors. We also present a method for learning a dynamically evolving drift parameter for each location by modeling it as a geometric Brownian motion. We handle posterior intractability via a mean-field variational approximation, which also preserves tractability for downstream calculations in a manner similar to the Kalman filter. We evaluate the model on several large datasets, providing quantitative evaluation on the 10 million Movielens and 100 million Netflix datasets and qualitative evaluation on a set of 39 million stock returns divided across roughly 6,500 companies from the years 1962-2014.

Bayesian Nonparametric Dictionary Learning for Compressed Sensing MRI

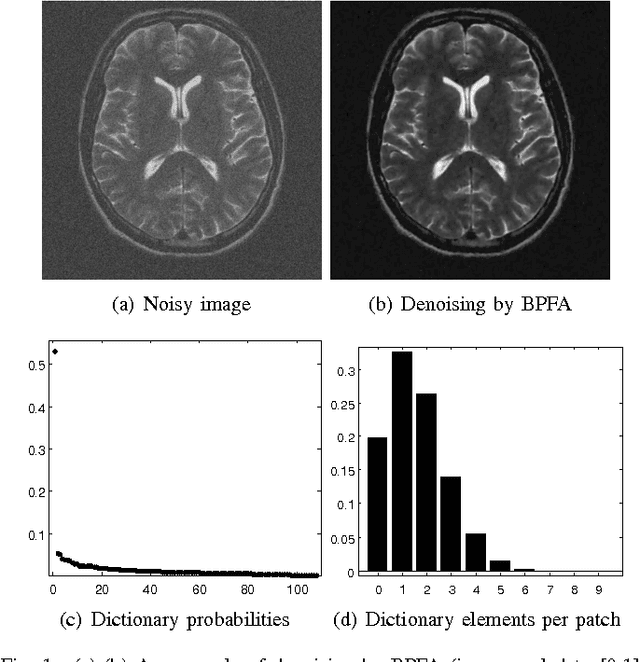
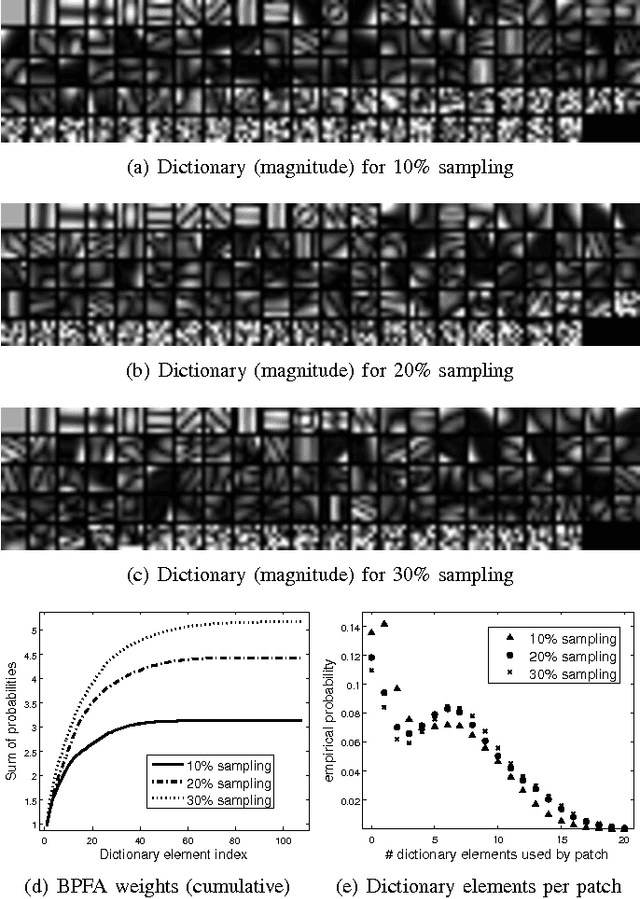
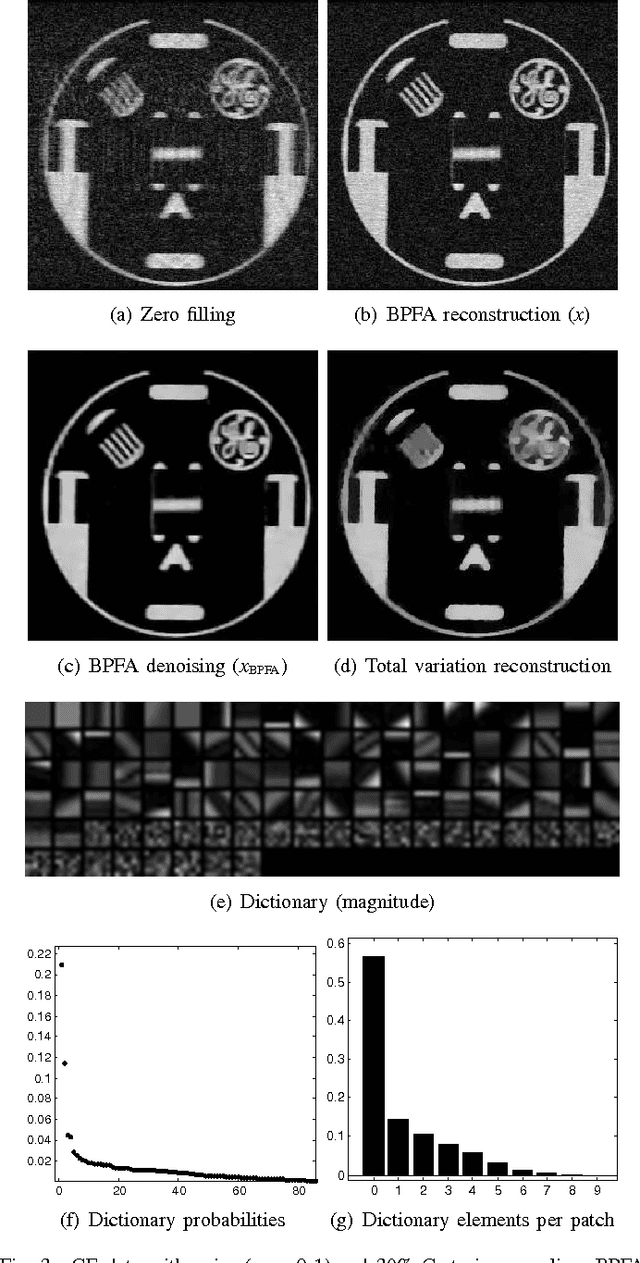
We develop a Bayesian nonparametric model for reconstructing magnetic resonance images (MRI) from highly undersampled k-space data. We perform dictionary learning as part of the image reconstruction process. To this end, we use the beta process as a nonparametric dictionary learning prior for representing an image patch as a sparse combination of dictionary elements. The size of the dictionary and the patch-specific sparsity pattern are inferred from the data, in addition to other dictionary learning variables. Dictionary learning is performed directly on the compressed image, and so is tailored to the MRI being considered. In addition, we investigate a total variation penalty term in combination with the dictionary learning model, and show how the denoising property of dictionary learning removes dependence on regularization parameters in the noisy setting. We derive a stochastic optimization algorithm based on Markov Chain Monte Carlo (MCMC) for the Bayesian model, and use the alternating direction method of multipliers (ADMM) for efficiently performing total variation minimization. We present empirical results on several MRI, which show that the proposed regularization framework can improve reconstruction accuracy over other methods.

Nested Hierarchical Dirichlet Processes

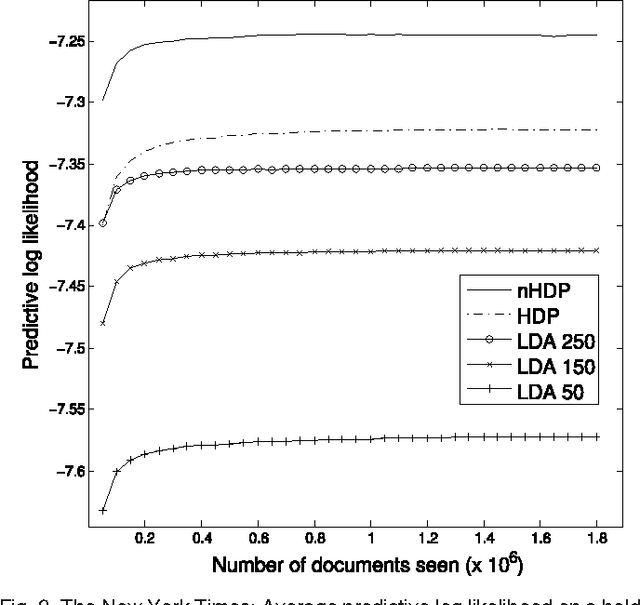
We develop a nested hierarchical Dirichlet process (nHDP) for hierarchical topic modeling. The nHDP is a generalization of the nested Chinese restaurant process (nCRP) that allows each word to follow its own path to a topic node according to a document-specific distribution on a shared tree. This alleviates the rigid, single-path formulation of the nCRP, allowing a document to more easily express thematic borrowings as a random effect. We derive a stochastic variational inference algorithm for the model, in addition to a greedy subtree selection method for each document, which allows for efficient inference using massive collections of text documents. We demonstrate our algorithm on 1.8 million documents from The New York Times and 3.3 million documents from Wikipedia.

Combinatorial clustering and the beta negative binomial process

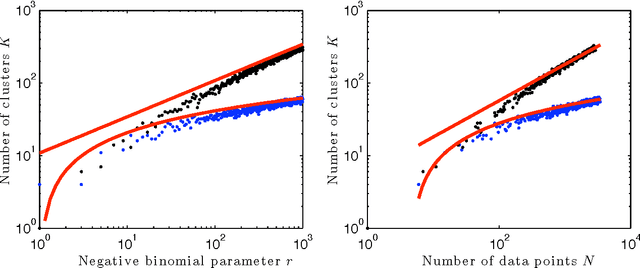
We develop a Bayesian nonparametric approach to a general family of latent class problems in which individuals can belong simultaneously to multiple classes and where each class can be exhibited multiple times by an individual. We introduce a combinatorial stochastic process known as the negative binomial process (NBP) as an infinite-dimensional prior appropriate for such problems. We show that the NBP is conjugate to the beta process, and we characterize the posterior distribution under the beta-negative binomial process (BNBP) and hierarchical models based on the BNBP (the HBNBP). We study the asymptotic properties of the BNBP and develop a three-parameter extension of the BNBP that exhibits power-law behavior. We derive MCMC algorithms for posterior inference under the HBNBP, and we present experiments using these algorithms in the domains of image segmentation, object recognition, and document analysis.