Optimal Energy Shaping Control for a Backdrivable Hip Exoskeleton

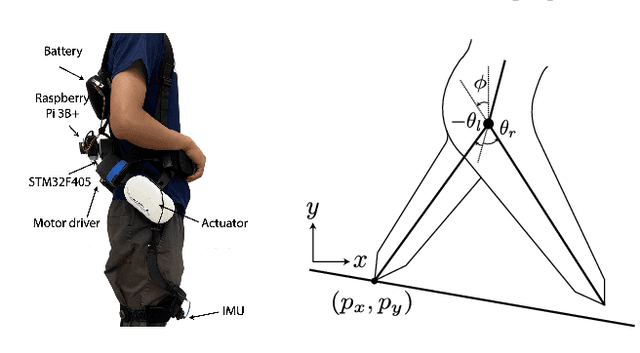
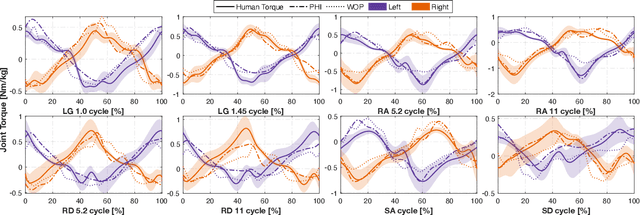
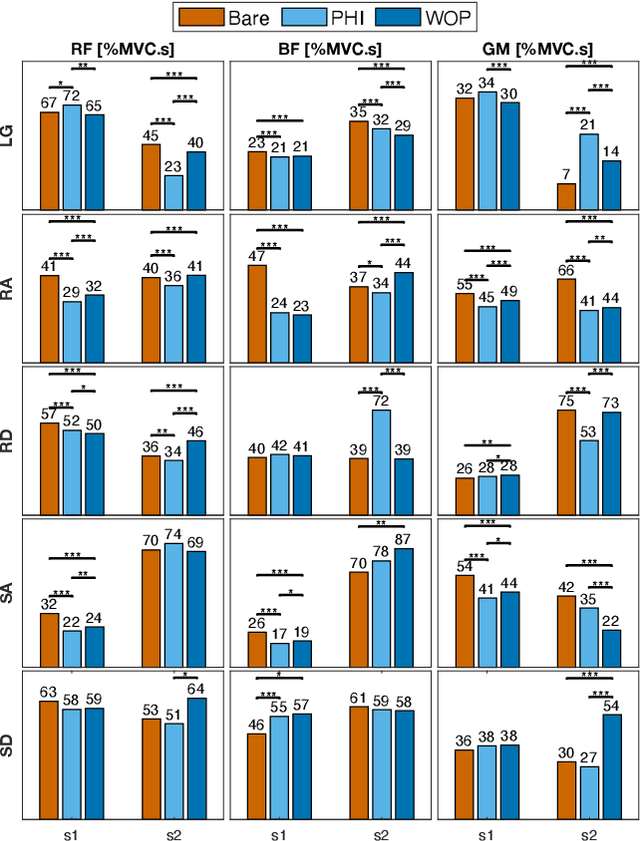
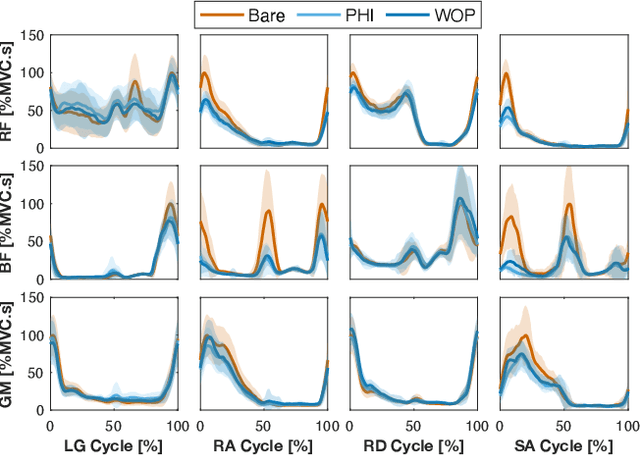
Task-dependent controllers widely used in exoskeletons track predefined trajectories, which overly constrain the volitional motion of individuals with remnant voluntary mobility. Energy shaping, on the other hand, provides task-invariant assistance by altering the human body's dynamic characteristics in the closed loop. While human-exoskeleton systems are often modeled using Euler-Lagrange equations, in our previous work we modeled the system as a port-controlled-Hamiltonian system, and a task-invariant controller was designed for a knee-ankle exoskeleton using interconnection-damping assignment passivity-based control. In this paper, we extend this framework to design a controller for a backdrivable hip exoskeleton to assist multiple tasks. A set of basis functions that contains information of kinematics is selected and corresponding coefficients are optimized, which allows the controller to provide torque that fits normative human torque for different activities of daily life. Human-subject experiments with two able-bodied subjects demonstrated the controller's capability to reduce muscle effort across different tasks.

Learning the mapping $\mathbf{x}\mapsto \sum_{i=1}^d x_i^2$: the cost of finding the needle in a haystack

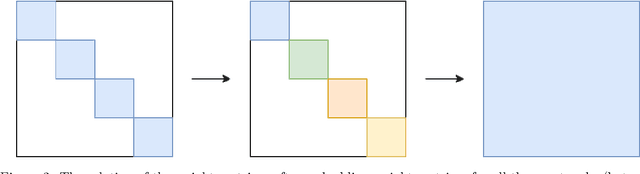
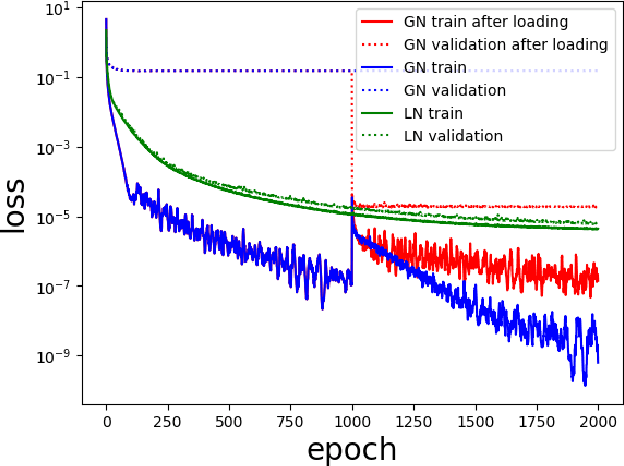
The task of using machine learning to approximate the mapping $\mathbf{x}\mapsto\sum_{i=1}^d x_i^2$ with $x_i\in[-1,1]$ seems to be a trivial one. Given the knowledge of the separable structure of the function, one can design a sparse network to represent the function very accurately, or even exactly. When such structural information is not available, and we may only use a dense neural network, the optimization procedure to find the sparse network embedded in the dense network is similar to finding the needle in a haystack, using a given number of samples of the function. We demonstrate that the cost (measured by sample complexity) of finding the needle is directly related to the Barron norm of the function. While only a small number of samples is needed to train a sparse network, the dense network trained with the same number of samples exhibits large test loss and a large generalization gap. In order to control the size of the generalization gap, we find that the use of explicit regularization becomes increasingly more important as $d$ increases. The numerically observed sample complexity with explicit regularization scales as $\mathcal{O}(d^{2.5})$, which is in fact better than the theoretically predicted sample complexity that scales as $\mathcal{O}(d^{4})$. Without explicit regularization (also called implicit regularization), the numerically observed sample complexity is significantly higher and is close to $\mathcal{O}(d^{4.5})$.

Deep Density: circumventing the Kohn-Sham equations via symmetry preserving neural networks

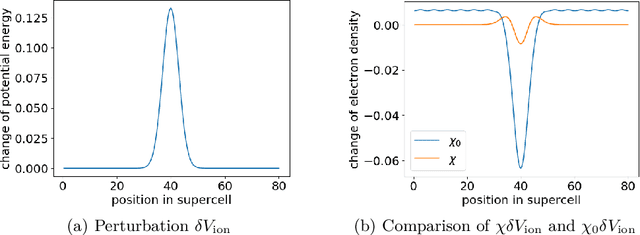
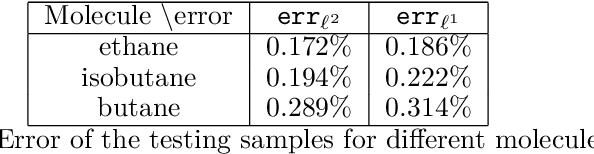
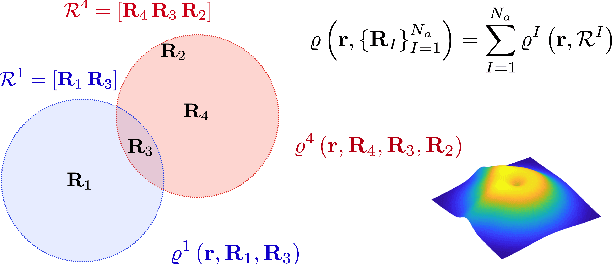
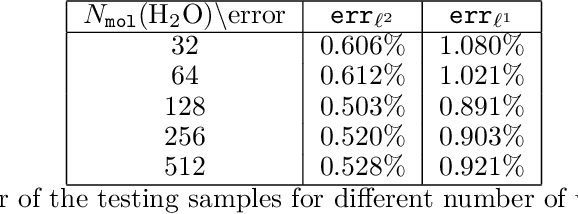
The recently developed Deep Potential [Phys. Rev. Lett. 120, 143001, 2018] is a powerful method to represent general inter-atomic potentials using deep neural networks. The success of Deep Potential rests on the proper treatment of locality and symmetry properties of each component of the network. In this paper, we leverage its network structure to effectively represent the mapping from the atomic configuration to the electron density in Kohn-Sham density function theory (KS-DFT). By directly targeting at the self-consistent electron density, we demonstrate that the adapted network architecture, called the Deep Density, can effectively represent the electron density as the linear combination of contributions from many local clusters. The network is constructed to satisfy the translation, rotation, and permutation symmetries, and is designed to be transferable to different system sizes. We demonstrate that using a relatively small number of training snapshots, Deep Density achieves excellent performance for one-dimensional insulating and metallic systems, as well as systems with mixed insulating and metallic characters. We also demonstrate its performance for real three-dimensional systems, including small organic molecules, as well as extended systems such as water (up to $512$ molecules) and aluminum (up to $256$ atoms).