Learning the mapping $\mathbf{x}\mapsto \sum_{i=1}^d x_i^2$: the cost of finding the needle in a haystack
Paper and Code
Feb 24, 2020
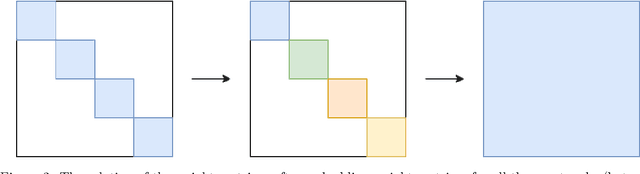

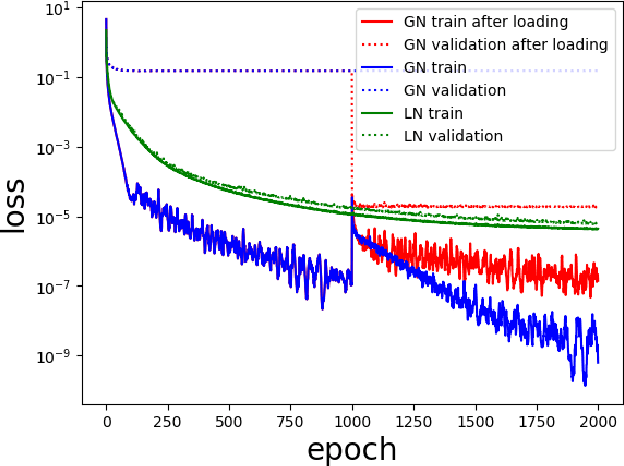
The task of using machine learning to approximate the mapping $\mathbf{x}\mapsto\sum_{i=1}^d x_i^2$ with $x_i\in[-1,1]$ seems to be a trivial one. Given the knowledge of the separable structure of the function, one can design a sparse network to represent the function very accurately, or even exactly. When such structural information is not available, and we may only use a dense neural network, the optimization procedure to find the sparse network embedded in the dense network is similar to finding the needle in a haystack, using a given number of samples of the function. We demonstrate that the cost (measured by sample complexity) of finding the needle is directly related to the Barron norm of the function. While only a small number of samples is needed to train a sparse network, the dense network trained with the same number of samples exhibits large test loss and a large generalization gap. In order to control the size of the generalization gap, we find that the use of explicit regularization becomes increasingly more important as $d$ increases. The numerically observed sample complexity with explicit regularization scales as $\mathcal{O}(d^{2.5})$, which is in fact better than the theoretically predicted sample complexity that scales as $\mathcal{O}(d^{4})$. Without explicit regularization (also called implicit regularization), the numerically observed sample complexity is significantly higher and is close to $\mathcal{O}(d^{4.5})$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge