Sparse Equation Matching: A Derivative-Free Learning for General-Order Dynamical Systems

Equation discovery is a fundamental learning task for uncovering the underlying dynamics of complex systems, with wide-ranging applications in areas such as brain connectivity analysis, climate modeling, gene regulation, and physical system simulation. However, many existing approaches rely on accurate derivative estimation and are limited to first-order dynamical systems, restricting their applicability to real-world scenarios. In this work, we propose sparse equation matching (SEM), a unified framework that encompasses several existing equation discovery methods under a common formulation. SEM introduces an integral-based sparse regression method using Green's functions, enabling derivative-free estimation of differential operators and their associated driving functions in general-order dynamical systems. The effectiveness of SEM is demonstrated through extensive simulations, benchmarking its performance against derivative-based approaches. We then apply SEM to electroencephalographic (EEG) data recorded during multiple oculomotor tasks, collected from 52 participants in a brain-computer interface experiment. Our method identifies active brain regions across participants and reveals task-specific connectivity patterns. These findings offer valuable insights into brain connectivity and the underlying neural mechanisms.

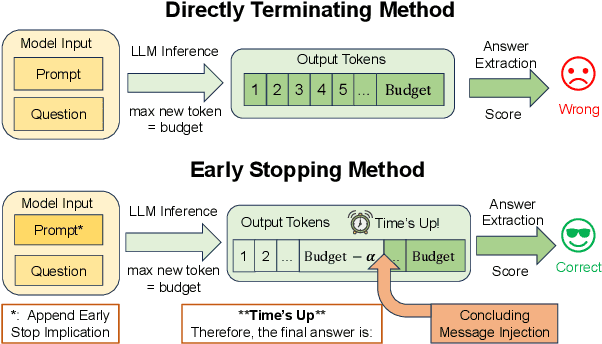
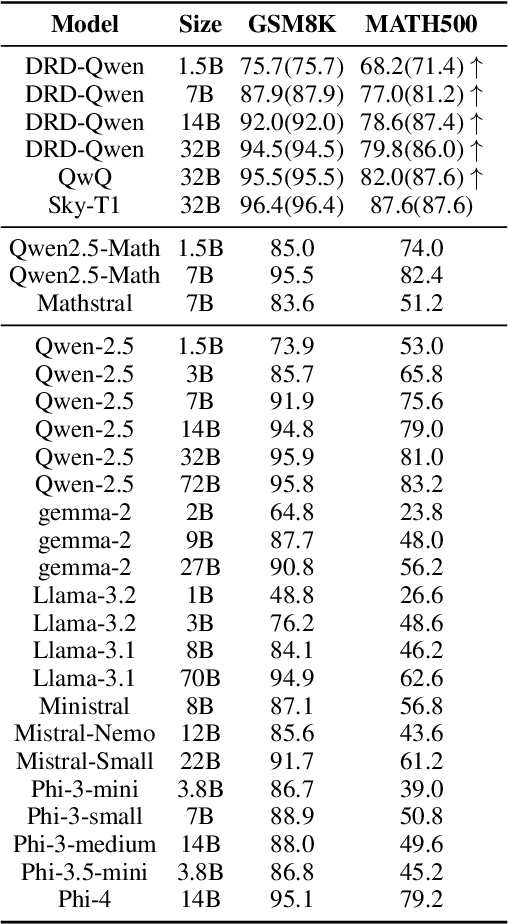
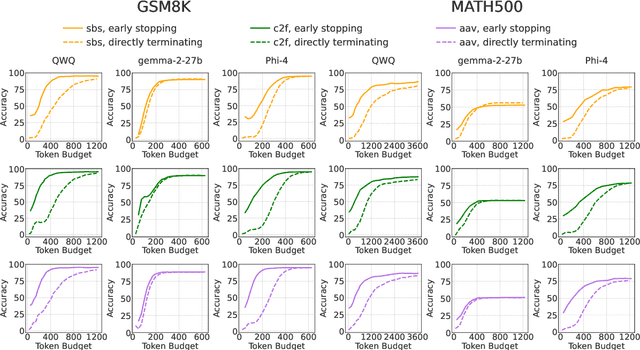
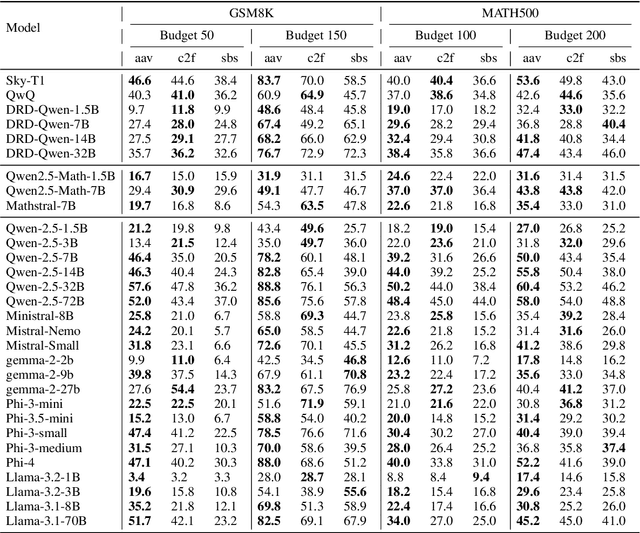
Time's Up! An Empirical Study of LLM Reasoning Ability Under Output Length Constraint

Recent work has demonstrated the remarkable potential of Large Language Models (LLMs) in test-time scaling. By making the models think before answering, they are able to achieve much higher accuracy with extra inference computation. However, in many real-world scenarios, models are used under time constraints, where an answer should be given to the user within a certain output length. It is unclear whether and how the reasoning abilities of LLMs remain effective under such constraints. We take a first look at this problem by conducting an in-depth empirical study. Specifically, we test more than 25 LLMs on common reasoning datasets under a wide range of output length budgets, and we analyze the correlation between the inference accuracy and various properties including model type, model size, prompt style, etc. We also consider the mappings between the token budgets and the actual on-device latency budgets. The results have demonstrated several interesting findings regarding the budget-aware LLM reasoning that differ from the unconstrained situation, e.g. the optimal choices of model sizes and prompts change under different budgets. These findings offer practical guidance for users to deploy LLMs under real-world latency constraints.