Score-based 3D molecule generation with neural fields

We introduce a new representation for 3D molecules based on their continuous atomic density fields. Using this representation, we propose a new model based on walk-jump sampling for unconditional 3D molecule generation in the continuous space using neural fields. Our model, FuncMol, encodes molecular fields into latent codes using a conditional neural field, samples noisy codes from a Gaussian-smoothed distribution with Langevin MCMC (walk), denoises these samples in a single step (jump), and finally decodes them into molecular fields. FuncMol performs all-atom generation of 3D molecules without assumptions on the molecular structure and scales well with the size of molecules, unlike most approaches. Our method achieves competitive results on drug-like molecules and easily scales to macro-cyclic peptides, with at least one order of magnitude faster sampling. The code is available at https://github.com/prescient-design/funcmol.

JAMUN: Transferable Molecular Conformational Ensemble Generation with Walk-Jump Sampling

Conformational ensembles of protein structures are immensely important both to understanding protein function, and for drug discovery in novel modalities such as cryptic pockets. Current techniques for sampling ensembles are computationally inefficient, or do not transfer to systems outside their training data. We present walk-Jump Accelerated Molecular ensembles with Universal Noise (JAMUN), a step towards the goal of efficiently sampling the Boltzmann distribution of arbitrary proteins. By extending Walk-Jump Sampling to point clouds, JAMUN enables ensemble generation at orders of magnitude faster rates than traditional molecular dynamics or state-of-the-art ML methods. Further, JAMUN is able to predict the stable basins of small peptides that were not seen during training.

NEBULA: Neural Empirical Bayes Under Latent Representations for Efficient and Controllable Design of Molecular Libraries

We present NEBULA, the first latent 3D generative model for scalable generation of large molecular libraries around a seed compound of interest. Such libraries are crucial for scientific discovery, but it remains challenging to generate large numbers of high quality samples efficiently. 3D-voxel-based methods have recently shown great promise for generating high quality samples de novo from random noise (Pinheiro et al., 2023). However, sampling in 3D-voxel space is computationally expensive and use in library generation is prohibitively slow. Here, we instead perform neural empirical Bayes sampling (Saremi & Hyvarinen, 2019) in the learned latent space of a vector-quantized variational autoencoder. NEBULA generates large molecular libraries nearly an order of magnitude faster than existing methods without sacrificing sample quality. Moreover, NEBULA generalizes better to unseen drug-like molecules, as demonstrated on two public datasets and multiple recently released drugs. We expect the approach herein to be highly enabling for machine learning-based drug discovery. The code is available at https://github.com/prescient-design/nebula

Structure-based drug design by denoising voxel grids

We present VoxBind, a new score-based generative model for 3D molecules conditioned on protein structures. Our approach represents molecules as 3D atomic density grids and leverages a 3D voxel-denoising network for learning and generation. We extend the neural empirical Bayes formalism (Saremi & Hyvarinen, 2019) to the conditional setting and generate structure-conditioned molecules with a two-step procedure: (i) sample noisy molecules from the Gaussian-smoothed conditional distribution with underdamped Langevin MCMC using the learned score function and (ii) estimate clean molecules from the noisy samples with single-step denoising. Compared to the current state of the art, our model is simpler to train, significantly faster to sample from, and achieves better results on extensive in silico benchmarks -- the generated molecules are more diverse, exhibit fewer steric clashes, and bind with higher affinity to protein pockets.

3D molecule generation by denoising voxel grids

We propose a new score-based approach to generate 3D molecules represented as atomic densities on regular grids. First, we train a denoising neural network that learns to map from a smooth distribution of noisy molecules to the distribution of real molecules. Then, we follow the neural empirical Bayes framework [Saremi and Hyvarinen, 2019] and generate molecules in two steps: (i) sample noisy density grids from a smooth distribution via underdamped Langevin Markov chain Monte Carlo, and (ii) recover the ``clean'' molecule by denoising the noisy grid with a single step. Our method, VoxMol, generates molecules in a fundamentally different way than the current state of the art (i.e., diffusion models applied to atom point clouds). It differs in terms of the data representation, the noise model, the network architecture and the generative modeling algorithm. VoxMol achieves comparable results to state of the art on unconditional 3D molecule generation while being simpler to train and faster to generate molecules.

Protein Discovery with Discrete Walk-Jump Sampling

We resolve difficulties in training and sampling from a discrete generative model by learning a smoothed energy function, sampling from the smoothed data manifold with Langevin Markov chain Monte Carlo (MCMC), and projecting back to the true data manifold with one-step denoising. Our Discrete Walk-Jump Sampling formalism combines the maximum likelihood training of an energy-based model and improved sample quality of a score-based model, while simplifying training and sampling by requiring only a single noise level. We evaluate the robustness of our approach on generative modeling of antibody proteins and introduce the distributional conformity score to benchmark protein generative models. By optimizing and sampling from our models for the proposed distributional conformity score, 97-100% of generated samples are successfully expressed and purified and 35% of functional designs show equal or improved binding affinity compared to known functional antibodies on the first attempt in a single round of laboratory experiments. We also report the first demonstration of long-run fast-mixing MCMC chains where diverse antibody protein classes are visited in a single MCMC chain.

Chain of Log-Concave Markov Chains

Markov chain Monte Carlo (MCMC) is a class of general-purpose algorithms for sampling from unnormalized densities. There are two well-known problems facing MCMC in high dimensions: (i) The distributions of interest are concentrated in pockets separated by large regions with small probability mass, and (ii) The log-concave pockets themselves are typically ill-conditioned. We introduce a framework to tackle these problems using isotropic Gaussian smoothing. We prove one can always decompose sampling from a density (minimal assumptions made on the density) into a sequence of sampling from log-concave conditional densities via accumulation of noisy measurements with equal noise levels. This construction keeps track of a history of samples, making it non-Markovian as a whole, but the history only shows up in the form of an empirical mean, making the memory footprint minimal. Our sampling algorithm generalizes walk-jump sampling [1]. The "walk" phase becomes a (non-Markovian) chain of log-concave Langevin chains. The "jump" from the accumulated measurements is obtained by empirical Bayes. We study our sampling algorithm quantitatively using the 2-Wasserstein metric and compare it with various Langevin MCMC algorithms. We also report a remarkable capacity of our algorithm to "tunnel" between modes of a distribution.

Universal Smoothed Score Functions for Generative Modeling

We consider the problem of generative modeling based on smoothing an unknown density of interest in $\mathbb{R}^d$ using factorial kernels with $M$ independent Gaussian channels with equal noise levels introduced by Saremi and Srivastava (2022). First, we fully characterize the time complexity of learning the resulting smoothed density in $\mathbb{R}^{Md}$, called M-density, by deriving a universal form for its parametrization in which the score function is by construction permutation equivariant. Next, we study the time complexity of sampling an M-density by analyzing its condition number for Gaussian distributions. This spectral analysis gives a geometric insight on the "shape" of M-densities as one increases $M$. Finally, we present results on the sample quality in this class of generative models on the CIFAR-10 dataset where we report Fr\'echet inception distances (14.15), notably obtained with a single noise level on long-run fast-mixing MCMC chains.

PropertyDAG: Multi-objective Bayesian optimization of partially ordered, mixed-variable properties for biological sequence design

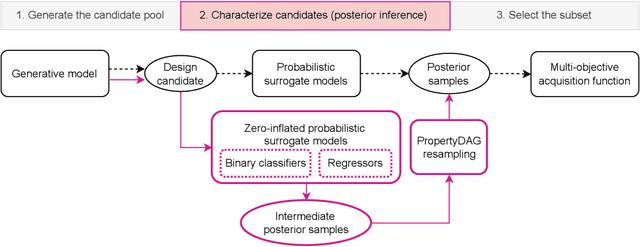
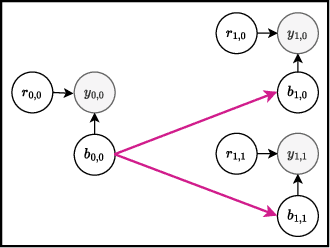
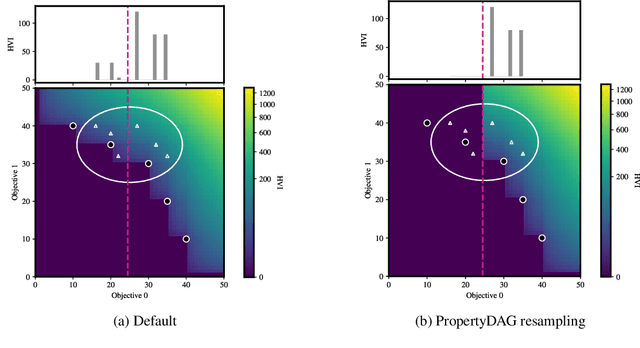
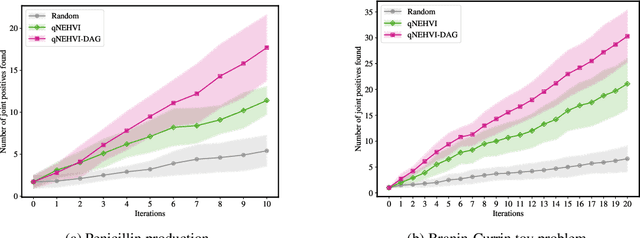
Bayesian optimization offers a sample-efficient framework for navigating the exploration-exploitation trade-off in the vast design space of biological sequences. Whereas it is possible to optimize the various properties of interest jointly using a multi-objective acquisition function, such as the expected hypervolume improvement (EHVI), this approach does not account for objectives with a hierarchical dependency structure. We consider a common use case where some regions of the Pareto frontier are prioritized over others according to a specified $\textit{partial ordering}$ in the objectives. For instance, when designing antibodies, we would like to maximize the binding affinity to a target antigen only if it can be expressed in live cell culture -- modeling the experimental dependency in which affinity can only be measured for antibodies that can be expressed and thus produced in viable quantities. In general, we may want to confer a partial ordering to the properties such that each property is optimized conditioned on its parent properties satisfying some feasibility condition. To this end, we present PropertyDAG, a framework that operates on top of the traditional multi-objective BO to impose this desired ordering on the objectives, e.g. expression $\rightarrow$ affinity. We demonstrate its performance over multiple simulated active learning iterations on a penicillin production task, toy numerical problem, and a real-world antibody design task.

Multimeasurement Generative Models

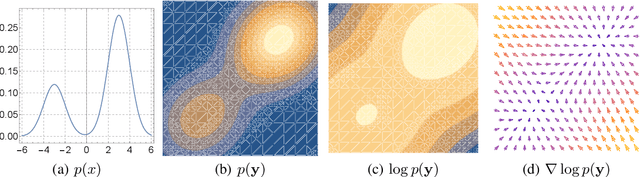
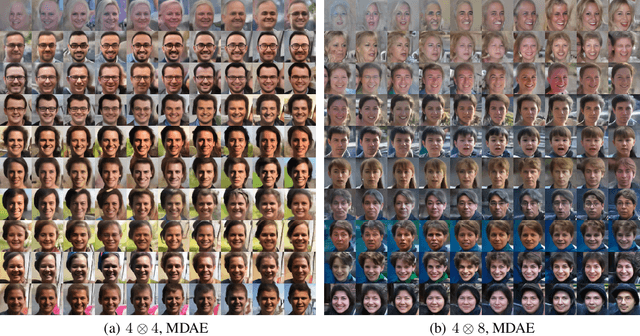
We formally map the problem of sampling from an unknown distribution with density $p_X$ in $\mathbb{R}^d$ to the problem of learning and sampling $p_\mathbf{Y}$ in $\mathbb{R}^{Md}$ obtained by convolving $p_X$ with a fixed factorial kernel: $p_\mathbf{Y}$ is referred to as M-density and the factorial kernel as multimeasurement noise model (MNM). The M-density is smoother than $p_X$, easier to learn and sample from, yet for large $M$ the two problems are mathematically equivalent since $X$ can be estimated exactly given $\mathbf{Y}=\mathbf{y}$ using the Bayes estimator $\widehat{x}(\mathbf{y})=\mathbb{E}[X\vert\mathbf{Y}=\mathbf{y}]$. To formulate the problem, we derive $\widehat{x}(\mathbf{y})$ for Poisson and Gaussian MNMs expressed in closed form in terms of unnormalized $p_\mathbf{Y}$. This leads to a simple least-squares objective for learning parametric energy and score functions. We present various parametrization schemes of interest, including one in which studying Gaussian M-densities directly leads to multidenoising autoencoders--this is the first theoretical connection made between denoising autoencoders and empirical Bayes in the literature. Samples from $p_X$ are obtained by walk-jump sampling (Saremi & Hyvarinen, 2019) via underdamped Langevin MCMC (walk) to sample from $p_\mathbf{Y}$ and the multimeasurement Bayes estimation of $X$ (jump). We study permutation invariant Gaussian M-densities on MNIST, CIFAR-10, and FFHQ-256 datasets, and demonstrate the effectiveness of this framework for realizing fast-mixing stable Markov chains in high dimensions.