Decentralized Adaptive Control for Collaborative Manipulation of Rigid Bodies

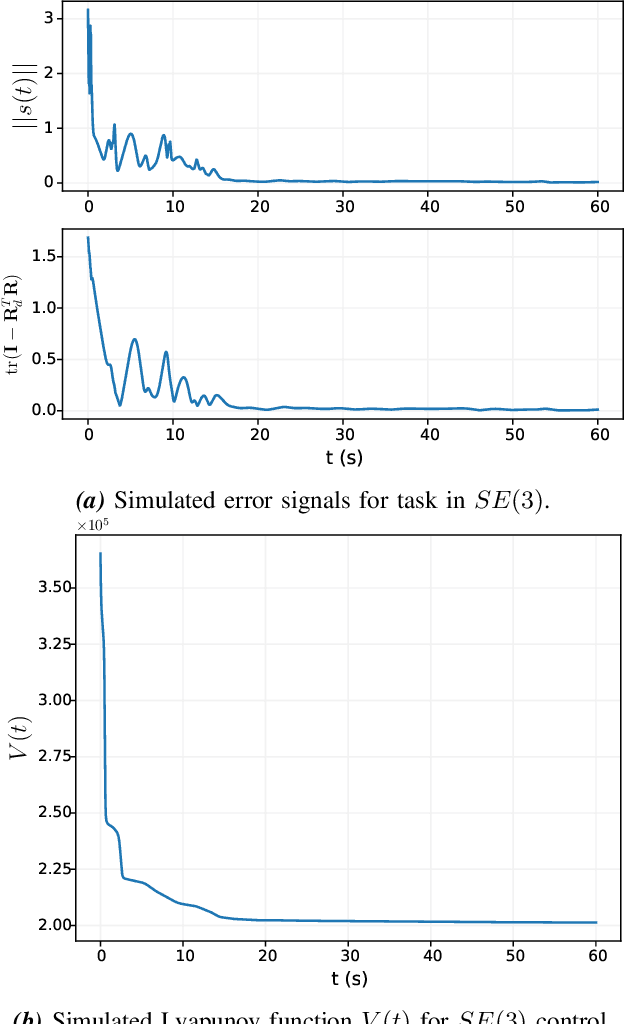
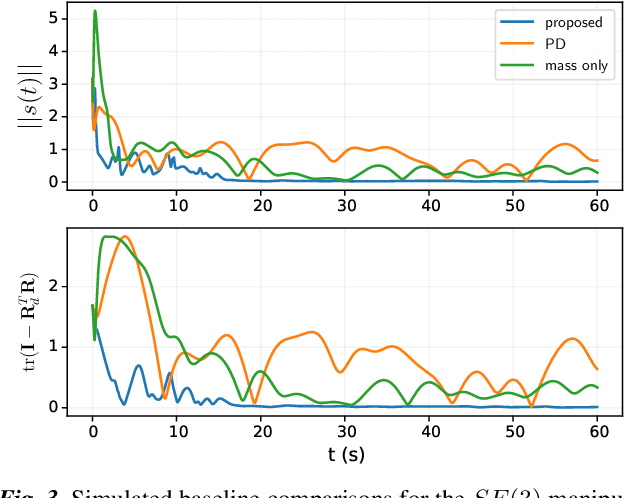
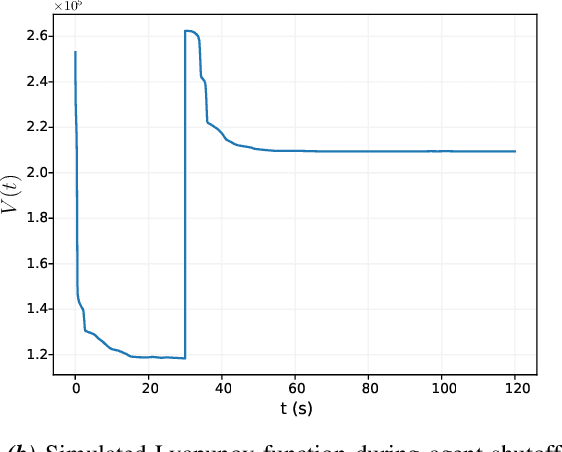
In this work, we consider a group of robots working together to manipulate a rigid object to track a desired trajectory in $SE(3)$. The robots have no explicit communication network among them, and they do no know the mass or friction properties of the object, or where they are attached to the object. However, we assume they share data from a common IMU placed arbitrarily on the object. To solve this problem, we propose a decentralized adaptive control scheme wherein each agent maintains and adapts its own estimate of the object parameters in order to track a reference trajectory. We present an analysis of the controller's behavior, and show that all closed-loop signals remain bounded, and that the system trajectory will almost always (except for initial conditions on a set of measure zero) converge to the desired trajectory. We study the proposed controller's performance using numerical simulations of a manipulation task in 3D, and with hardware experiments which demonstrate our algorithm on a planar manipulation task. These studies, taken together, demonstrate the effectiveness of the proposed controller even in the presence of numerous unmodelled effects, such as discretization errors and complex frictional interactions.

Higher-order algorithms and implicit regularization for nonlinearly parameterized adaptive control

Stable concurrent learning and control of dynamical systems is the subject of adaptive control. Adaptive control is a field with many practical applications and a rich theory, but much of the development for nonlinear systems revolves around a few key algorithms. By exploiting strong connections between nonlinear adaptive control techniques and recent progress in optimization and machine learning, we show that there exists considerable untapped potential in algorithm development for nonlinear adaptive control. We present a large set of new globally convergent adaptive control algorithms that are applicable both to linearly parameterized systems and to nonlinearly parameterized systems satisfying a certain monotonicity requirement. We adopt a variational formalism based on the Bregman Lagrangian to define a general framework that systematically generates higher-order in-time velocity gradient algorithms. We generalize our algorithms to the non-Euclidean setting and show that the Euler Lagrange equations for the Bregman Lagrangian lead to natural gradient and mirror descent-like adaptation laws with momentum that incorporate local geometry through a Hessian metric specified by a convex function. We prove that these non-Euclidean adaptation laws implicitly regularize the system model by minimizing the convex function that specifies the metric throughout adaptation. Local geometry imposed during adaptation thus may be used to select parameter vectors - out of the many that will lead to perfect tracking - for desired properties such as sparsity. We illustrate our analysis with simulations using a higher-order algorithm for nonlinearly parameterized systems to learn regularized hidden layer weights in a three-layer feedforward neural network.

Learning Stabilizable Nonlinear Dynamics with Contraction-Based Regularization

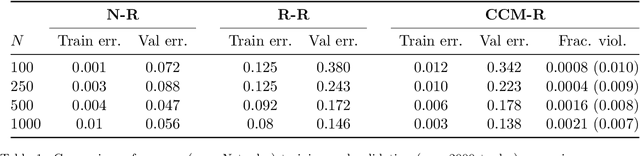
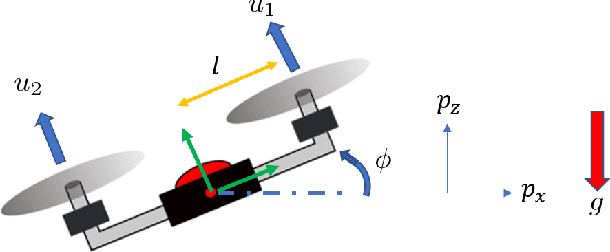
We propose a novel framework for learning stabilizable nonlinear dynamical systems for continuous control tasks in robotics. The key contribution is a control-theoretic regularizer for dynamics fitting rooted in the notion of stabilizability, a constraint which guarantees the existence of robust tracking controllers for arbitrary open-loop trajectories generated with the learned system. Leveraging tools from contraction theory and statistical learning in Reproducing Kernel Hilbert Spaces, we formulate stabilizable dynamics learning as a functional optimization with convex objective and bi-convex functional constraints. Under a mild structural assumption and relaxation of the functional constraints to sampling-based constraints, we derive the optimal solution with a modified Representer theorem. Finally, we utilize random matrix feature approximations to reduce the dimensionality of the search parameters and formulate an iterative convex optimization algorithm that jointly fits the dynamics functions and searches for a certificate of stabilizability. We validate the proposed algorithm in simulation for a planar quadrotor, and on a quadrotor hardware testbed emulating planar dynamics. We verify, both in simulation and on hardware, significantly improved trajectory generation and tracking performance with the control-theoretic regularized model over models learned using traditional regression techniques, especially when learning from small supervised datasets. The results support the conjecture that the use of stabilizability constraints as a form of regularization can help prune the hypothesis space in a manner that is tailored to the downstream task of trajectory generation and feedback control, resulting in models that are not only dramatically better conditioned, but also data efficient.

A continuous-time analysis of distributed stochastic gradient

Synchronization in distributed networks of nonlinear dynamical systems plays a critical role in improving robustness of the individual systems to independent stochastic perturbations. Through analogy with dynamical models of biological quorum sensing, where synchronization between systems is induced through interaction with a common signal, we analyze the effect of synchronization on distributed stochastic gradient algorithms. We demonstrate that synchronization can significantly reduce the magnitude of the noise felt by the individual distributed agents and by their spatial mean. This noise reduction property is connected with a reduction in smoothing of the loss function imposed by the stochastic gradient approximation. Using similar techniques, we provide a convergence analysis, and derive a bound on the expected deviation of the spatial mean of the agents from the global minimizer of a strictly convex function. By considering additional dynamics for the quorum variable, we derive an analogous bound, and obtain new convergence results for the elastic averaging SGD algorithm. We conclude with a local analysis around a minimum of a nonconvex loss function, and show that the distributed setting leads to lower expected loss values and wider minima.

Learning Stabilizable Dynamical Systems via Control Contraction Metrics

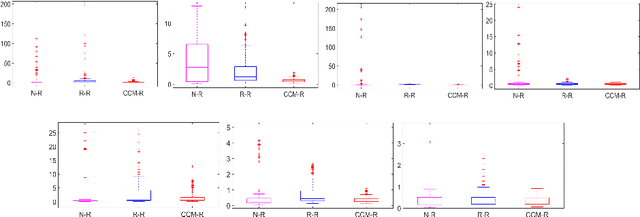
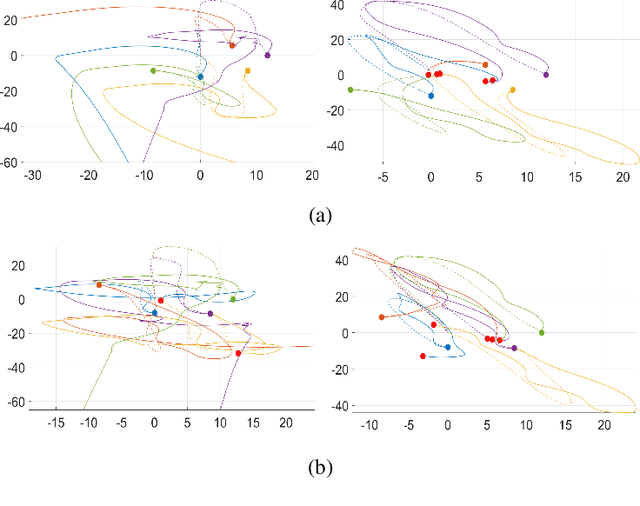
We propose a novel framework for learning stabilizable nonlinear dynamical systems for continuous control tasks in robotics. The key idea is to develop a new control-theoretic regularizer for dynamics fitting rooted in the notion of stabilizability, which guarantees that the learned system can be accompanied by a robust controller capable of stabilizing any open-loop trajectory that the system may generate. By leveraging tools from contraction theory, statistical learning, and convex optimization, we provide a general and tractable semi-supervised algorithm to learn stabilizable dynamics, which can be applied to complex underactuated systems. We validated the proposed algorithm on a simulated planar quadrotor system and observed notably improved trajectory generation and tracking performance with the control-theoretic regularized model over models learned using traditional regression techniques, especially when using a small number of demonstration examples. The results presented illustrate the need to infuse standard model-based reinforcement learning algorithms with concepts drawn from nonlinear control theory for improved reliability.

Observability in Inertial Parameter Identification

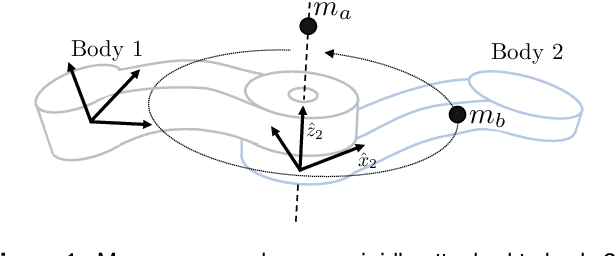
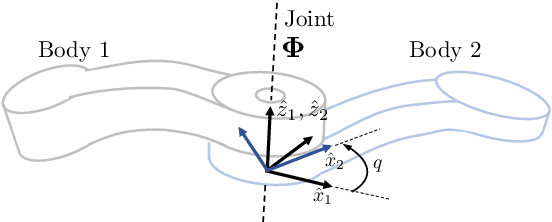
We present an algorithm to characterize the space of identifiable inertial parameters in system identification of an articulated robot. The algorithm can be applied to general open-chain kinematic trees ranging from industrial manipulators to legged robots. It is the first solution for this case that is provably correct and does not rely on symbolic techniques. The high-level operation of the algorithm is based on a key observation: Undetectable changes in inertial parameters can be interpreted as sequences of inertial transfers across the joints. Drawing on the exponential parameterization of rigid-body kinematics, undetectable inertial transfers are analyzed in terms of linear observability. This analysis can be applied recursively, and lends an overall complexity of $O(N)$ to characterize parameter identifiability for a system of N bodies. Matlab source code for the new algorithm is provided.

Cooperative Adaptive Control for Cloud-Based Robotics

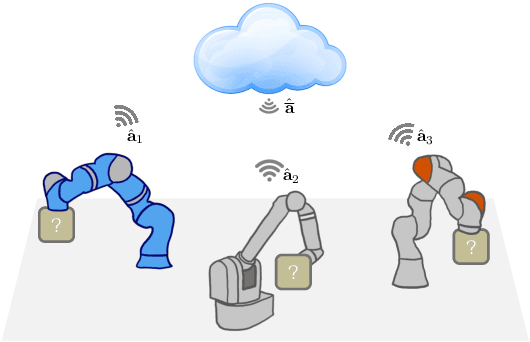
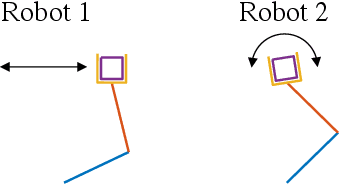
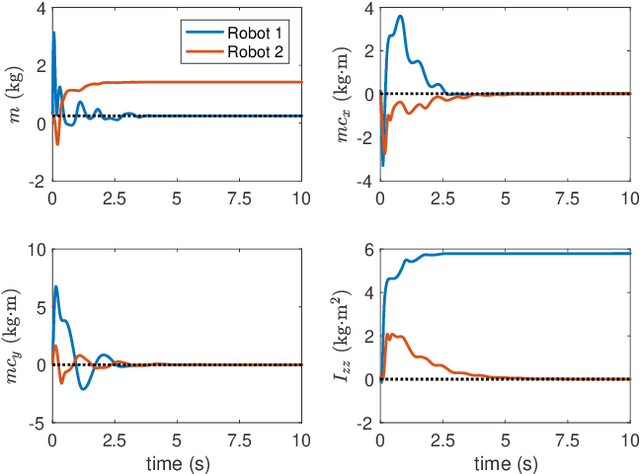
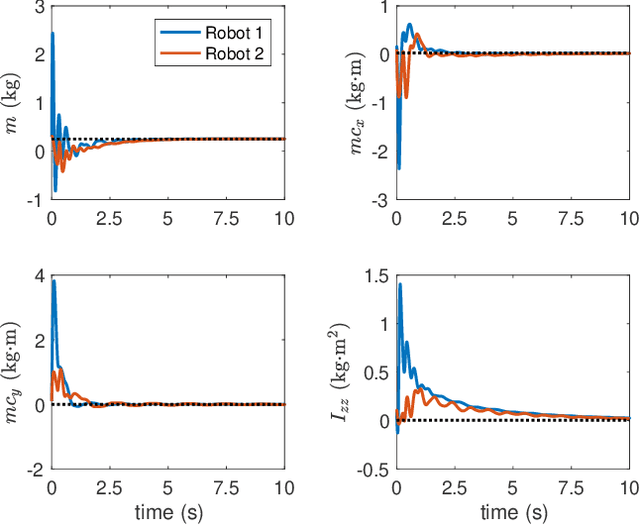
This paper studies collaboration through the cloud in the context of cooperative adaptive control for robot manipulators. We first consider the case of multiple robots manipulating a common object through synchronous centralized update laws to identify unknown inertial parameters. Through this development, we introduce a notion of Collective Sufficient Richness, wherein parameter convergence can be enabled through teamwork in the group. The introduction of this property and the analysis of stable adaptive controllers that benefit from it constitute the main new contributions of this work. Building on this original example, we then consider decentralized update laws, time-varying network topologies, and the influence of communication delays on this process. Perhaps surprisingly, these nonidealized networked conditions inherit the same benefits of convergence being determined through collective effects for the group. Simple simulations of a planar manipulator identifying an unknown load are provided to illustrate the central idea and benefits of Collective Sufficient Richness.

Control Contraction Metrics and Universal Stabilizability

In this paper we introduce the concept of universal stabilizability: the condition that every solution of a nonlinear system can be globally stabilized. We give sufficient conditions in terms of the existence of a control contraction metric, which can be found by solving a pointwise linear matrix inequality. Extensions to approximate optimal control are straightforward. The conditions we give are necessary and sufficient for linear systems and certain classes of nonlinear systems, and have interesting connections to the theory of control Lyapunov functions.

Transverse Contraction Criteria for Existence, Stability, and Robustness of a Limit Cycle

This paper derives a differential contraction condition for the existence of an orbitally-stable limit cycle in an autonomous system. This transverse contraction condition can be represented as a pointwise linear matrix inequality (LMI), thus allowing convex optimization tools such as sum-of-squares programming to be used to search for certificates of the existence of a stable limit cycle. Many desirable properties of contracting dynamics are extended to this context, including preservation of contraction under a broad class of interconnections. In addition, by introducing the concepts of differential dissipativity and transverse differential dissipativity, contraction and transverse contraction can be established for large scale systems via LMI conditions on component subsystems.