Adapting the Linearised Laplace Model Evidence for Modern Deep Learning

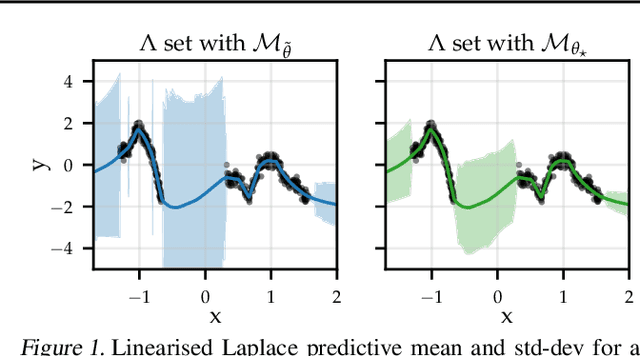
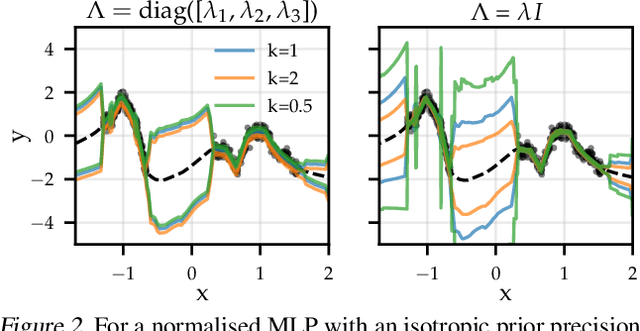
The linearised Laplace method for estimating model uncertainty has received renewed attention in the Bayesian deep learning community. The method provides reliable error bars and admits a closed-form expression for the model evidence, allowing for scalable selection of model hyperparameters. In this work, we examine the assumptions behind this method, particularly in conjunction with model selection. We show that these interact poorly with some now-standard tools of deep learning--stochastic approximation methods and normalisation layers--and make recommendations for how to better adapt this classic method to the modern setting. We provide theoretical support for our recommendations and validate them empirically on MLPs, classic CNNs, residual networks with and without normalisation layers, generative autoencoders and transformers.

A Probabilistic Deep Image Prior for Computational Tomography

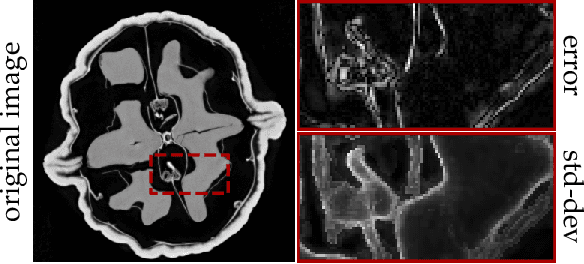
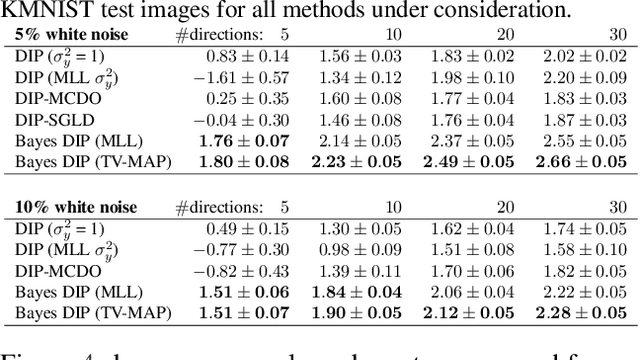
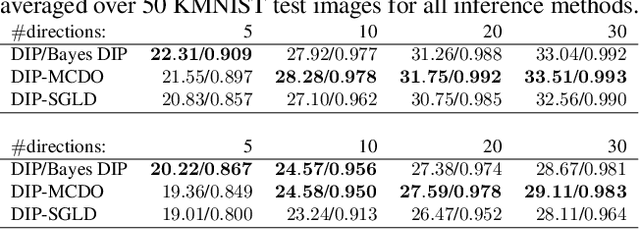
Existing deep-learning based tomographic image reconstruction methods do not provide accurate estimates of reconstruction uncertainty, hindering their real-world deployment. To address this limitation, we construct a Bayesian prior for tomographic reconstruction, which combines the classical total variation (TV) regulariser with the modern deep image prior (DIP). Specifically, we use a change of variables to connect our prior beliefs on the image TV semi-norm with the hyper-parameters of the DIP network. For the inference, we develop an approach based on the linearised Laplace method, which is scalable to high-dimensional settings. The resulting framework provides pixel-wise uncertainty estimates and a marginal likelihood objective for hyperparameter optimisation. We demonstrate the method on synthetic and real-measured high-resolution $\mu$CT data, and show that it provides superior calibration of uncertainty estimates relative to previous probabilistic formulations of the DIP.

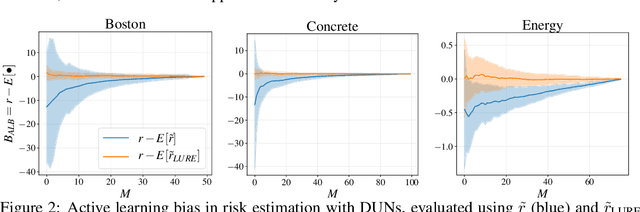
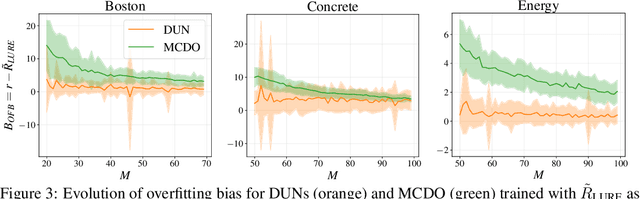
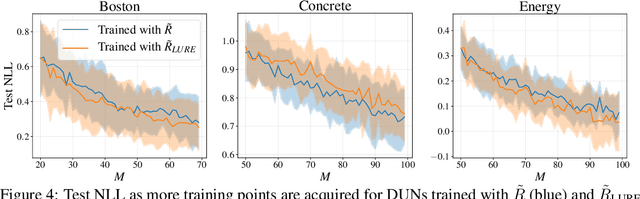
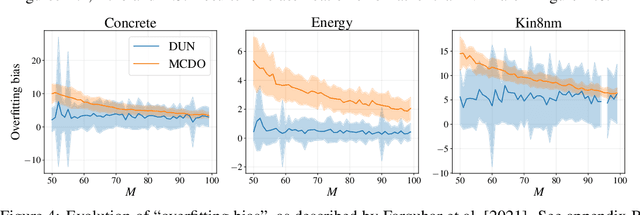
Addressing Bias in Active Learning with Depth Uncertainty Networks or Not

Farquhar et al. [2021] show that correcting for active learning bias with underparameterised models leads to improved downstream performance. For overparameterised models such as NNs, however, correction leads either to decreased or unchanged performance. They suggest that this is due to an "overfitting bias" which offsets the active learning bias. We show that depth uncertainty networks operate in a low overfitting regime, much like underparameterised models. They should therefore see an increase in performance with bias correction. Surprisingly, they do not. We propose that this negative result, as well as the results Farquhar et al. [2021], can be explained via the lens of the bias-variance decomposition of generalisation error.

Depth Uncertainty Networks for Active Learning

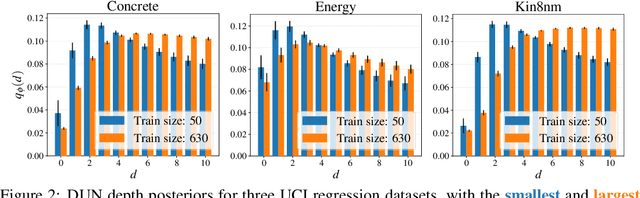
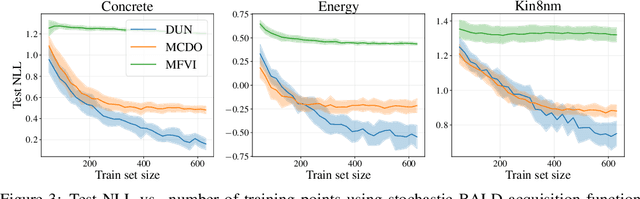
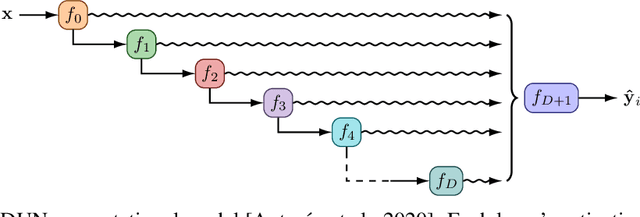
In active learning, the size and complexity of the training dataset changes over time. Simple models that are well specified by the amount of data available at the start of active learning might suffer from bias as more points are actively sampled. Flexible models that might be well suited to the full dataset can suffer from overfitting towards the start of active learning. We tackle this problem using Depth Uncertainty Networks (DUNs), a BNN variant in which the depth of the network, and thus its complexity, is inferred. We find that DUNs outperform other BNN variants on several active learning tasks. Importantly, we show that on the tasks in which DUNs perform best they present notably less overfitting than baselines.

Uncertainty as a Form of Transparency: Measuring, Communicating, and Using Uncertainty

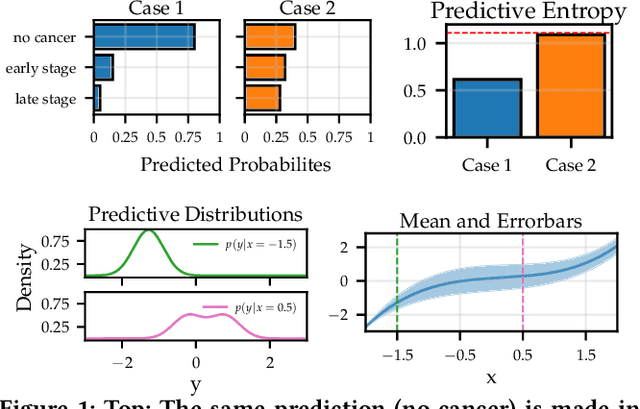
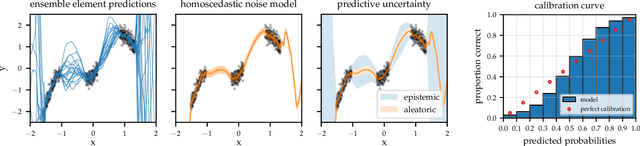
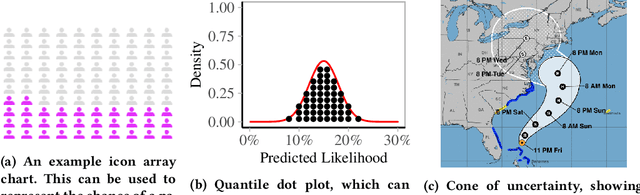
Transparency of algorithmic systems entails exposing system properties to various stakeholders for purposes that include understanding, improving, and/or contesting predictions. The machine learning (ML) community has mostly considered explainability as a proxy for transparency. With this work, we seek to encourage researchers to study uncertainty as a form of transparency and practitioners to communicate uncertainty estimates to stakeholders. First, we discuss methods for assessing uncertainty. Then, we describe the utility of uncertainty for mitigating model unfairness, augmenting decision-making, and building trustworthy systems. We also review methods for displaying uncertainty to stakeholders and discuss how to collect information required for incorporating uncertainty into existing ML pipelines. Our contribution is an interdisciplinary review to inform how to measure, communicate, and use uncertainty as a form of transparency.

Expressive yet Tractable Bayesian Deep Learning via Subnetwork Inference

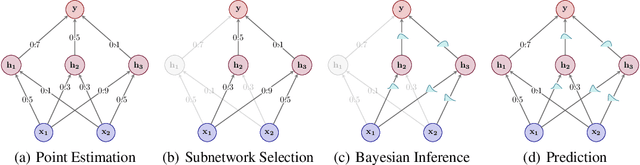
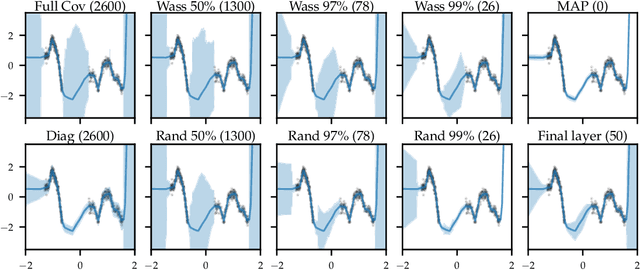
The Bayesian paradigm has the potential to solve some of the core issues in modern deep learning, such as poor calibration, data inefficiency, and catastrophic forgetting. However, scaling Bayesian inference to the high-dimensional parameter spaces of deep neural networks requires restrictive approximations. In this paper, we propose performing inference over only a small subset of the model parameters while keeping all others as point estimates. This enables us to use expressive posterior approximations that would otherwise be intractable for the full model. In particular, we develop a practical and scalable Bayesian deep learning method that first trains a point estimate, and then infers a full covariance Gaussian posterior approximation over a subnetwork. We propose a subnetwork selection procedure which aims to optimally preserve posterior uncertainty. We empirically demonstrate the effectiveness of our approach compared to point-estimated networks and methods that use less expressive posterior approximations over the full network.

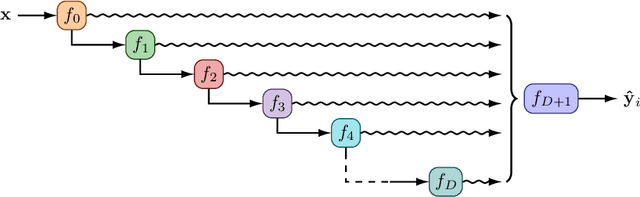
Depth Uncertainty in Neural Networks

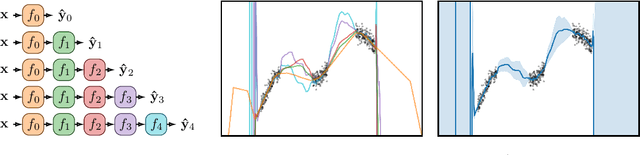
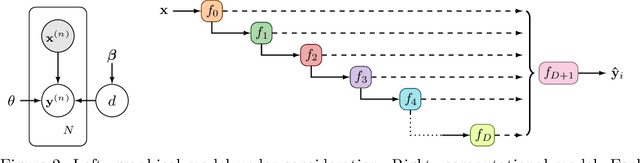
Existing methods for estimating uncertainty in deep learning tend to require multiple forward passes, making them unsuitable for applications where computational resources are limited. To solve this, we perform probabilistic reasoning over the depth of neural networks. Different depths correspond to subnetworks which share weights and whose predictions are combined via marginalisation, yielding model uncertainty. By exploiting the sequential structure of feed-forward networks, we are able to both evaluate our training objective and make predictions with a single forward pass. We validate our approach on real-world regression and image classification tasks. Our approach provides uncertainty calibration, robustness to dataset shift, and accuracies competitive with more computationally expensive baselines.

Getting a CLUE: A Method for Explaining Uncertainty Estimates

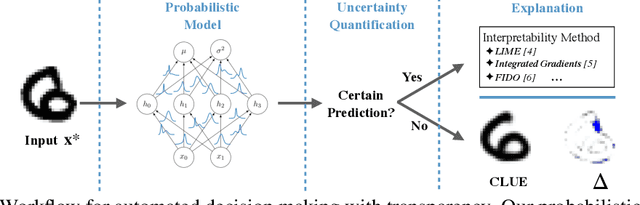
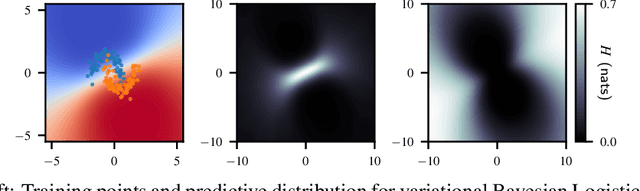
Both uncertainty estimation and interpretability are important factors for trustworthy machine learning systems. However, there is little work at the intersection of these two areas. We address this gap by proposing a novel method for interpreting uncertainty estimates from differentiable probabilistic models, like Bayesian Neural Networks (BNNs). Our method, Counterfactual Latent Uncertainty Explanations (CLUE), indicates how to change an input, while keeping it on the data manifold, such that a BNN becomes more confident about the input's prediction. We validate CLUE through 1) a novel framework for evaluating counterfactual explanations of uncertainty, 2) a series of ablation experiments, and 3) a user study. Our experiments show that CLUE outperforms baselines and enables practitioners to better understand which input patterns are responsible for predictive uncertainty.

Variational Depth Search in ResNets

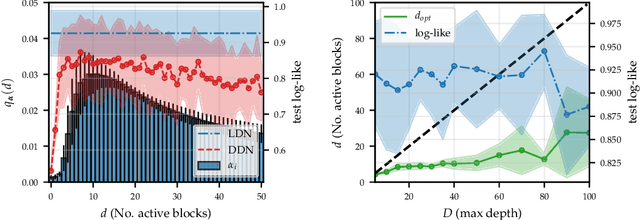
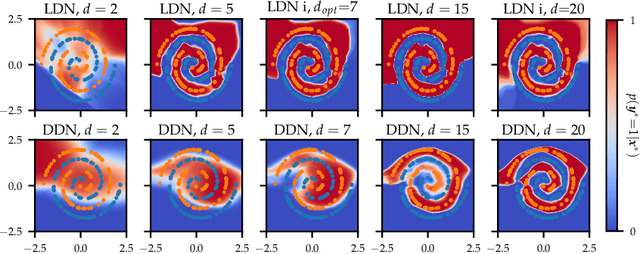
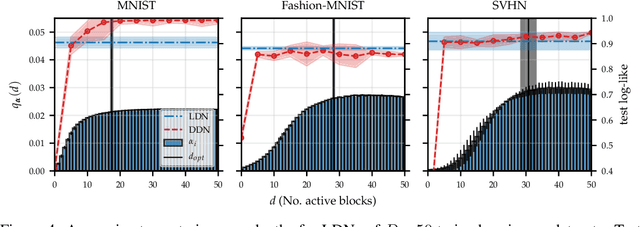
One-shot neural architecture search allows joint learning of weights and network architecture, reducing computational cost. We limit our search space to the depth of residual networks and formulate an analytically tractable variational objective that allows for obtaining an unbiased approximate posterior over depths in one-shot. We propose a heuristic to prune our networks based on this distribution. We compare our proposed method against manual search over network depths on the MNIST, Fashion-MNIST, SVHN datasets. We find that pruned networks do not incur a loss in predictive performance, obtaining accuracies competitive with unpruned networks. Marginalising over depth allows us to obtain better-calibrated test-time uncertainty estimates than regular networks, in a single forward pass.