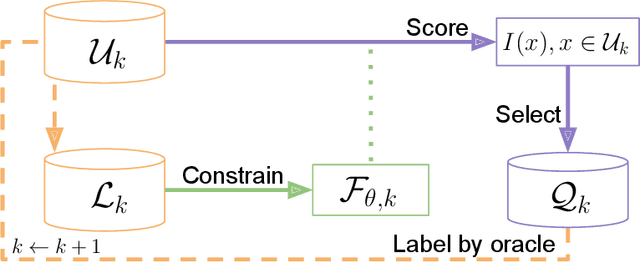
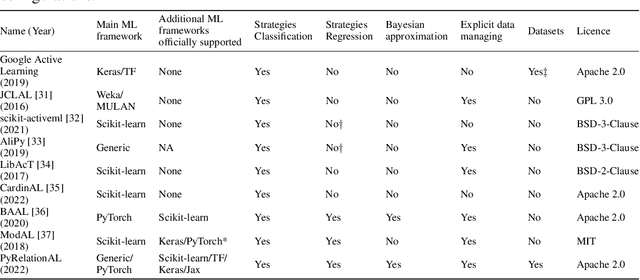
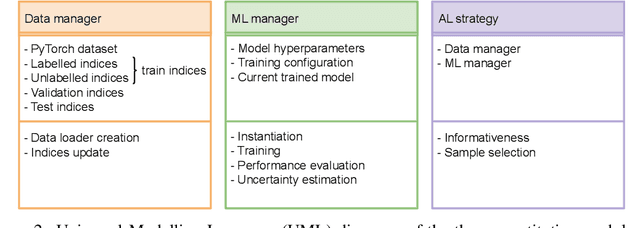
PyRelationAL: A Library for Active Learning Research and Development

In constrained real-world scenarios where it is challenging or costly to generate data, disciplined methods for acquiring informative new data points are of fundamental importance for the efficient training of machine learning (ML) models. Active learning (AL) is a subfield of ML focused on the development of methods to iteratively and economically acquire data through strategically querying new data points that are the most useful for a particular task. Here, we introduce PyRelationAL, an open source library for AL research. We describe a modular toolkit that is compatible with diverse ML frameworks (e.g. PyTorch, Scikit-Learn, TensorFlow, JAX). Furthermore, to help accelerate research and development in the field, the library implements a number of published methods and provides API access to wide-ranging benchmark datasets and AL task configurations based on existing literature. The library is supplemented by an expansive set of tutorials, demos, and documentation to help users get started. We perform experiments on the PyRelationAL collection of benchmark datasets and showcase the considerable economies that AL can provide. PyRelationAL is maintained using modern software engineering practices - with an inclusive contributor code of conduct - to promote long term library quality and utilisation.

RECOVER: sequential model optimization platform for combination drug repurposing identifies novel synergistic compounds in vitro

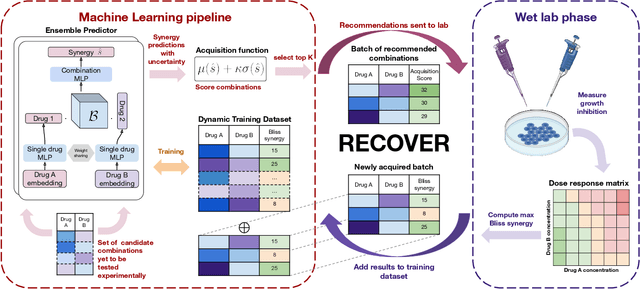
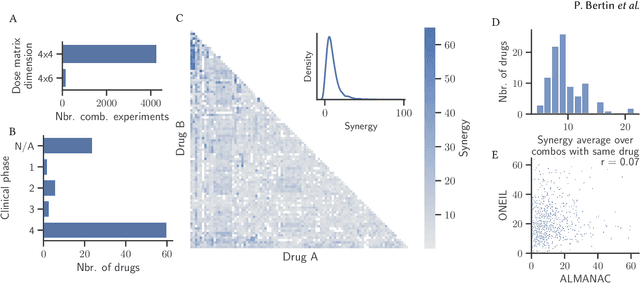
Selecting optimal drug repurposing combinations for further preclinical development is a challenging technical feat. Due to the toxicity of many therapeutic agents (e.g., chemotherapy), practitioners have favoured selection of synergistic compounds whereby lower doses can be used whilst maintaining high efficacy. For a fixed small molecule library, an exhaustive combinatorial chemical screen becomes infeasible to perform for academic and industry laboratories alike. Deep learning models have achieved state-of-the-art results in silico for the prediction of synergy scores. However, databases of drug combinations are highly biased towards synergistic agents and these results do not necessarily generalise out of distribution. We employ a sequential model optimization search applied to a deep learning model to quickly discover highly synergistic drug combinations active against a cancer cell line, while requiring substantially less screening than an exhaustive evaluation. Through iteratively adapting the model to newly acquired data, after only 3 rounds of ML-guided experimentation (including a calibration round), we find that the set of combinations queried by our model is enriched for highly synergistic combinations. Remarkably, we rediscovered a synergistic drug combination that was later confirmed to be under study within clinical trials.

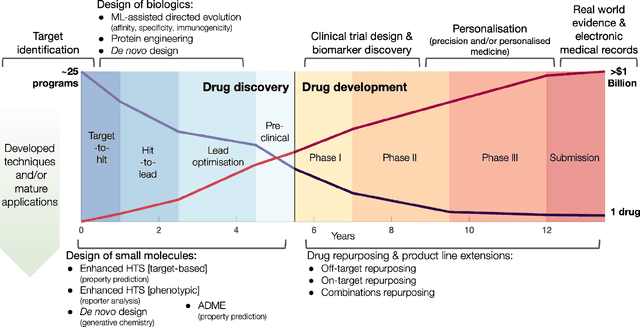
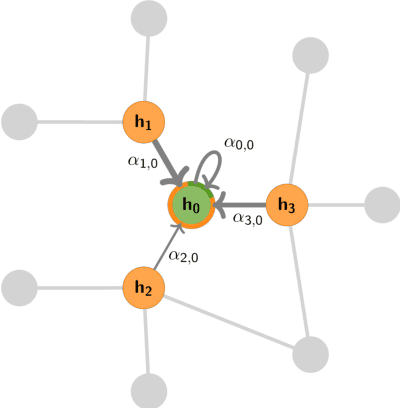
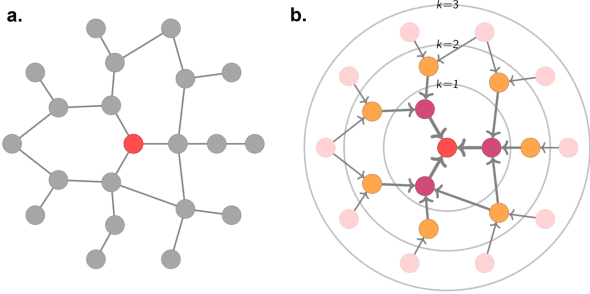
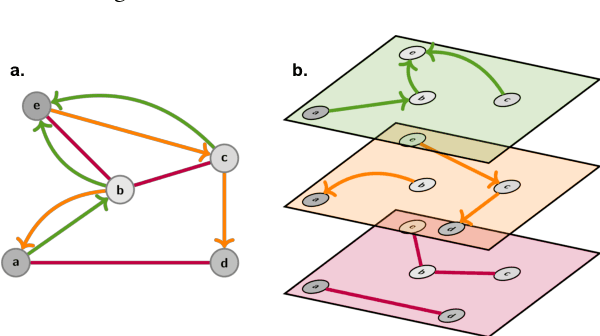
Utilising Graph Machine Learning within Drug Discovery and Development

Graph Machine Learning (GML) is receiving growing interest within the pharmaceutical and biotechnology industries for its ability to model biomolecular structures, the functional relationships between them, and integrate multi-omic datasets - amongst other data types. Herein, we present a multidisciplinary academic-industrial review of the topic within the context of drug discovery and development. After introducing key terms and modelling approaches, we move chronologically through the drug development pipeline to identify and summarise work incorporating: target identification, design of small molecules and biologics, and drug repurposing. Whilst the field is still emerging, key milestones including repurposed drugs entering in vivo studies, suggest graph machine learning will become a modelling framework of choice within biomedical machine learning.

Sparse Dynamic Distribution Decomposition: Efficient Integration of Trajectory and Snapshot Time Series Data

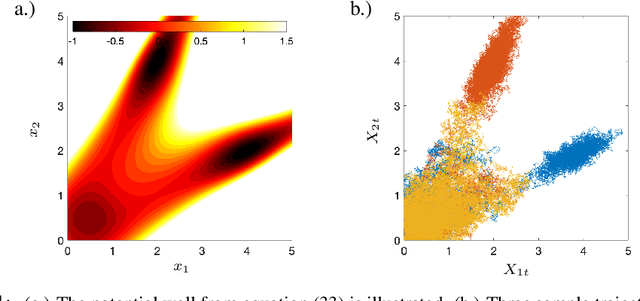
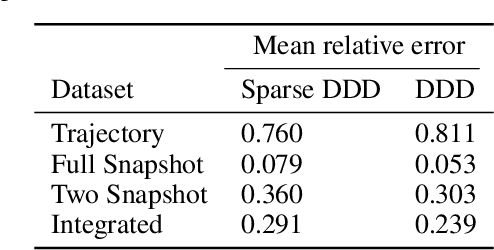
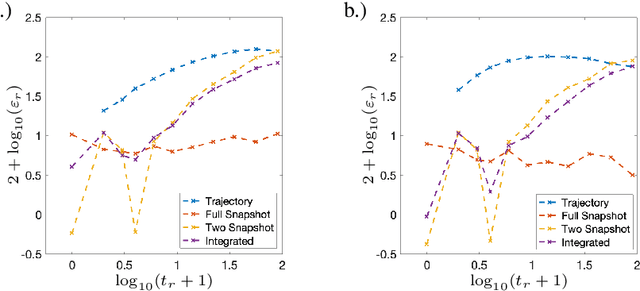
Dynamic Distribution Decomposition (DDD) was introduced in Taylor-King et. al. (PLOS Comp Biol, 2020) as a variation on Dynamic Mode Decomposition. In brief, by using basis functions over a continuous state space, DDD allows for the fitting of continuous-time Markov chains over these basis functions and as a result continuously maps between distributions. The number of parameters in DDD scales by the square of the number of basis functions; we reformulate the problem and restrict the method to compact basis functions which leads to the inference of sparse matrices only -- hence reducing the number of parameters. Finally, we demonstrate how DDD is suitable to integrate both trajectory time series (paired between subsequent time points) and snapshot time series (unpaired time points). Methods capable of integrating both scenarios are particularly relevant for the analysis of biomedical data, whereby studies observe population at fixed time points (snapshots) and individual patient journeys with repeated follow ups (trajectories).

Mathematical Modelling of Turning Delays in Swarm Robotics

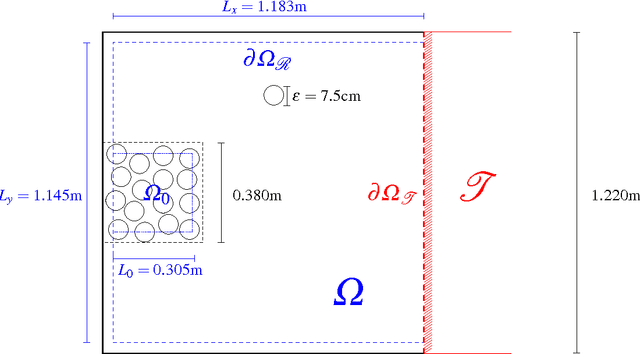
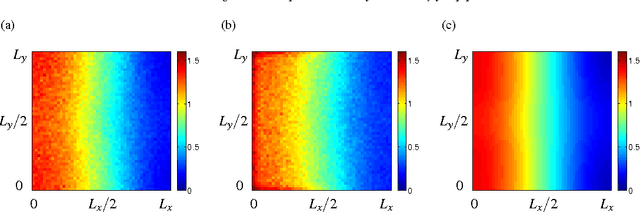
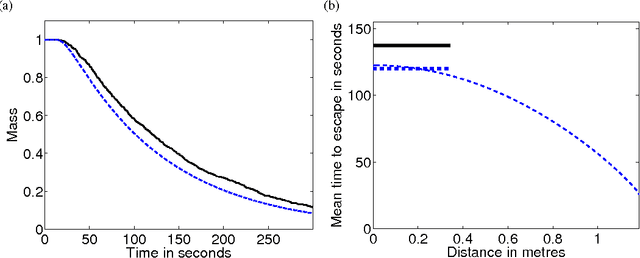
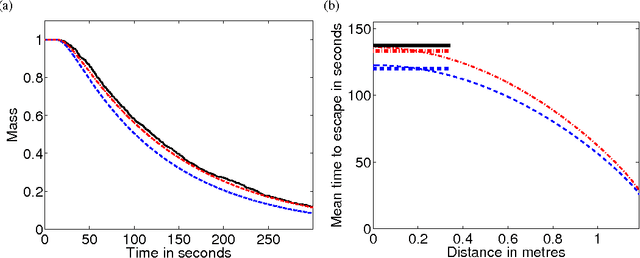
We investigate the effect of turning delays on the behaviour of groups of differential wheeled robots and show that the group-level behaviour can be described by a transport equation with a suitably incorporated delay. The results of our mathematical analysis are supported by numerical simulations and experiments with e-puck robots. The experimental quantity we compare to our revised model is the mean time for robots to find the target area in an unknown environment. The transport equation with delay better predicts the mean time to find the target than the standard transport equation without delay.