Sample-Based Hybrid Mode Control: Asymptotically Optimal Switching of Algorithmic and Non-Differentiable Control Modes

This paper investigates a sample-based solution to the hybrid mode control problem across non-differentiable and algorithmic hybrid modes. Our approach reasons about a set of hybrid control modes as an integer-based optimization problem where we select what mode to apply, when to switch to another mode, and the duration for which we are in a given control mode. A sample-based variation is derived to efficiently search the integer domain for optimal solutions. We find our formulation yields strong performance guarantees that can be applied to a number of robotics-related tasks. In addition, our approach is able to synthesize complex algorithms and policies to compound behaviors and achieve challenging tasks. Last, we demonstrate the effectiveness of our approach in real-world robotic examples that require reactive switching between long-term planning and high-frequency control.

Behavior Synthesis via Contact-Aware Fisher Information Maximization

Contact dynamics hold immense amounts of information that can improve a robot's ability to characterize and learn about objects in their environment through interactions. However, collecting information-rich contact data is challenging due to its inherent sparsity and non-smooth nature, requiring an active approach to maximize the utility of contacts for learning. In this work, we investigate an optimal experimental design approach to synthesize robot behaviors that produce contact-rich data for learning. Our approach derives a contact-aware Fisher information measure that characterizes information-rich contact behaviors that improve parameter learning. We observe emergent robot behaviors that are able to excite contact interactions that efficiently learns object parameters across a range of parameter learning examples. Last, we demonstrate the utility of contact-awareness for learning parameters through contact-seeking behaviors on several robotic experiments.

Accelerating Visual-Policy Learning through Parallel Differentiable Simulation

In this work, we propose a computationally efficient algorithm for visual policy learning that leverages differentiable simulation and first-order analytical policy gradients. Our approach decouple the rendering process from the computation graph, enabling seamless integration with existing differentiable simulation ecosystems without the need for specialized differentiable rendering software. This decoupling not only reduces computational and memory overhead but also effectively attenuates the policy gradient norm, leading to more stable and smoother optimization. We evaluate our method on standard visual control benchmarks using modern GPU-accelerated simulation. Experiments show that our approach significantly reduces wall-clock training time and consistently outperforms all baseline methods in terms of final returns. Notably, on complex tasks such as humanoid locomotion, our method achieves a $4\times$ improvement in final return, and successfully learns a humanoid running policy within 4 hours on a single GPU.

Ergodic Exploration over Meshable Surfaces

Robotic search and rescue, exploration, and inspection require trajectory planning across a variety of domains. A popular approach to trajectory planning for these types of missions is ergodic search, which biases a trajectory to spend time in parts of the exploration domain that are believed to contain more information. Most prior work on ergodic search has been limited to searching simple surfaces, like a 2D Euclidean plane or a sphere, as they rely on projecting functions defined on the exploration domain onto analytically obtained Fourier basis functions. In this paper, we extend ergodic search to any surface that can be approximated by a triangle mesh. The basis functions are approximated through finite element methods on a triangle mesh of the domain. We formally prove that this approximation converges to the continuous case as the mesh approximation converges to the true domain. We demonstrate that on domains where analytical basis functions are available (plane, sphere), the proposed method obtains equivalent results, and while on other domains (torus, bunny, wind turbine), the approach is versatile enough to still search effectively. Lastly, we also compare with an existing ergodic search technique that can handle complex domains and show that our method results in a higher quality exploration.

Is Bellman Equation Enough for Learning Control?

The Bellman equation and its continuous-time counterpart, the Hamilton-Jacobi-Bellman (HJB) equation, serve as necessary conditions for optimality in reinforcement learning and optimal control. While the value function is known to be the unique solution to the Bellman equation in tabular settings, we demonstrate that this uniqueness fails to hold in continuous state spaces. Specifically, for linear dynamical systems, we prove the Bellman equation admits at least $\binom{2n}{n}$ solutions, where $n$ is the state dimension. Crucially, only one of these solutions yields both an optimal policy and a stable closed-loop system. We then demonstrate a common failure mode in value-based methods: convergence to unstable solutions due to the exponential imbalance between admissible and inadmissible solutions. Finally, we introduce a positive-definite neural architecture that guarantees convergence to the stable solution by construction to address this issue.

Multi-Agent Ergodic Exploration under Smoke-Based, Time-Varying Sensor Visibility Constraints

In this work, we consider the problem of multi-agent informative path planning (IPP) for robots whose sensor visibility continuously changes as a consequence of a time-varying natural phenomenon. We leverage ergodic trajectory optimization (ETO), which generates paths such that the amount of time an agent spends in an area is proportional to the expected information in that area. We focus specifically on the problem of multi-agent drone search of a wildfire, where we use the time-varying environmental process of smoke diffusion to construct a sensor visibility model. This sensor visibility model is used to repeatedly calculate an expected information distribution (EID) to be used in the ETO algorithm. Our experiments show that our exploration method achieves improved information gathering over both baseline search methods and naive ergodic search formulations.

Exciting Contact Modes in Differentiable Simulations for Robot Learning

In this paper, we explore an approach to actively plan and excite contact modes in differentiable simulators as a means to tighten the sim-to-real gap. We propose an optimal experimental design approach derived from information-theoretic methods to identify and search for information-rich contact modes through the use of contact-implicit optimization. We demonstrate our approach on a robot parameter estimation problem with unknown inertial and kinematic parameters which actively seeks contacts with a nearby surface. We show that our approach improves the identification of unknown parameter estimates over experimental runs by an estimate error reduction of at least $\sim 84\%$ when compared to a random sampling baseline, with significantly higher information gains.

Ergodic Trajectory Optimization on Generalized Domains Using Maximum Mean Discrepancy

We present a novel formulation of ergodic trajectory optimization that can be specified over general domains using kernel maximum mean discrepancy. Ergodic trajectory optimization is an effective approach that generates coverage paths for problems related to robotic inspection, information gathering problems, and search and rescue. These optimization schemes compel the robot to spend time in a region proportional to the expected utility of visiting that region. Current methods for ergodic trajectory optimization rely on domain-specific knowledge, e.g., a defined utility map, and well-defined spatial basis functions to produce ergodic trajectories. Here, we present a generalization of ergodic trajectory optimization based on maximum mean discrepancy that requires only samples from the search domain. We demonstrate the ability of our approach to produce coverage trajectories on a variety of problem domains including robotic inspection of objects with differential kinematics constraints and on Lie groups without having access to domain specific knowledge. Furthermore, we show favorable computational scaling compared to existing state-of-the-art methods for ergodic trajectory optimization with a trade-off between domain specific knowledge and computational scaling, thus extending the versatility of ergodic coverage on a wider application domain.

Measure Preserving Flows for Ergodic Search in Convoluted Environments

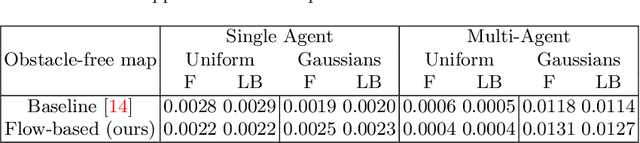
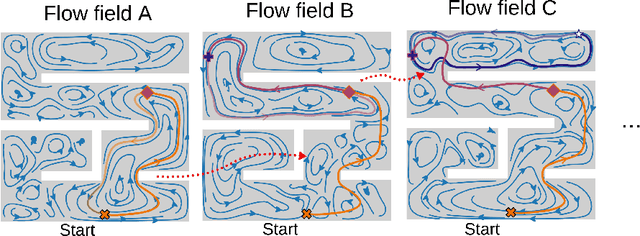
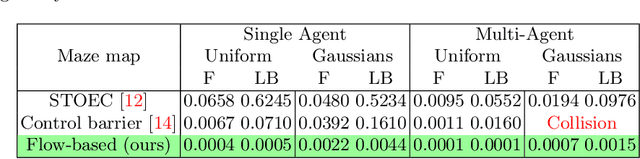
Autonomous robotic search has important applications in robotics, such as the search for signs of life after a disaster. When \emph{a priori} information is available, for example in the form of a distribution, a planner can use that distribution to guide the search. Ergodic search is one method that uses the information distribution to generate a trajectory that minimizes the ergodic metric, in that it encourages the robot to spend more time in regions with high information and proportionally less time in the remaining regions. Unfortunately, prior works in ergodic search do not perform well in complex environments with obstacles such as a building's interior or a maze. To address this, our work presents a modified ergodic metric using the Laplace-Beltrami eigenfunctions to capture map geometry and obstacle locations within the ergodic metric. Further, we introduce an approach to generate trajectories that minimize the ergodic metric while guaranteeing obstacle avoidance using measure-preserving vector fields. Finally, we leverage the divergence-free nature of these vector fields to generate collision-free trajectories for multiple agents. We demonstrate our approach via simulations with single and multi-agent systems on maps representing interior hallways and long corridors with non-uniform information distribution. In particular, we illustrate the generation of feasible trajectories in complex environments where prior methods fail.

Koopman Operators in Robot Learning

Koopman operator theory offers a rigorous treatment of dynamics and has been emerging as a powerful modeling and learning-based control method enabling significant advancements across various domains of robotics. Due to its ability to represent nonlinear dynamics as a linear operator, Koopman theory offers a fresh lens through which to understand and tackle the modeling and control of complex robotic systems. Moreover, it enables incremental updates and is computationally inexpensive making it particularly appealing for real-time applications and online active learning. This review comprehensively presents recent research results on advancing Koopman operator theory across diverse domains of robotics, encompassing aerial, legged, wheeled, underwater, soft, and manipulator robotics. Furthermore, it offers practical tutorials to help new users get started as well as a treatise of more advanced topics leading to an outlook on future directions and open research questions. Taken together, these provide insights into the potential evolution of Koopman theory as applied to the field of robotics.