Improved machine learning algorithm for predicting ground state properties

Finding the ground state of a quantum many-body system is a fundamental problem in quantum physics. In this work, we give a classical machine learning (ML) algorithm for predicting ground state properties with an inductive bias encoding geometric locality. The proposed ML model can efficiently predict ground state properties of an $n$-qubit gapped local Hamiltonian after learning from only $\mathcal{O}(\log(n))$ data about other Hamiltonians in the same quantum phase of matter. This improves substantially upon previous results that require $\mathcal{O}(n^c)$ data for a large constant $c$. Furthermore, the training and prediction time of the proposed ML model scale as $\mathcal{O}(n \log n)$ in the number of qubits $n$. Numerical experiments on physical systems with up to 45 qubits confirm the favorable scaling in predicting ground state properties using a small training dataset.

Hardware-efficient learning of quantum many-body states

Efficient characterization of highly entangled multi-particle systems is an outstanding challenge in quantum science. Recent developments have shown that a modest number of randomized measurements suffices to learn many properties of a quantum many-body system. However, implementing such measurements requires complete control over individual particles, which is unavailable in many experimental platforms. In this work, we present rigorous and efficient algorithms for learning quantum many-body states in systems with any degree of control over individual particles, including when every particle is subject to the same global field and no additional ancilla particles are available. We numerically demonstrate the effectiveness of our algorithms for estimating energy densities in a U(1) lattice gauge theory and classifying topological order using very limited measurement capabilities.

Learning to predict arbitrary quantum processes

We present an efficient machine learning (ML) algorithm for predicting any unknown quantum process $\mathcal{E}$ over $n$ qubits. For a wide range of distributions $\mathcal{D}$ on arbitrary $n$-qubit states, we show that this ML algorithm can learn to predict any local property of the output from the unknown process $\mathcal{E}$, with a small average error over input states drawn from $\mathcal{D}$. The ML algorithm is computationally efficient even when the unknown process is a quantum circuit with exponentially many gates. Our algorithm combines efficient procedures for learning properties of an unknown state and for learning a low-degree approximation to an unknown observable. The analysis hinges on proving new norm inequalities, including a quantum analogue of the classical Bohnenblust-Hille inequality, which we derive by giving an improved algorithm for optimizing local Hamiltonians. Overall, our results highlight the potential for ML models to predict the output of complex quantum dynamics much faster than the time needed to run the process itself.

The Complexity of NISQ

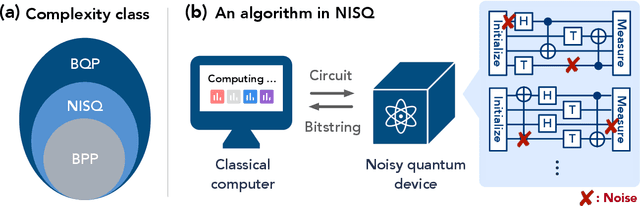
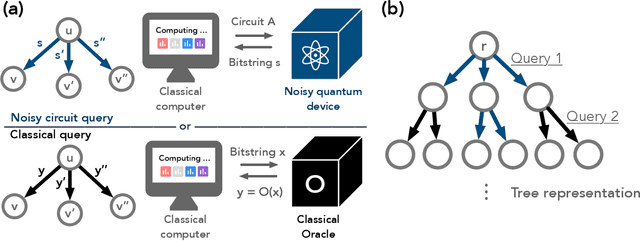
The recent proliferation of NISQ devices has made it imperative to understand their computational power. In this work, we define and study the complexity class $\textsf{NISQ} $, which is intended to encapsulate problems that can be efficiently solved by a classical computer with access to a NISQ device. To model existing devices, we assume the device can (1) noisily initialize all qubits, (2) apply many noisy quantum gates, and (3) perform a noisy measurement on all qubits. We first give evidence that $\textsf{BPP}\subsetneq \textsf{NISQ}\subsetneq \textsf{BQP}$, by demonstrating super-polynomial oracle separations among the three classes, based on modifications of Simon's problem. We then consider the power of $\textsf{NISQ}$ for three well-studied problems. For unstructured search, we prove that $\textsf{NISQ}$ cannot achieve a Grover-like quadratic speedup over $\textsf{BPP}$. For the Bernstein-Vazirani problem, we show that $\textsf{NISQ}$ only needs a number of queries logarithmic in what is required for $\textsf{BPP}$. Finally, for a quantum state learning problem, we prove that $\textsf{NISQ}$ is exponentially weaker than classical computation with access to noiseless constant-depth quantum circuits.

Learning many-body Hamiltonians with Heisenberg-limited scaling

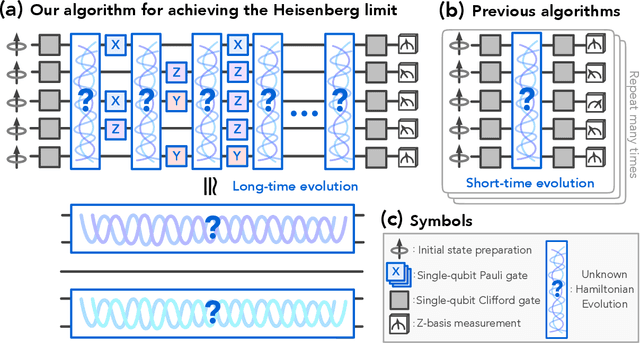
Learning a many-body Hamiltonian from its dynamics is a fundamental problem in physics. In this work, we propose the first algorithm to achieve the Heisenberg limit for learning an interacting $N$-qubit local Hamiltonian. After a total evolution time of $\mathcal{O}(\epsilon^{-1})$, the proposed algorithm can efficiently estimate any parameter in the $N$-qubit Hamiltonian to $\epsilon$-error with high probability. The proposed algorithm is robust against state preparation and measurement error, does not require eigenstates or thermal states, and only uses $\mathrm{polylog}(\epsilon^{-1})$ experiments. In contrast, the best previous algorithms, such as recent works using gradient-based optimization or polynomial interpolation, require a total evolution time of $\mathcal{O}(\epsilon^{-2})$ and $\mathcal{O}(\epsilon^{-2})$ experiments. Our algorithm uses ideas from quantum simulation to decouple the unknown $N$-qubit Hamiltonian $H$ into noninteracting patches, and learns $H$ using a quantum-enhanced divide-and-conquer approach. We prove a matching lower bound to establish the asymptotic optimality of our algorithm.

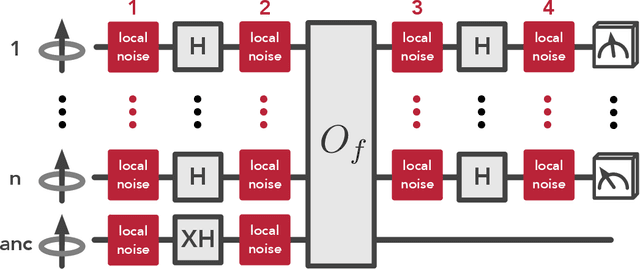
Foundations for learning from noisy quantum experiments

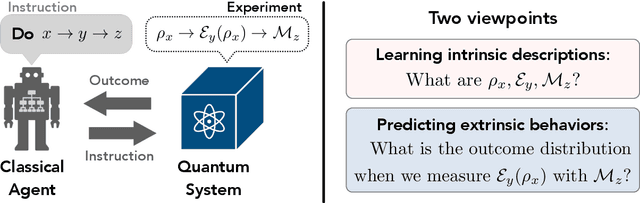
Understanding what can be learned from experiments is central to scientific progress. In this work, we use a learning-theoretic perspective to study the task of learning physical operations in a quantum machine when all operations (state preparation, dynamics, and measurement) are a priori unknown. We prove that, without any prior knowledge, if one can explore the full quantum state space by composing the operations, then every operation can be learned. When one cannot explore the full state space but all operations are approximately known and noise in Clifford gates is gate-independent, we find an efficient algorithm for learning all operations up to a single unlearnable parameter characterizing the fidelity of the initial state. For learning a noise channel on Clifford gates to a fixed accuracy, our algorithm uses quadratically fewer experiments than previously known protocols. Under more general conditions, the true description of the noise can be unlearnable; for example, we prove that no benchmarking protocol can learn gate-dependent Pauli noise on Clifford+T gates even under perfect state preparation and measurement. Despite not being able to learn the noise, we show that a noisy quantum computer that performs entangled measurements on multiple copies of an unknown state can yield a large advantage in learning properties of the state compared to a noiseless device that measures individual copies and then processes the measurement data using a classical computer. Concretely, we prove that noisy quantum computers with two-qubit gate error rate $\epsilon$ can achieve a learning task using $N$ copies of the state, while $N^{\Omega(1/\epsilon)}$ copies are required classically.

Dynamical simulation via quantum machine learning with provable generalization

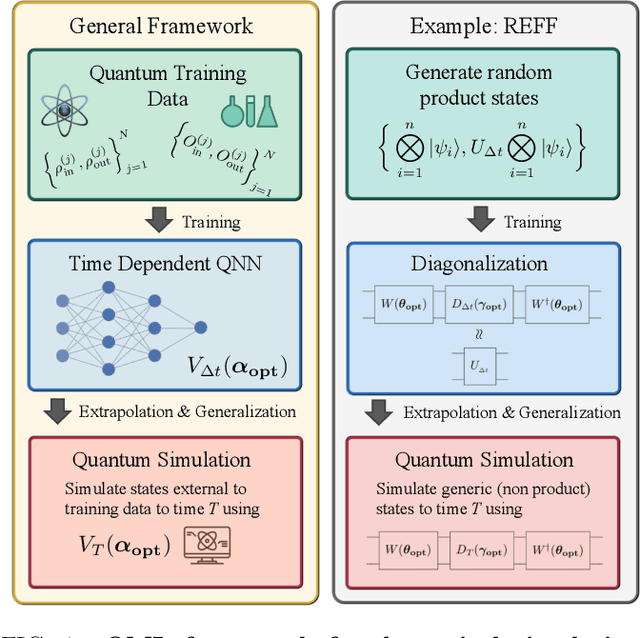
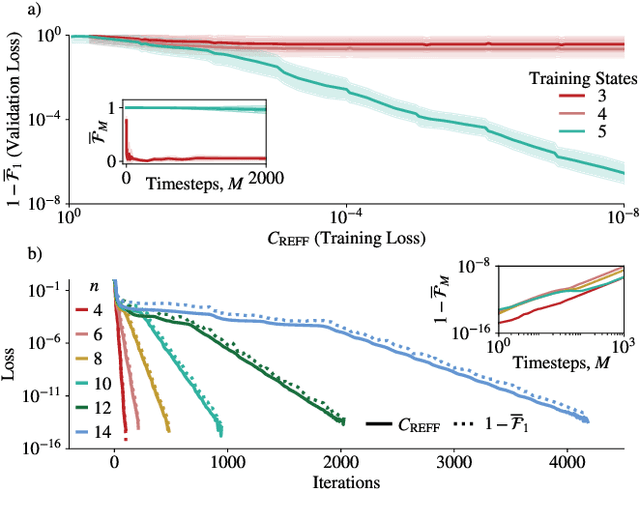
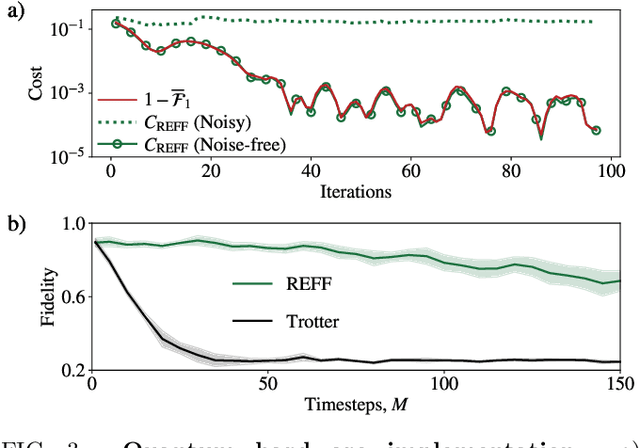
Much attention has been paid to dynamical simulation and quantum machine learning (QML) independently as applications for quantum advantage, while the possibility of using QML to enhance dynamical simulations has not been thoroughly investigated. Here we develop a framework for using QML methods to simulate quantum dynamics on near-term quantum hardware. We use generalization bounds, which bound the error a machine learning model makes on unseen data, to rigorously analyze the training data requirements of an algorithm within this framework. This provides a guarantee that our algorithm is resource-efficient, both in terms of qubit and data requirements. Our numerics exhibit efficient scaling with problem size, and we simulate 20 times longer than Trotterization on IBMQ-Bogota.

Out-of-distribution generalization for learning quantum dynamics

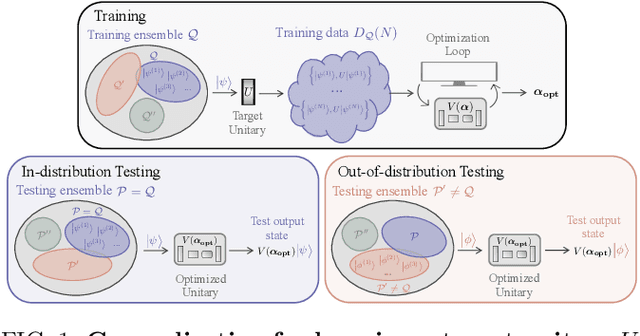
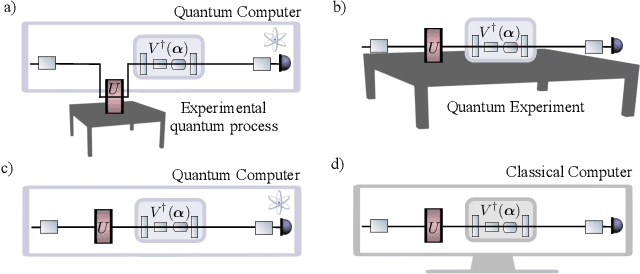
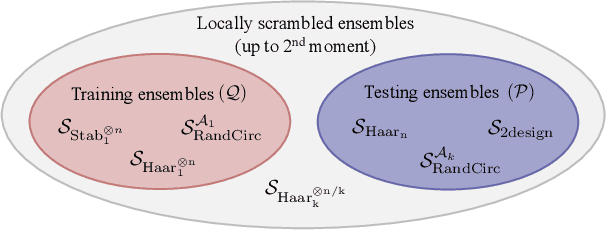
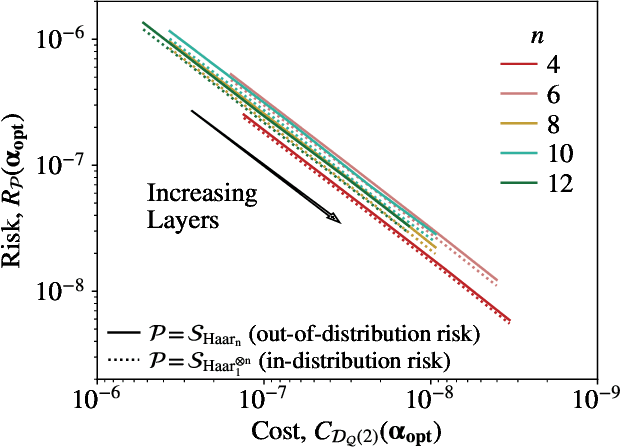
Generalization bounds are a critical tool to assess the training data requirements of Quantum Machine Learning (QML). Recent work has established guarantees for in-distribution generalization of quantum neural networks (QNNs), where training and testing data are assumed to be drawn from the same data distribution. However, there are currently no results on out-of-distribution generalization in QML, where we require a trained model to perform well even on data drawn from a distribution different from the training distribution. In this work, we prove out-of-distribution generalization for the task of learning an unknown unitary using a QNN and for a broad class of training and testing distributions. In particular, we show that one can learn the action of a unitary on entangled states using only product state training data. We numerically illustrate this by showing that the evolution of a Heisenberg spin chain can be learned using only product training states. Since product states can be prepared using only single-qubit gates, this advances the prospects of learning quantum dynamics using near term quantum computers and quantum experiments, and further opens up new methods for both the classical and quantum compilation of quantum circuits.

Revisiting dequantization and quantum advantage in learning tasks

It has been shown that the apparent advantage of some quantum machine learning algorithms may be efficiently replicated using classical algorithms with suitable data access -- a process known as dequantization. Existing works on dequantization compare quantum algorithms which take copies of an n-qubit quantum state $|x\rangle = \sum_{i} x_i |i\rangle$ as input to classical algorithms which have sample and query (SQ) access to the vector $x$. In this note, we prove that classical algorithms with SQ access can accomplish some learning tasks exponentially faster than quantum algorithms with quantum state inputs. Because classical algorithms are a subset of quantum algorithms, this demonstrates that SQ access can sometimes be significantly more powerful than quantum state inputs. Our findings suggest that the absence of exponential quantum advantage in some learning tasks may be due to SQ access being too powerful relative to quantum state inputs. If we compare quantum algorithms with quantum state inputs to classical algorithms with access to measurement data on quantum states, the landscape of quantum advantage can be dramatically different. We remark that when the quantum states are constructed from exponential-size classical data, comparing SQ access and quantum state inputs is appropriate since both require exponential time to prepare.

Quantum advantage in learning from experiments

Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.