Stone Soup Multi-Target Tracking Feature Extraction For Autonomous Search And Track In Deep Reinforcement Learning Environment

Management of sensing resources is a non-trivial problem for future military air assets with future systems deploying heterogeneous sensors to generate information of the battlespace. Machine learning techniques including deep reinforcement learning (DRL) have been identified as promising approaches, but require high-fidelity training environments and feature extractors to generate information for the agent. This paper presents a deep reinforcement learning training approach, utilising the Stone Soup tracking framework as a feature extractor to train an agent for a sensor management task. A general framework for embedding Stone Soup tracker components within a Gymnasium environment is presented, enabling fast and configurable tracker deployments for RL training using Stable Baselines3. The approach is demonstrated in a sensor management task where an agent is trained to search and track a region of airspace utilising track lists generated from Stone Soup trackers. A sample implementation using three neural network architectures in a search-and-track scenario demonstrates the approach and shows that RL agents can outperform simple sensor search and track policies when trained within the Gymnasium and Stone Soup environment.

Multi-Target Radar Search and Track Using Sequence-Capable Deep Reinforcement Learning

The research addresses sensor task management for radar systems, focusing on efficiently searching and tracking multiple targets using reinforcement learning. The approach develops a 3D simulation environment with an active electronically scanned array radar, using a multi-target tracking algorithm to improve observation data quality. Three neural network architectures were compared including an approach using fated recurrent units with multi-headed self-attention. Two pre-training techniques were applied: behavior cloning to approximate a random search strategy and an auto-encoder to pre-train the feature extractor. Experimental results revealed that search performance was relatively consistent across most methods. The real challenge emerged in simultaneously searching and tracking targets. The multi-headed self-attention architecture demonstrated the most promising results, highlighting the potential of sequence-capable architectures in handling dynamic tracking scenarios. The key contribution lies in demonstrating how reinforcement learning can optimize sensor management, potentially improving radar systems' ability to identify and track multiple targets in complex environments.

The power and limitations of learning quantum dynamics incoherently

Quantum process learning is emerging as an important tool to study quantum systems. While studied extensively in coherent frameworks, where the target and model system can share quantum information, less attention has been paid to whether the dynamics of quantum systems can be learned without the system and target directly interacting. Such incoherent frameworks are practically appealing since they open up methods of transpiling quantum processes between the different physical platforms without the need for technically challenging hybrid entanglement schemes. Here we provide bounds on the sample complexity of learning unitary processes incoherently by analyzing the number of measurements that are required to emulate well-established coherent learning strategies. We prove that if arbitrary measurements are allowed, then any efficiently representable unitary can be efficiently learned within the incoherent framework; however, when restricted to shallow-depth measurements only low-entangling unitaries can be learned. We demonstrate our incoherent learning algorithm for low entangling unitaries by successfully learning a 16-qubit unitary on \texttt{ibmq\_kolkata}, and further demonstrate the scalabilty of our proposed algorithm through extensive numerical experiments.

Dynamical simulation via quantum machine learning with provable generalization

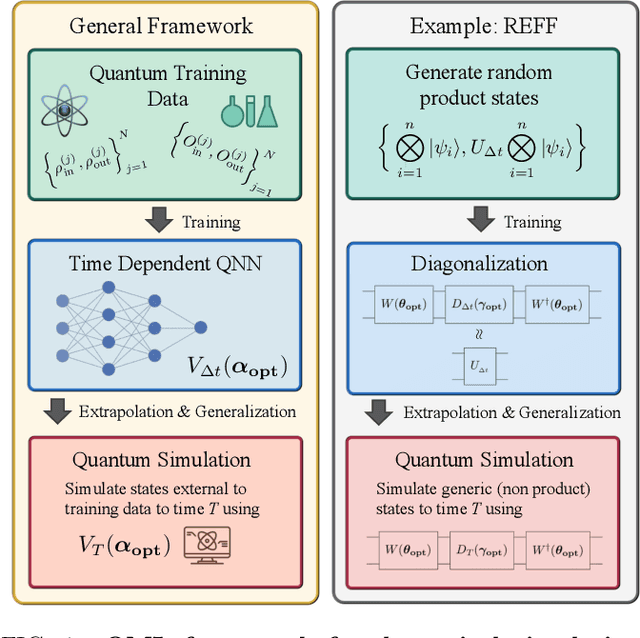
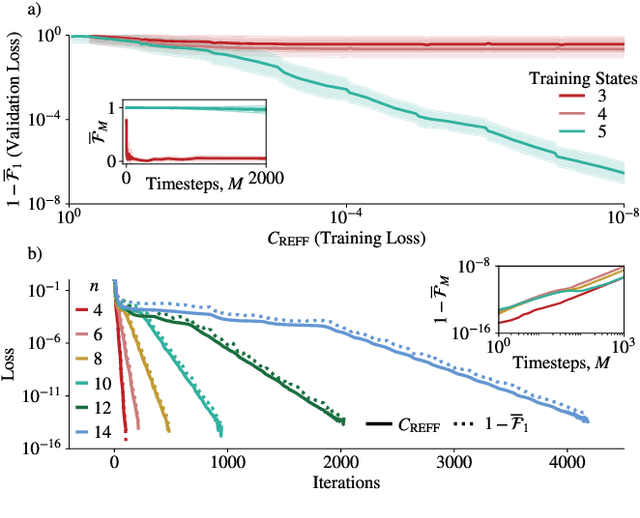
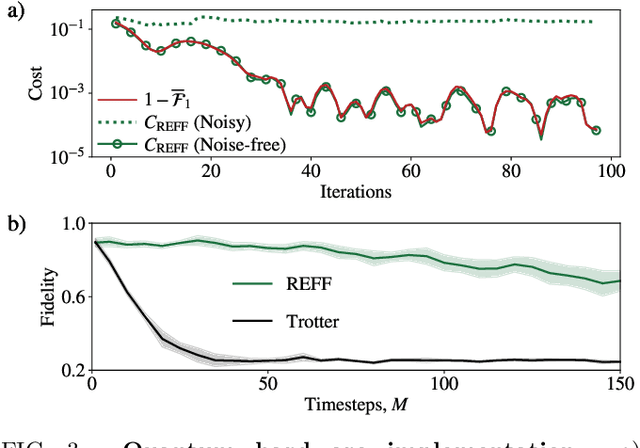
Much attention has been paid to dynamical simulation and quantum machine learning (QML) independently as applications for quantum advantage, while the possibility of using QML to enhance dynamical simulations has not been thoroughly investigated. Here we develop a framework for using QML methods to simulate quantum dynamics on near-term quantum hardware. We use generalization bounds, which bound the error a machine learning model makes on unseen data, to rigorously analyze the training data requirements of an algorithm within this framework. This provides a guarantee that our algorithm is resource-efficient, both in terms of qubit and data requirements. Our numerics exhibit efficient scaling with problem size, and we simulate 20 times longer than Trotterization on IBMQ-Bogota.

Out-of-distribution generalization for learning quantum dynamics

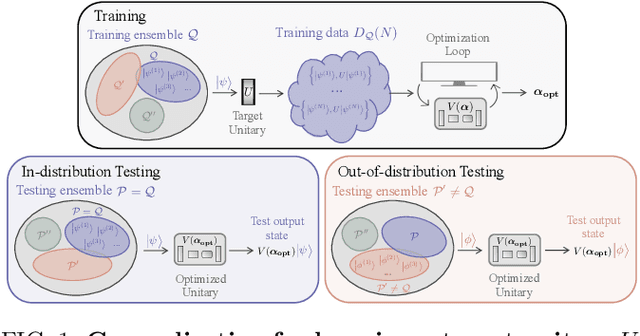
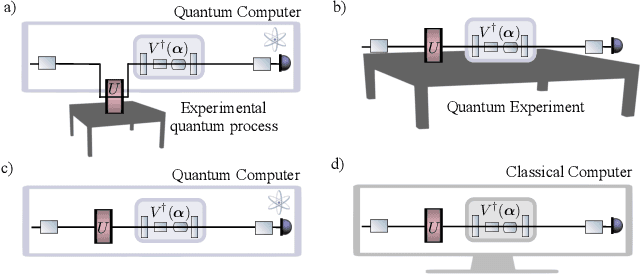
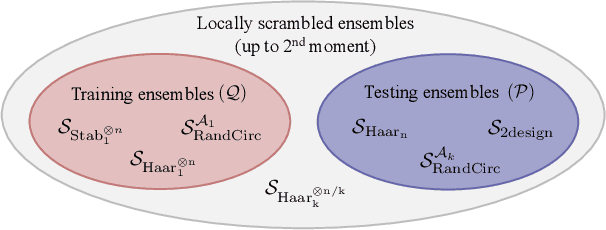
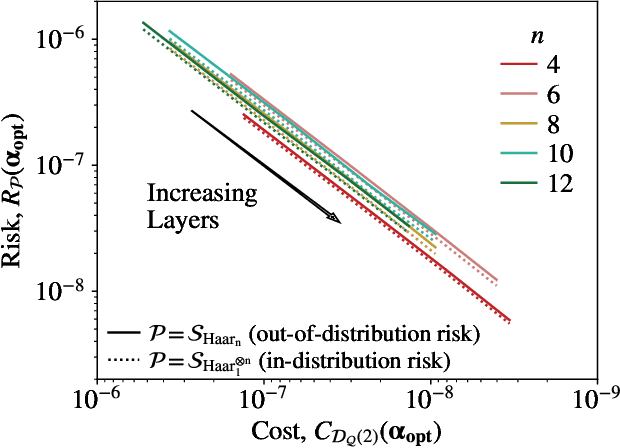
Generalization bounds are a critical tool to assess the training data requirements of Quantum Machine Learning (QML). Recent work has established guarantees for in-distribution generalization of quantum neural networks (QNNs), where training and testing data are assumed to be drawn from the same data distribution. However, there are currently no results on out-of-distribution generalization in QML, where we require a trained model to perform well even on data drawn from a distribution different from the training distribution. In this work, we prove out-of-distribution generalization for the task of learning an unknown unitary using a QNN and for a broad class of training and testing distributions. In particular, we show that one can learn the action of a unitary on entangled states using only product state training data. We numerically illustrate this by showing that the evolution of a Heisenberg spin chain can be learned using only product training states. Since product states can be prepared using only single-qubit gates, this advances the prospects of learning quantum dynamics using near term quantum computers and quantum experiments, and further opens up new methods for both the classical and quantum compilation of quantum circuits.

Long-time simulations with high fidelity on quantum hardware

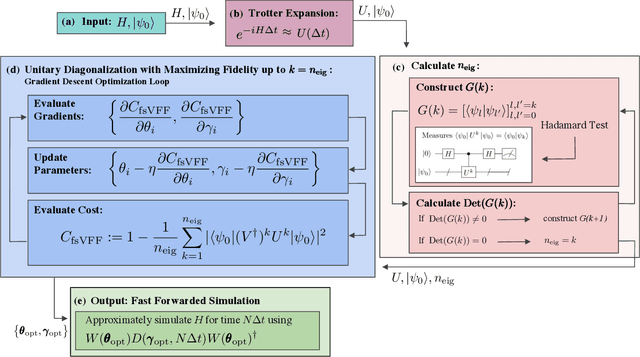
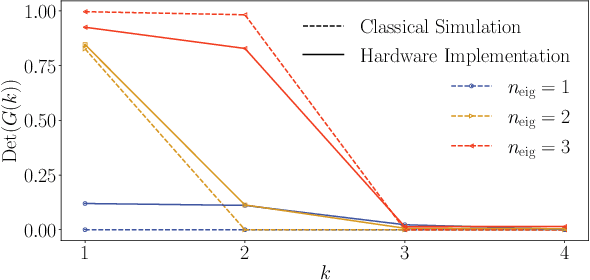
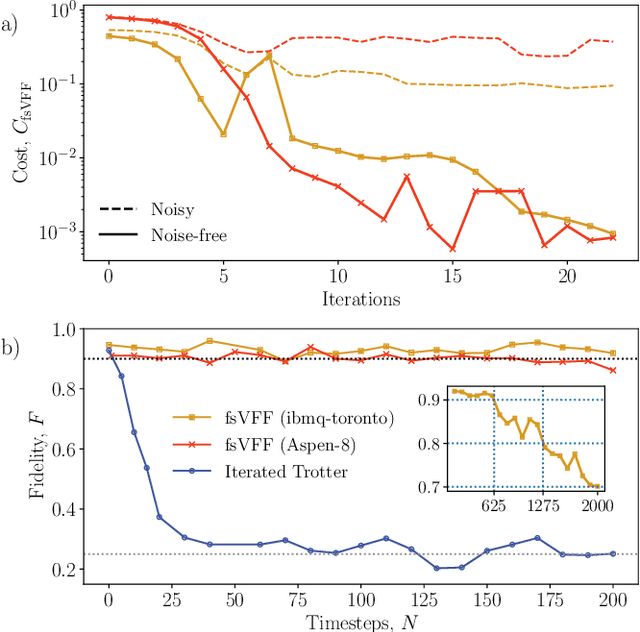
Moderate-size quantum computers are now publicly accessible over the cloud, opening the exciting possibility of performing dynamical simulations of quantum systems. However, while rapidly improving, these devices have short coherence times, limiting the depth of algorithms that may be successfully implemented. Here we demonstrate that, despite these limitations, it is possible to implement long-time, high fidelity simulations on current hardware. Specifically, we simulate an XY-model spin chain on the Rigetti and IBM quantum computers, maintaining a fidelity of at least 0.9 for over 600 time steps. This is a factor of 150 longer than is possible using the iterated Trotter method. Our simulations are performed using a new algorithm that we call the fixed state Variational Fast Forwarding (fsVFF) algorithm. This algorithm decreases the circuit depth and width required for a quantum simulation by finding an approximate diagonalization of a short time evolution unitary. Crucially, fsVFF only requires finding a diagonalization on the subspace spanned by the initial state, rather than on the total Hilbert space as with previous methods, substantially reducing the required resources.