Inference-Based Quantum Sensing

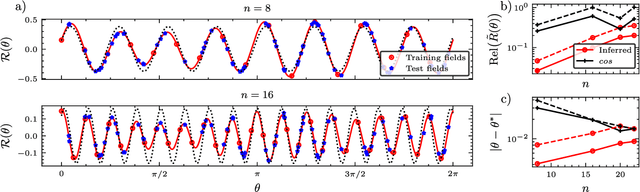
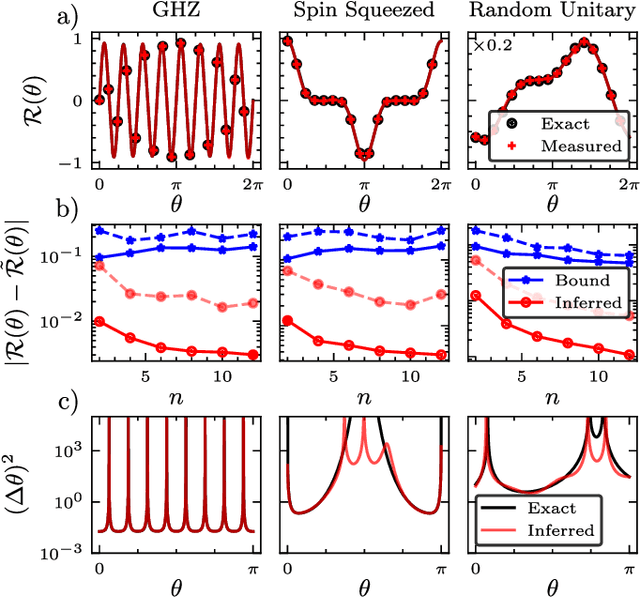
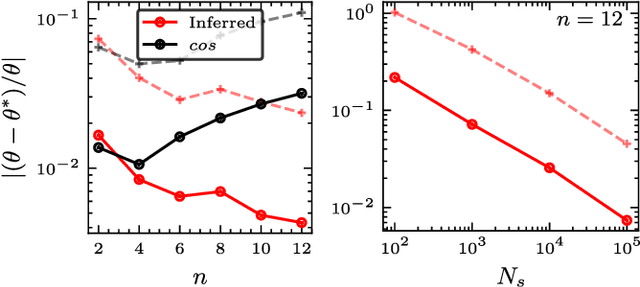
In a standard Quantum Sensing (QS) task one aims at estimating an unknown parameter $\theta$, encoded into an $n$-qubit probe state, via measurements of the system. The success of this task hinges on the ability to correlate changes in the parameter to changes in the system response $\mathcal{R}(\theta)$ (i.e., changes in the measurement outcomes). For simple cases the form of $\mathcal{R}(\theta)$ is known, but the same cannot be said for realistic scenarios, as no general closed-form expression exists. In this work we present an inference-based scheme for QS. We show that, for a general class of unitary families of encoding, $\mathcal{R}(\theta)$ can be fully characterized by only measuring the system response at $2n+1$ parameters. In turn, this allows us to infer the value of an unknown parameter given the measured response, as well as to determine the sensitivity of the sensing scheme, which characterizes its overall performance. We show that inference error is, with high probability, smaller than $\delta$, if one measures the system response with a number of shots that scales only as $\Omega(\log^3(n)/\delta^2)$. Furthermore, the framework presented can be broadly applied as it remains valid for arbitrary probe states and measurement schemes, and, even holds in the presence of quantum noise. We also discuss how to extend our results beyond unitary families. Finally, to showcase our method we implement it for a QS task on real quantum hardware, and in numerical simulations.

Dynamical simulation via quantum machine learning with provable generalization

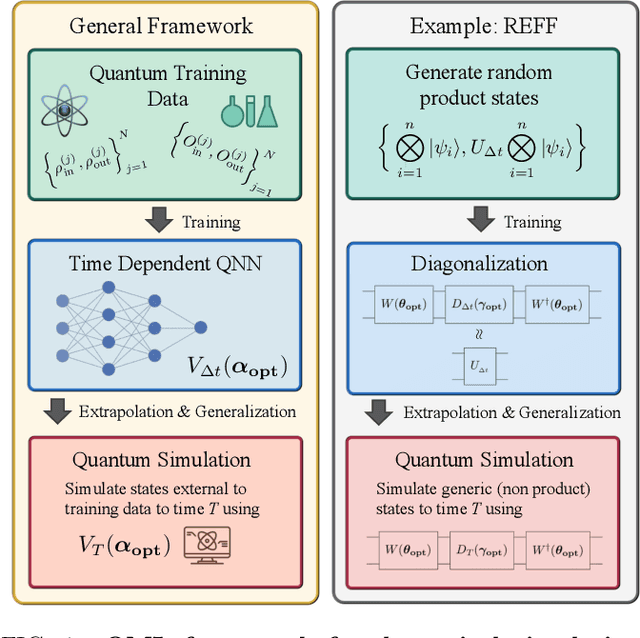
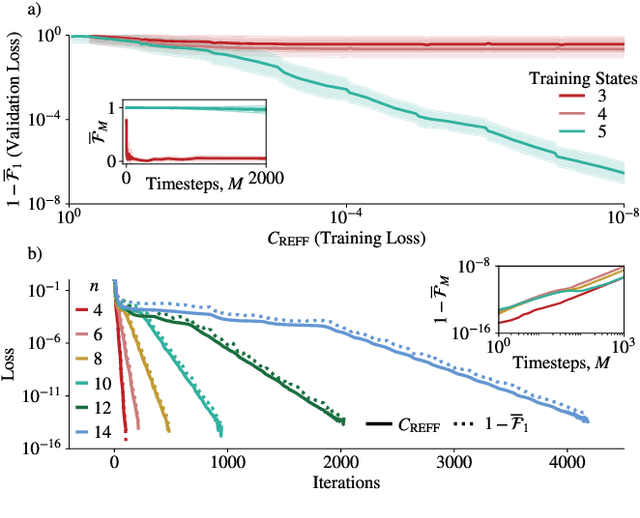
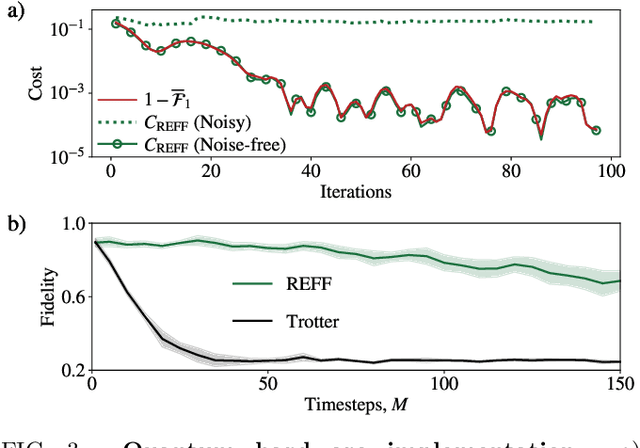
Much attention has been paid to dynamical simulation and quantum machine learning (QML) independently as applications for quantum advantage, while the possibility of using QML to enhance dynamical simulations has not been thoroughly investigated. Here we develop a framework for using QML methods to simulate quantum dynamics on near-term quantum hardware. We use generalization bounds, which bound the error a machine learning model makes on unseen data, to rigorously analyze the training data requirements of an algorithm within this framework. This provides a guarantee that our algorithm is resource-efficient, both in terms of qubit and data requirements. Our numerics exhibit efficient scaling with problem size, and we simulate 20 times longer than Trotterization on IBMQ-Bogota.

Out-of-distribution generalization for learning quantum dynamics

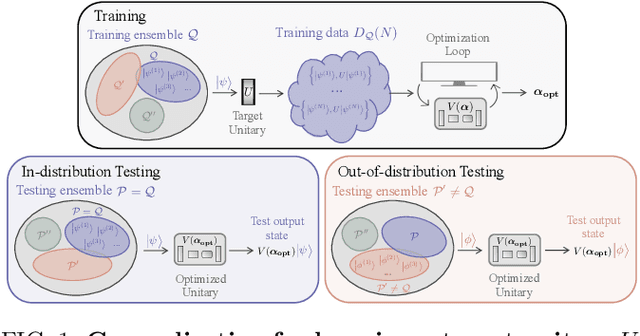
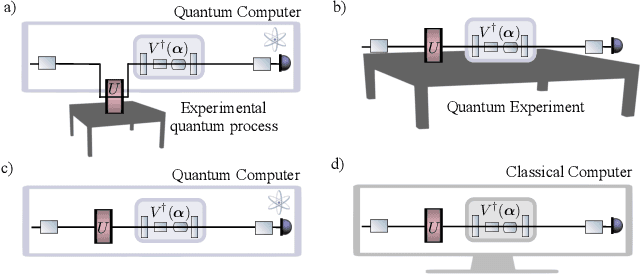
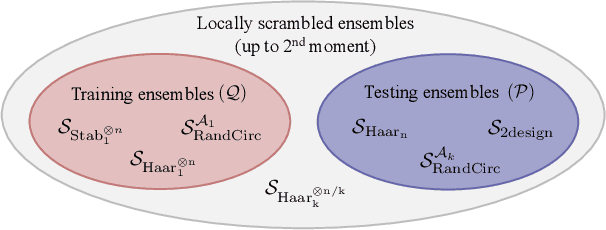
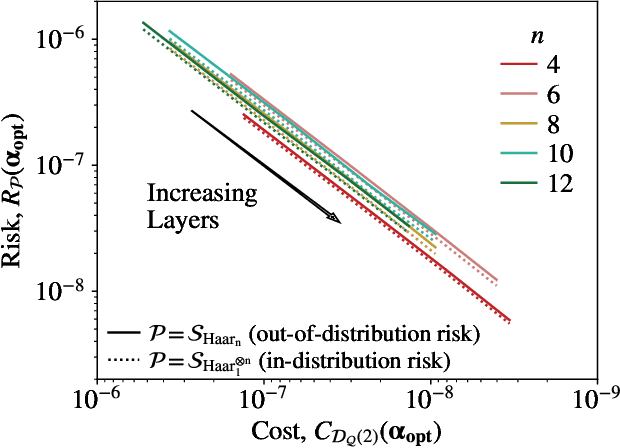
Generalization bounds are a critical tool to assess the training data requirements of Quantum Machine Learning (QML). Recent work has established guarantees for in-distribution generalization of quantum neural networks (QNNs), where training and testing data are assumed to be drawn from the same data distribution. However, there are currently no results on out-of-distribution generalization in QML, where we require a trained model to perform well even on data drawn from a distribution different from the training distribution. In this work, we prove out-of-distribution generalization for the task of learning an unknown unitary using a QNN and for a broad class of training and testing distributions. In particular, we show that one can learn the action of a unitary on entangled states using only product state training data. We numerically illustrate this by showing that the evolution of a Heisenberg spin chain can be learned using only product training states. Since product states can be prepared using only single-qubit gates, this advances the prospects of learning quantum dynamics using near term quantum computers and quantum experiments, and further opens up new methods for both the classical and quantum compilation of quantum circuits.

Absence of Barren Plateaus in Quantum Convolutional Neural Networks

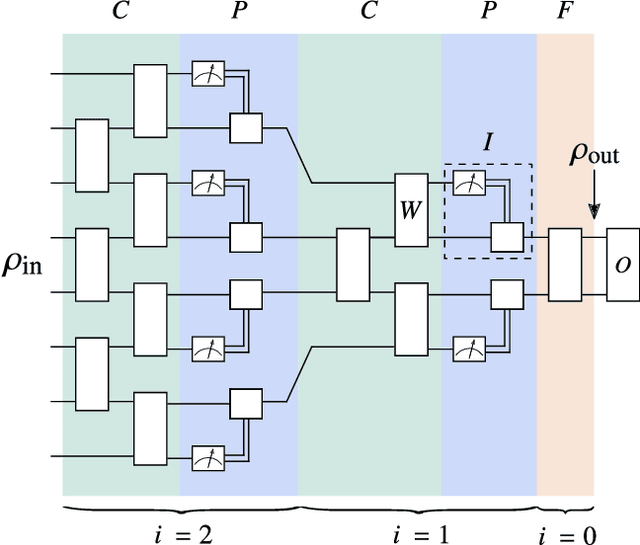
Quantum neural networks (QNNs) have generated excitement around the possibility of efficiently analyzing quantum data. But this excitement has been tempered by the existence of exponentially vanishing gradients, known as barren plateau landscapes, for many QNN architectures. Recently, Quantum Convolutional Neural Networks (QCNNs) have been proposed, involving a sequence of convolutional and pooling layers that reduce the number of qubits while preserving information about relevant data features. In this work we rigorously analyze the gradient scaling for the parameters in the QCNN architecture. We find that the variance of the gradient vanishes no faster than polynomially, implying that QCNNs do not exhibit barren plateaus. This provides an analytical guarantee for the trainability of randomly initialized QCNNs, which singles out QCNNs as being trainable unlike many other QNN architectures. To derive our results we introduce a novel graph-based method to analyze expectation values over Haar-distributed unitaries, which will likely be useful in other contexts. Finally, we perform numerical simulations to verify our analytical results.