The OpenHands Software Agent SDK: A Composable and Extensible Foundation for Production Agents

Agents are now used widely in the process of software development, but building production-ready software engineering agents is a complex task. Deploying software agents effectively requires flexibility in implementation and experimentation, reliable and secure execution, and interfaces for users to interact with agents. In this paper, we present the OpenHands Software Agent SDK, a toolkit for implementing software development agents that satisfy these desiderata. This toolkit is a complete architectural redesign of the agent components of the popular OpenHands framework for software development agents, which has 64k+ GitHub stars. To achieve flexibility, we design a simple interface for implementing agents that requires only a few lines of code in the default case, but is easily extensible to more complex, full-featured agents with features such as custom tools, memory management, and more. For security and reliability, it delivers seamless local-to-remote execution portability, integrated REST/WebSocket services. For interaction with human users, it can connect directly to a variety of interfaces, such as visual workspaces (VS Code, VNC, browser), command-line interfaces, and APIs. Compared with existing SDKs from OpenAI, Claude, and Google, OpenHands uniquely integrates native sandboxed execution, lifecycle control, model-agnostic multi-LLM routing, and built-in security analysis. Empirical results on SWE-Bench Verified and GAIA benchmarks demonstrate strong performance. Put together, these elements allow the OpenHands Software Agent SDK to provide a practical foundation for prototyping, unlocking new classes of custom applications, and reliably deploying agents at scale.

Agricultural Landscape Understanding At Country-Scale

Agricultural landscapes are quite complex, especially in the Global South where fields are smaller, and agricultural practices are more varied. In this paper we report on our progress in digitizing the agricultural landscape (natural and man-made) in our study region of India. We use high resolution imagery and a UNet style segmentation model to generate the first of its kind national-scale multi-class panoptic segmentation output. Through this work we have been able to identify individual fields across 151.7M hectares, and delineating key features such as water resources and vegetation. We share how this output was validated by our team and externally by downstream users, including some sample use cases that can lead to targeted data driven decision making. We believe this dataset will contribute towards digitizing agriculture by generating the foundational baselayer.

Empirical Tests of Optimization Assumptions in Deep Learning

There is a significant gap between our theoretical understanding of optimization algorithms used in deep learning and their practical performance. Theoretical development usually focuses on proving convergence guarantees under a variety of different assumptions, which are themselves often chosen based on a rough combination of intuitive match to practice and analytical convenience. The theory/practice gap may then arise because of the failure to prove a theorem under such assumptions, or because the assumptions do not reflect reality. In this paper, we carefully measure the degree to which these assumptions are capable of explaining modern optimization algorithms by developing new empirical metrics that closely track the key quantities that must be controlled in theoretical analysis. All of our tested assumptions (including typical modern assumptions based on bounds on the Hessian) fail to reliably capture optimization performance. This highlights a need for new empirical verification of analytical assumptions used in theoretical analysis.

Private Zeroth-Order Nonsmooth Nonconvex Optimization

We introduce a new zeroth-order algorithm for private stochastic optimization on nonconvex and nonsmooth objectives. Given a dataset of size $M$, our algorithm ensures $(\alpha,\alpha\rho^2/2)$-R\'enyi differential privacy and finds a $(\delta,\epsilon)$-stationary point so long as $M=\tilde\Omega\left(\frac{d}{\delta\epsilon^3} + \frac{d^{3/2}}{\rho\delta\epsilon^2}\right)$. This matches the optimal complexity of its non-private zeroth-order analog. Notably, although the objective is not smooth, we have privacy ``for free'' whenever $\rho \ge \sqrt{d}\epsilon$.

Orthogonally weighted $\ell_{2,1}$ regularization for rank-aware joint sparse recovery: algorithm and analysis

We propose and analyze an efficient algorithm for solving the joint sparse recovery problem using a new regularization-based method, named orthogonally weighted $\ell_{2,1}$ ($\mathit{ow}\ell_{2,1}$), which is specifically designed to take into account the rank of the solution matrix. This method has applications in feature extraction, matrix column selection, and dictionary learning, and it is distinct from commonly used $\ell_{2,1}$ regularization and other existing regularization-based approaches because it can exploit the full rank of the row-sparse solution matrix, a key feature in many applications. We provide a proof of the method's rank-awareness, establish the existence of solutions to the proposed optimization problem, and develop an efficient algorithm for solving it, whose convergence is analyzed. We also present numerical experiments to illustrate the theory and demonstrate the effectiveness of our method on real-life problems.

Point Cloud Data Simulation and Modelling with Aize Workspace

This work takes a look at data models often used in digital twins and presents preliminary results specifically from surface reconstruction and semantic segmentation models trained using simulated data. This work is expected to serve as a ground work for future endeavours in data contextualisation inside a digital twin.

Momentum Aggregation for Private Non-convex ERM

We introduce new algorithms and convergence guarantees for privacy-preserving non-convex Empirical Risk Minimization (ERM) on smooth $d$-dimensional objectives. We develop an improved sensitivity analysis of stochastic gradient descent on smooth objectives that exploits the recurrence of examples in different epochs. By combining this new approach with recent analysis of momentum with private aggregation techniques, we provide an $(\epsilon,\delta)$-differential private algorithm that finds a gradient of norm $\tilde O\left(\frac{d^{1/3}}{(\epsilon N)^{2/3}}\right)$ in $O\left(\frac{N^{7/3}\epsilon^{4/3}}{d^{2/3}}\right)$ gradient evaluations, improving the previous best gradient bound of $\tilde O\left(\frac{d^{1/4}}{\sqrt{\epsilon N}}\right)$.

Differentially Private Online-to-Batch for Smooth Losses

We develop a new reduction that converts any online convex optimization algorithm suffering $O(\sqrt{T})$ regret into an $\epsilon$-differentially private stochastic convex optimization algorithm with the optimal convergence rate $\tilde O(1/\sqrt{T} + \sqrt{d}/\epsilon T)$ on smooth losses in linear time, forming a direct analogy to the classical non-private "online-to-batch" conversion. By applying our techniques to more advanced adaptive online algorithms, we produce adaptive differentially private counterparts whose convergence rates depend on apriori unknown variances or parameter norms.

Model Calibration of the Liquid Mercury Spallation Target using Evolutionary Neural Networks and Sparse Polynomial Expansions

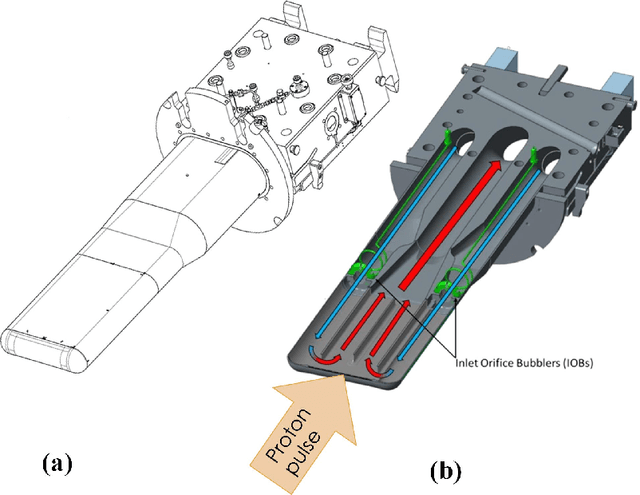
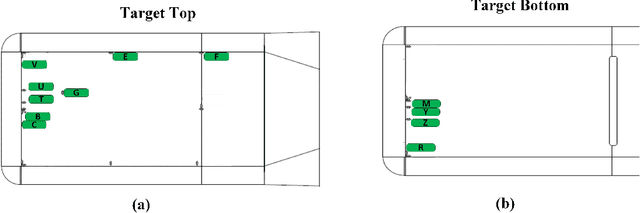
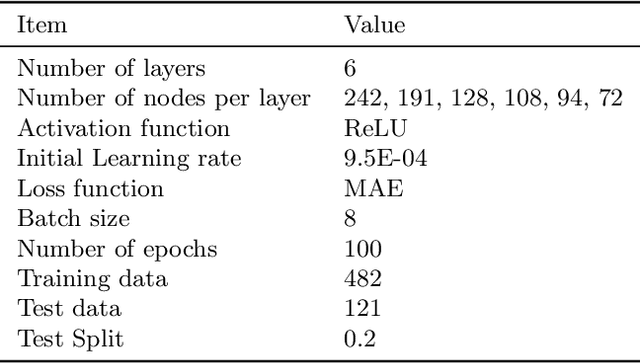
The mercury constitutive model predicting the strain and stress in the target vessel plays a central role in improving the lifetime prediction and future target designs of the mercury targets at the Spallation Neutron Source (SNS). We leverage the experiment strain data collected over multiple years to improve the mercury constitutive model through a combination of large-scale simulations of the target behavior and the use of machine learning tools for parameter estimation. We present two interdisciplinary approaches for surrogate-based model calibration of expensive simulations using evolutionary neural networks and sparse polynomial expansions. The experiments and results of the two methods show a very good agreement for the solid mechanics simulation of the mercury spallation target. The proposed methods are used to calibrate the tensile cutoff threshold, mercury density, and mercury speed of sound during intense proton pulse experiments. Using strain experimental data from the mercury target sensors, the newly calibrated simulations achieve 7\% average improvement on the signal prediction accuracy and 8\% reduction in mean absolute error compared to previously reported reference parameters, with some sensors experiencing up to 30\% improvement. The proposed calibrated simulations can significantly aid in fatigue analysis to estimate the mercury target lifetime and integrity, which reduces abrupt target failure and saves a tremendous amount of costs. However, an important conclusion from this work points out to a deficiency in the current constitutive model based on the equation of state in capturing the full physics of the spallation reaction. Given that some of the calibrated parameters that show a good agreement with the experimental data can be nonphysical mercury properties, we need a more advanced two-phase flow model to capture bubble dynamics and mercury cavitation.

Correcting Momentum with Second-order Information

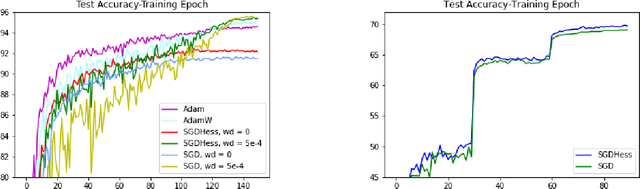
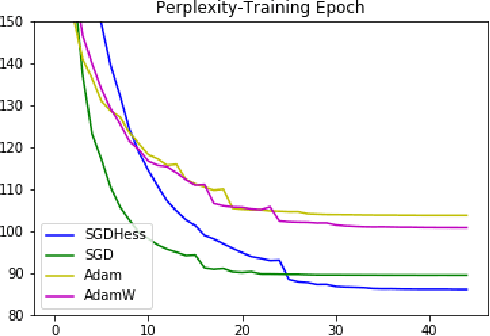
We develop a new algorithm for non-convex stochastic optimization that finds an $\epsilon$-critical point in the optimal $O(\epsilon^{-3})$ stochastic gradient and hessian-vector product computations. Our algorithm uses Hessian-vector products to "correct" a bias term in the momentum of SGD with momentum. This leads to better gradient estimates in a manner analogous to variance reduction methods. In contrast to prior work, we do not require excessively large batch sizes (or indeed any restrictions at all on the batch size), and both our algorithm and its analysis are much simpler. We validate our results on a variety of large-scale deep learning benchmarks and architectures, where we see improvements over SGD and Adam.