Solving Nonlinear PDEs with Sparse Radial Basis Function Networks

We propose a novel framework for solving nonlinear PDEs using sparse radial basis function (RBF) networks. Sparsity-promoting regularization is employed to prevent over-parameterization and reduce redundant features. This work is motivated by longstanding challenges in traditional RBF collocation methods, along with the limitations of physics-informed neural networks (PINNs) and Gaussian process (GP) approaches, aiming to blend their respective strengths in a unified framework. The theoretical foundation of our approach lies in the function space of Reproducing Kernel Banach Spaces (RKBS) induced by one-hidden-layer neural networks of possibly infinite width. We prove a representer theorem showing that the solution to the sparse optimization problem in the RKBS admits a finite solution and establishes error bounds that offer a foundation for generalizing classical numerical analysis. The algorithmic framework is based on a three-phase algorithm to maintain computational efficiency through adaptive feature selection, second-order optimization, and pruning of inactive neurons. Numerical experiments demonstrate the effectiveness of our method and highlight cases where it offers notable advantages over GP approaches. This work opens new directions for adaptive PDE solvers grounded in rigorous analysis with efficient, learning-inspired implementation.

Nonuniform random feature models using derivative information

We propose nonuniform data-driven parameter distributions for neural network initialization based on derivative data of the function to be approximated. These parameter distributions are developed in the context of non-parametric regression models based on shallow neural networks, and compare favorably to well-established uniform random feature models based on conventional weight initialization. We address the cases of Heaviside and ReLU activation functions, and their smooth approximations (sigmoid and softplus), and use recent results on the harmonic analysis and sparse representation of neural networks resulting from fully trained optimal networks. Extending analytic results that give exact representation, we obtain densities that concentrate in regions of the parameter space corresponding to neurons that are well suited to model the local derivatives of the unknown function. Based on these results, we suggest simplifications of these exact densities based on approximate derivative data in the input points that allow for very efficient sampling and lead to performance of random feature models close to optimal networks in several scenarios.

Orthogonally weighted $\ell_{2,1}$ regularization for rank-aware joint sparse recovery: algorithm and analysis

We propose and analyze an efficient algorithm for solving the joint sparse recovery problem using a new regularization-based method, named orthogonally weighted $\ell_{2,1}$ ($\mathit{ow}\ell_{2,1}$), which is specifically designed to take into account the rank of the solution matrix. This method has applications in feature extraction, matrix column selection, and dictionary learning, and it is distinct from commonly used $\ell_{2,1}$ regularization and other existing regularization-based approaches because it can exploit the full rank of the row-sparse solution matrix, a key feature in many applications. We provide a proof of the method's rank-awareness, establish the existence of solutions to the proposed optimization problem, and develop an efficient algorithm for solving it, whose convergence is analyzed. We also present numerical experiments to illustrate the theory and demonstrate the effectiveness of our method on real-life problems.

Nonconvex penalization for sparse neural networks

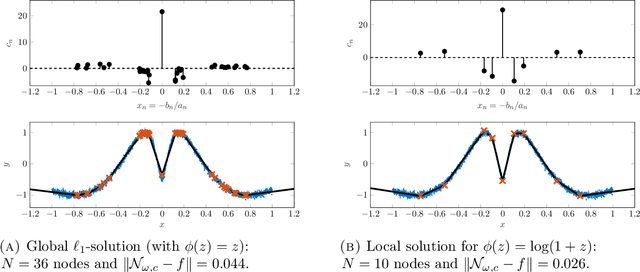
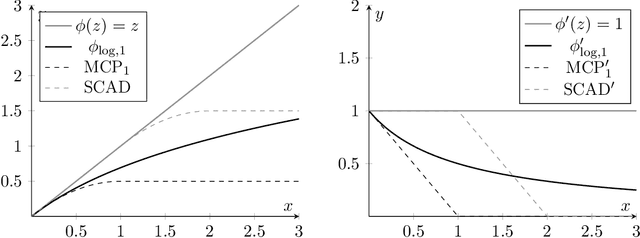
Training methods for artificial neural networks often rely on over-parameterization and random initialization in order to avoid spurious local minima of the loss function that fail to fit the data properly. To sidestep this, one can employ convex neural networks, which combine a convex interpretation of the loss term, sparsity promoting penalization of the outer weights, and greedy neuron insertion. However, the canonical $\ell_1$ penalty does not achieve a sufficient reduction in the number of nodes in a shallow network in the presence of large amounts of data, as observed in practice and supported by our theory. As a remedy, we propose a nonconvex penalization method for the outer weights that maintains the advantages of the convex approach. We investigate the analytic aspects of the method in the context of neural network integral representations and prove attainability of minimizers, together with a finite support property and approximation guarantees. Additionally, we describe how to numerically solve the minimization problem with an adaptive algorithm combining local gradient based training, and adaptive node insertion and extraction.