Score-based Continuous-time Discrete Diffusion Models

Score-based modeling through stochastic differential equations (SDEs) has provided a new perspective on diffusion models, and demonstrated superior performance on continuous data. However, the gradient of the log-likelihood function, i.e., the score function, is not properly defined for discrete spaces. This makes it non-trivial to adapt \textcolor{\cdiff}{the score-based modeling} to categorical data. In this paper, we extend diffusion models to discrete variables by introducing a stochastic jump process where the reverse process denoises via a continuous-time Markov chain. This formulation admits an analytical simulation during backward sampling. To learn the reverse process, we extend score matching to general categorical data and show that an unbiased estimator can be obtained via simple matching of the conditional marginal distributions. We demonstrate the effectiveness of the proposed method on a set of synthetic and real-world music and image benchmarks.

Learning to Optimize with Stochastic Dominance Constraints

In real-world decision-making, uncertainty is important yet difficult to handle. Stochastic dominance provides a theoretically sound approach for comparing uncertain quantities, but optimization with stochastic dominance constraints is often computationally expensive, which limits practical applicability. In this paper, we develop a simple yet efficient approach for the problem, the Light Stochastic Dominance Solver (light-SD), that leverages useful properties of the Lagrangian. We recast the inner optimization in the Lagrangian as a learning problem for surrogate approximation, which bypasses apparent intractability and leads to tractable updates or even closed-form solutions for gradient calculations. We prove convergence of the algorithm and test it empirically. The proposed light-SD demonstrates superior performance on several representative problems ranging from finance to supply chain management.

Optimal Scaling for Locally Balanced Proposals in Discrete Spaces

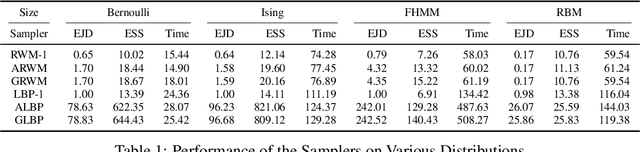
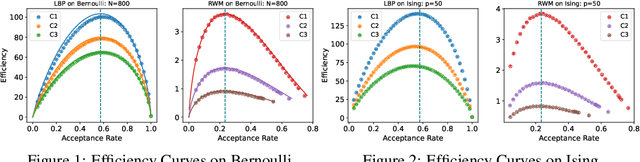
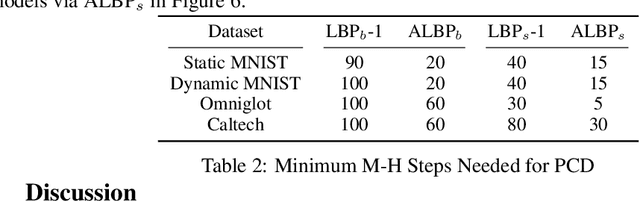
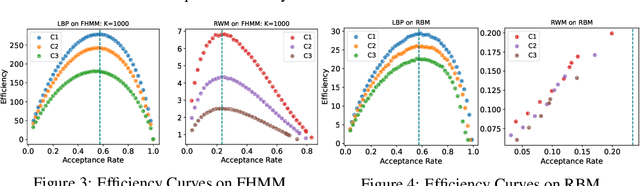
Optimal scaling has been well studied for Metropolis-Hastings (M-H) algorithms in continuous spaces, but a similar understanding has been lacking in discrete spaces. Recently, a family of locally balanced proposals (LBP) for discrete spaces has been proved to be asymptotically optimal, but the question of optimal scaling has remained open. In this paper, we establish, for the first time, that the efficiency of M-H in discrete spaces can also be characterized by an asymptotic acceptance rate that is independent of the target distribution. Moreover, we verify, both theoretically and empirically, that the optimal acceptance rates for LBP and random walk Metropolis (RWM) are $0.574$ and $0.234$ respectively. These results also help establish that LBP is asymptotically $O(N^\frac{2}{3})$ more efficient than RWM with respect to model dimension $N$. Knowledge of the optimal acceptance rate allows one to automatically tune the neighborhood size of a proposal distribution in a discrete space, directly analogous to step-size control in continuous spaces. We demonstrate empirically that such adaptive M-H sampling can robustly improve sampling in a variety of target distributions in discrete spaces, including training deep energy based models.

Annealed Training for Combinatorial Optimization on Graphs

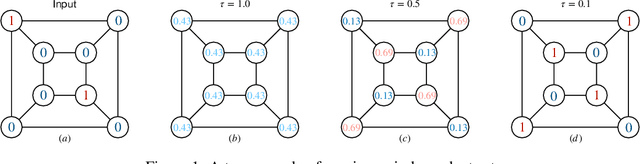
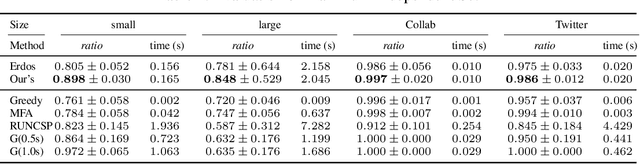
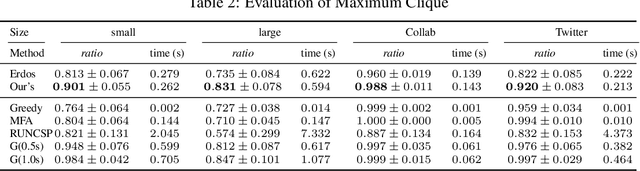
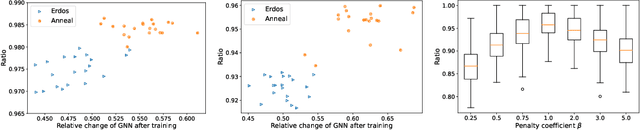
The hardness of combinatorial optimization (CO) problems hinders collecting solutions for supervised learning. However, learning neural networks for CO problems is notoriously difficult in lack of the labeled data as the training is easily trapped at local optima. In this work, we propose a simple but effective annealed training framework for CO problems. In particular, we transform CO problems into unbiased energy-based models (EBMs). We carefully selected the penalties terms so as to make the EBMs as smooth as possible. Then we train graph neural networks to approximate the EBMs. To prevent the training from being stuck at local optima near the initialization, we introduce an annealed loss function. An experimental evaluation demonstrates that our annealed training framework obtains substantial improvements. In four types of CO problems, our method achieves performance substantially better than other unsupervised neural methods on both synthetic and real-world graphs.

Discrete Langevin Sampler via Wasserstein Gradient Flow

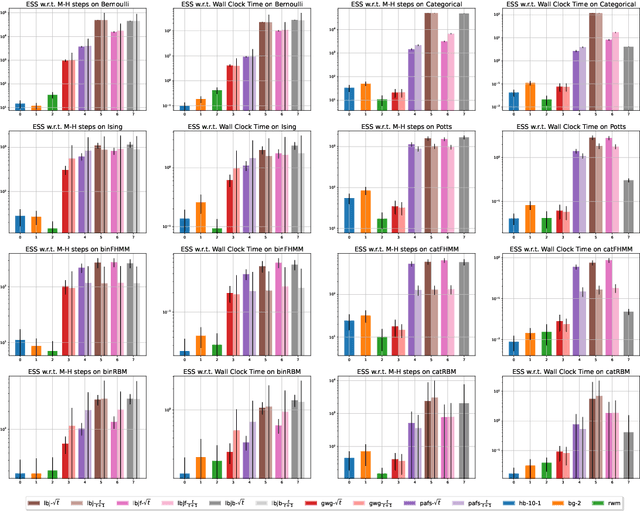
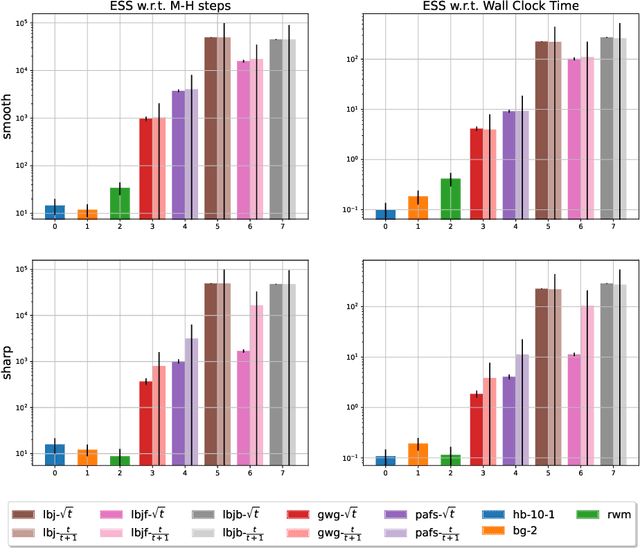
Recently, a family of locally balanced (LB) samplers has demonstrated excellent performance at sampling and learning energy-based models (EBMs) in discrete spaces. However, the theoretical understanding of this success is limited. In this work, we show how LB functions give rise to LB dynamics corresponding to Wasserstein gradient flow in a discrete space. From first principles, previous LB samplers can then be seen as discretizations of the LB dynamics with respect to Hamming distance. Based on this observation, we propose a new algorithm, the Locally Balanced Jump (LBJ), by discretizing the LB dynamics with respect to simulation time. As a result, LBJ has a location-dependent "velocity" that allows it to make proposals with larger distances. Additionally, LBJ decouples each dimension into independent sub-processes, enabling convenient parallel implementation. We demonstrate the advantages of LBJ for sampling and learning in various binary and categorical distributions.

CrossBeam: Learning to Search in Bottom-Up Program Synthesis

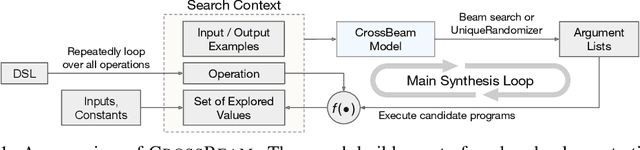
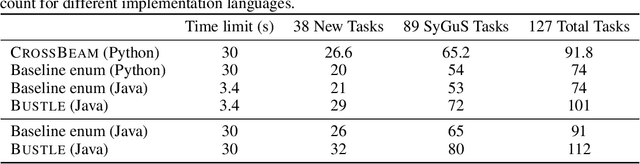
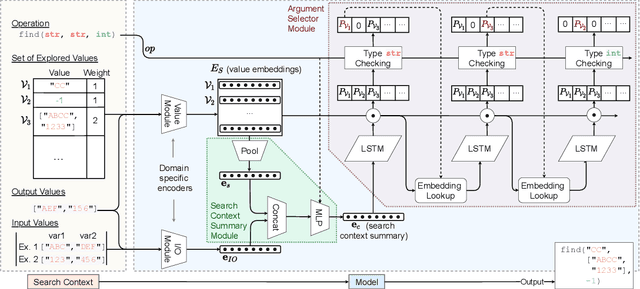
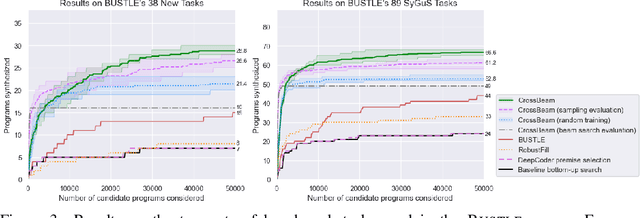
Many approaches to program synthesis perform a search within an enormous space of programs to find one that satisfies a given specification. Prior works have used neural models to guide combinatorial search algorithms, but such approaches still explore a huge portion of the search space and quickly become intractable as the size of the desired program increases. To tame the search space blowup, we propose training a neural model to learn a hands-on search policy for bottom-up synthesis, instead of relying on a combinatorial search algorithm. Our approach, called CrossBeam, uses the neural model to choose how to combine previously-explored programs into new programs, taking into account the search history and partial program executions. Motivated by work in structured prediction on learning to search, CrossBeam is trained on-policy using data extracted from its own bottom-up searches on training tasks. We evaluate CrossBeam in two very different domains, string manipulation and logic programming. We observe that CrossBeam learns to search efficiently, exploring much smaller portions of the program space compared to the state-of-the-art.

Neural Stochastic Dual Dynamic Programming

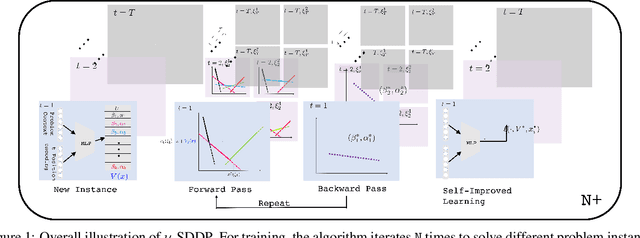
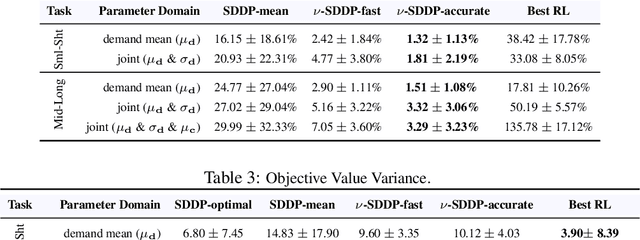
Stochastic dual dynamic programming (SDDP) is a state-of-the-art method for solving multi-stage stochastic optimization, widely used for modeling real-world process optimization tasks. Unfortunately, SDDP has a worst-case complexity that scales exponentially in the number of decision variables, which severely limits applicability to only low dimensional problems. To overcome this limitation, we extend SDDP by introducing a trainable neural model that learns to map problem instances to a piece-wise linear value function within intrinsic low-dimension space, which is architected specifically to interact with a base SDDP solver, so that can accelerate optimization performance on new instances. The proposed Neural Stochastic Dual Dynamic Programming ($\nu$-SDDP) continually self-improves by solving successive problems. An empirical investigation demonstrates that $\nu$-SDDP can significantly reduce problem solving cost without sacrificing solution quality over competitors such as SDDP and reinforcement learning algorithms, across a range of synthetic and real-world process optimization problems.

SMORE: Knowledge Graph Completion and Multi-hop Reasoning in Massive Knowledge Graphs

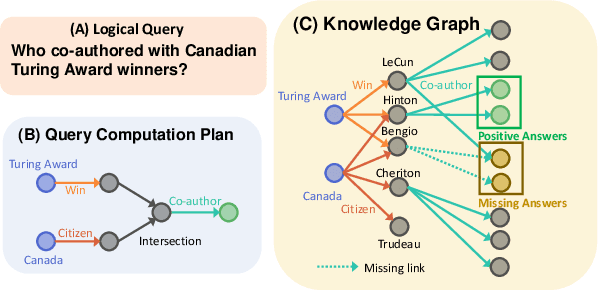
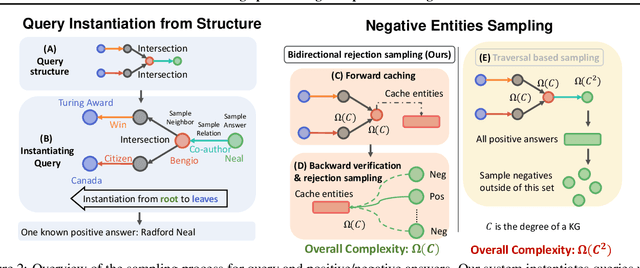
Knowledge graphs (KGs) capture knowledge in the form of head--relation--tail triples and are a crucial component in many AI systems. There are two important reasoning tasks on KGs: (1) single-hop knowledge graph completion, which involves predicting individual links in the KG; and (2), multi-hop reasoning, where the goal is to predict which KG entities satisfy a given logical query. Embedding-based methods solve both tasks by first computing an embedding for each entity and relation, then using them to form predictions. However, existing scalable KG embedding frameworks only support single-hop knowledge graph completion and cannot be applied to the more challenging multi-hop reasoning task. Here we present Scalable Multi-hOp REasoning (SMORE), the first general framework for both single-hop and multi-hop reasoning in KGs. Using a single machine SMORE can perform multi-hop reasoning in Freebase KG (86M entities, 338M edges), which is 1,500x larger than previously considered KGs. The key to SMORE's runtime performance is a novel bidirectional rejection sampling that achieves a square root reduction of the complexity of online training data generation. Furthermore, SMORE exploits asynchronous scheduling, overlapping CPU-based data sampling, GPU-based embedding computation, and frequent CPU--GPU IO. SMORE increases throughput (i.e., training speed) over prior multi-hop KG frameworks by 2.2x with minimal GPU memory requirements (2GB for training 400-dim embeddings on 86M-node Freebase) and achieves near linear speed-up with the number of GPUs. Moreover, on the simpler single-hop knowledge graph completion task SMORE achieves comparable or even better runtime performance to state-of-the-art frameworks on both single GPU and multi-GPU settings.

Combiner: Full Attention Transformer with Sparse Computation Cost

Transformers provide a class of expressive architectures that are extremely effective for sequence modeling. However, the key limitation of transformers is their quadratic memory and time complexity $\mathcal{O}(L^2)$ with respect to the sequence length in attention layers, which restricts application in extremely long sequences. Most existing approaches leverage sparsity or low-rank assumptions in the attention matrix to reduce cost, but sacrifice expressiveness. Instead, we propose Combiner, which provides full attention capability in each attention head while maintaining low computation and memory complexity. The key idea is to treat the self-attention mechanism as a conditional expectation over embeddings at each location, and approximate the conditional distribution with a structured factorization. Each location can attend to all other locations, either via direct attention, or through indirect attention to abstractions, which are again conditional expectations of embeddings from corresponding local regions. We show that most sparse attention patterns used in existing sparse transformers are able to inspire the design of such factorization for full attention, resulting in the same sub-quadratic cost ($\mathcal{O}(L\log(L))$ or $\mathcal{O}(L\sqrt{L})$). Combiner is a drop-in replacement for attention layers in existing transformers and can be easily implemented in common frameworks. An experimental evaluation on both autoregressive and bidirectional sequence tasks demonstrates the effectiveness of this approach, yielding state-of-the-art results on several image and text modeling tasks.

SpreadsheetCoder: Formula Prediction from Semi-structured Context

Spreadsheet formula prediction has been an important program synthesis problem with many real-world applications. Previous works typically utilize input-output examples as the specification for spreadsheet formula synthesis, where each input-output pair simulates a separate row in the spreadsheet. However, this formulation does not fully capture the rich context in real-world spreadsheets. First, spreadsheet data entries are organized as tables, thus rows and columns are not necessarily independent from each other. In addition, many spreadsheet tables include headers, which provide high-level descriptions of the cell data. However, previous synthesis approaches do not consider headers as part of the specification. In this work, we present the first approach for synthesizing spreadsheet formulas from tabular context, which includes both headers and semi-structured tabular data. In particular, we propose SpreadsheetCoder, a BERT-based model architecture to represent the tabular context in both row-based and column-based formats. We train our model on a large dataset of spreadsheets, and demonstrate that SpreadsheetCoder achieves top-1 prediction accuracy of 42.51%, which is a considerable improvement over baselines that do not employ rich tabular context. Compared to the rule-based system, SpreadsheetCoder assists 82% more users in composing formulas on Google Sheets.