Data Augmentations in Deep Weight Spaces

Learning in weight spaces, where neural networks process the weights of other deep neural networks, has emerged as a promising research direction with applications in various fields, from analyzing and editing neural fields and implicit neural representations, to network pruning and quantization. Recent works designed architectures for effective learning in that space, which takes into account its unique, permutation-equivariant, structure. Unfortunately, so far these architectures suffer from severe overfitting and were shown to benefit from large datasets. This poses a significant challenge because generating data for this learning setup is laborious and time-consuming since each data sample is a full set of network weights that has to be trained. In this paper, we address this difficulty by investigating data augmentations for weight spaces, a set of techniques that enable generating new data examples on the fly without having to train additional input weight space elements. We first review several recently proposed data augmentation schemes %that were proposed recently and divide them into categories. We then introduce a novel augmentation scheme based on the Mixup method. We evaluate the performance of these techniques on existing benchmarks as well as new benchmarks we generate, which can be valuable for future studies.

Efficient Subgraph GNNs by Learning Effective Selection Policies

Subgraph GNNs are provably expressive neural architectures that learn graph representations from sets of subgraphs. Unfortunately, their applicability is hampered by the computational complexity associated with performing message passing on many subgraphs. In this paper, we consider the problem of learning to select a small subset of the large set of possible subgraphs in a data-driven fashion. We first motivate the problem by proving that there are families of WL-indistinguishable graphs for which there exist efficient subgraph selection policies: small subsets of subgraphs that can already identify all the graphs within the family. We then propose a new approach, called Policy-Learn, that learns how to select subgraphs in an iterative manner. We prove that, unlike popular random policies and prior work addressing the same problem, our architecture is able to learn the efficient policies mentioned above. Our experimental results demonstrate that Policy-Learn outperforms existing baselines across a wide range of datasets.

Equivariant Deep Weight Space Alignment

Permutation symmetries of deep networks make simple operations like model averaging and similarity estimation challenging. In many cases, aligning the weights of the networks, i.e., finding optimal permutations between their weights, is necessary. More generally, weight alignment is essential for a wide range of applications, from model merging, through exploring the optimization landscape of deep neural networks, to defining meaningful distance functions between neural networks. Unfortunately, weight alignment is an NP-hard problem. Prior research has mainly focused on solving relaxed versions of the alignment problem, leading to either time-consuming methods or sub-optimal solutions. To accelerate the alignment process and improve its quality, we propose a novel framework aimed at learning to solve the weight alignment problem, which we name Deep-Align. To that end, we first demonstrate that weight alignment adheres to two fundamental symmetries and then, propose a deep architecture that respects these symmetries. Notably, our framework does not require any labeled data. We provide a theoretical analysis of our approach and evaluate Deep-Align on several types of network architectures and learning setups. Our experimental results indicate that a feed-forward pass with Deep-Align produces better or equivalent alignments compared to those produced by current optimization algorithms. Additionally, our alignments can be used as an initialization for other methods to gain even better solutions with a significant speedup in convergence.

Norm-guided latent space exploration for text-to-image generation

Text-to-image diffusion models show great potential in synthesizing a large variety of concepts in new compositions and scenarios. However, their latent seed space is still not well understood and has been shown to have an impact in generating new and rare concepts. Specifically, simple operations like interpolation and centroid finding work poorly with the standard Euclidean and spherical metrics in the latent space. This paper makes the observation that current training procedures make diffusion models biased toward inputs with a narrow range of norm values. This has strong implications for methods that rely on seed manipulation for image generation that can be further applied to few-shot and long-tail learning tasks. To address this issue, we propose a novel method for interpolating between two seeds and demonstrate that it defines a new non-Euclidean metric that takes into account a norm-based prior on seeds. We describe a simple yet efficient algorithm for approximating this metric and use it to further define centroids in the latent seed space. We show that our new interpolation and centroid evaluation techniques significantly enhance the generation of rare concept images. This further leads to state-of-the-art performance on few-shot and long-tail benchmarks, improving prior approach in terms of generation speed, image quality, and semantic content.

Hierarchical Graph Neural Network with Cross-Attention for Cross-Device User Matching

Cross-device user matching is a critical problem in numerous domains, including advertising, recommender systems, and cybersecurity. It involves identifying and linking different devices belonging to the same person, utilizing sequence logs. Previous data mining techniques have struggled to address the long-range dependencies and higher-order connections between the logs. Recently, researchers have modeled this problem as a graph problem and proposed a two-tier graph contextual embedding (TGCE) neural network architecture, which outperforms previous methods. In this paper, we propose a novel hierarchical graph neural network architecture (HGNN), which has a more computationally efficient second level design than TGCE. Furthermore, we introduce a cross-attention (Cross-Att) mechanism in our model, which improves performance by 5% compared to the state-of-the-art TGCE method.

Graph Positional Encoding via Random Feature Propagation

Two main families of node feature augmentation schemes have been explored for enhancing GNNs: random features and spectral positional encoding. Surprisingly, however, there is still no clear understanding of the relation between these two augmentation schemes. Here we propose a novel family of positional encoding schemes which draws a link between the above two approaches and improves over both. The new approach, named Random Feature Propagation (RFP), is inspired by the power iteration method and its generalizations. It concatenates several intermediate steps of an iterative algorithm for computing the dominant eigenvectors of a propagation matrix, starting from random node features. Notably, these propagation steps are based on graph-dependent propagation operators that can be either predefined or learned. We explore the theoretical and empirical benefits of RFP. First, we provide theoretical justifications for using random features, for incorporating early propagation steps, and for using multiple random initializations. Then, we empirically demonstrate that RFP significantly outperforms both spectral PE and random features in multiple node classification and graph classification benchmarks.

Equivariant Polynomials for Graph Neural Networks

Graph Neural Networks (GNN) are inherently limited in their expressive power. Recent seminal works (Xu et al., 2019; Morris et al., 2019b) introduced the Weisfeiler-Lehman (WL) hierarchy as a measure of expressive power. Although this hierarchy has propelled significant advances in GNN analysis and architecture developments, it suffers from several significant limitations. These include a complex definition that lacks direct guidance for model improvement and a WL hierarchy that is too coarse to study current GNNs. This paper introduces an alternative expressive power hierarchy based on the ability of GNNs to calculate equivariant polynomials of a certain degree. As a first step, we provide a full characterization of all equivariant graph polynomials by introducing a concrete basis, significantly generalizing previous results. Each basis element corresponds to a specific multi-graph, and its computation over some graph data input corresponds to a tensor contraction problem. Second, we propose algorithmic tools for evaluating the expressiveness of GNNs using tensor contraction sequences, and calculate the expressive power of popular GNNs. Finally, we enhance the expressivity of common GNN architectures by adding polynomial features or additional operations / aggregations inspired by our theory. These enhanced GNNs demonstrate state-of-the-art results in experiments across multiple graph learning benchmarks.

Equivariant Architectures for Learning in Deep Weight Spaces

Designing machine learning architectures for processing neural networks in their raw weight matrix form is a newly introduced research direction. Unfortunately, the unique symmetry structure of deep weight spaces makes this design very challenging. If successful, such architectures would be capable of performing a wide range of intriguing tasks, from adapting a pre-trained network to a new domain to editing objects represented as functions (INRs or NeRFs). As a first step towards this goal, we present here a novel network architecture for learning in deep weight spaces. It takes as input a concatenation of weights and biases of a pre-trained MLP and processes it using a composition of layers that are equivariant to the natural permutation symmetry of the MLP's weights: Changing the order of neurons in intermediate layers of the MLP does not affect the function it represents. We provide a full characterization of all affine equivariant and invariant layers for these symmetries and show how these layers can be implemented using three basic operations: pooling, broadcasting, and fully connected layers applied to the input in an appropriate manner. We demonstrate the effectiveness of our architecture and its advantages over natural baselines in a variety of learning tasks.

Generalized Laplacian Positional Encoding for Graph Representation Learning

Graph neural networks (GNNs) are the primary tool for processing graph-structured data. Unfortunately, the most commonly used GNNs, called Message Passing Neural Networks (MPNNs) suffer from several fundamental limitations. To overcome these limitations, recent works have adapted the idea of positional encodings to graph data. This paper draws inspiration from the recent success of Laplacian-based positional encoding and defines a novel family of positional encoding schemes for graphs. We accomplish this by generalizing the optimization problem that defines the Laplace embedding to more general dissimilarity functions rather than the 2-norm used in the original formulation. This family of positional encodings is then instantiated by considering p-norms. We discuss a method for calculating these positional encoding schemes, implement it in PyTorch and demonstrate how the resulting positional encoding captures different properties of the graph. Furthermore, we demonstrate that this novel family of positional encodings can improve the expressive power of MPNNs. Lastly, we present preliminary experimental results.

Understanding and Extending Subgraph GNNs by Rethinking Their Symmetries

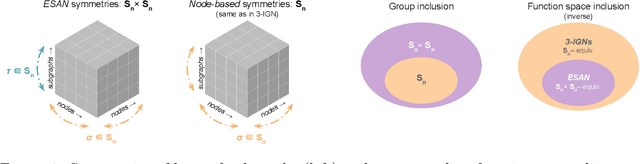
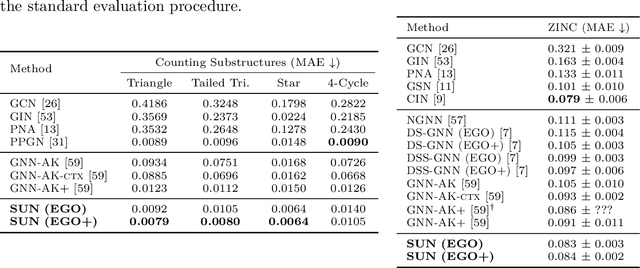
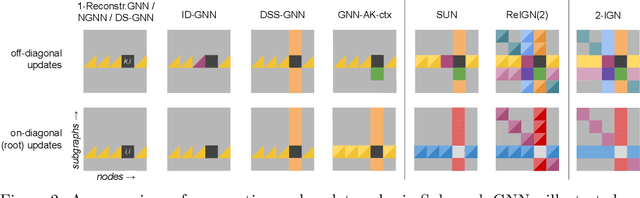
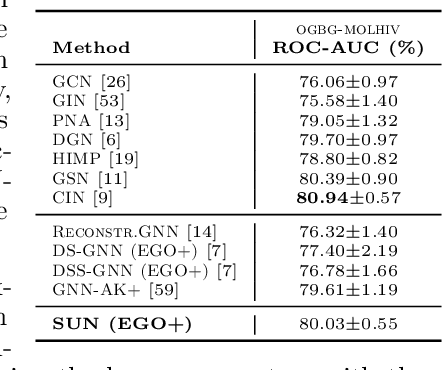
Subgraph GNNs are a recent class of expressive Graph Neural Networks (GNNs) which model graphs as collections of subgraphs. So far, the design space of possible Subgraph GNN architectures as well as their basic theoretical properties are still largely unexplored. In this paper, we study the most prominent form of subgraph methods, which employs node-based subgraph selection policies such as ego-networks or node marking and deletion. We address two central questions: (1) What is the upper-bound of the expressive power of these methods? and (2) What is the family of equivariant message passing layers on these sets of subgraphs?. Our first step in answering these questions is a novel symmetry analysis which shows that modelling the symmetries of node-based subgraph collections requires a significantly smaller symmetry group than the one adopted in previous works. This analysis is then used to establish a link between Subgraph GNNs and Invariant Graph Networks (IGNs). We answer the questions above by first bounding the expressive power of subgraph methods by 3-WL, and then proposing a general family of message-passing layers for subgraph methods that generalises all previous node-based Subgraph GNNs. Finally, we design a novel Subgraph GNN dubbed SUN, which theoretically unifies previous architectures while providing better empirical performance on multiple benchmarks.