Certified Unlearning for Neural Networks

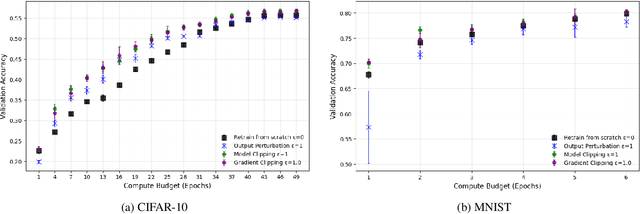
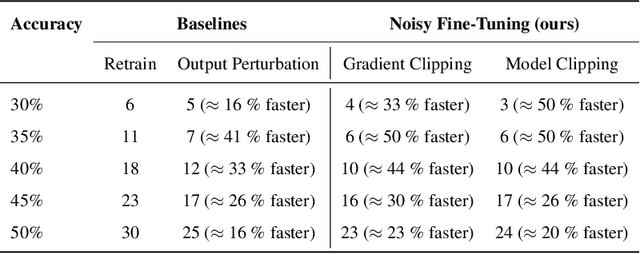
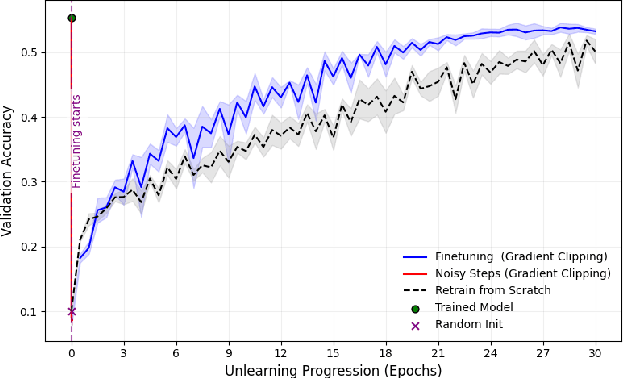
We address the problem of machine unlearning, where the goal is to remove the influence of specific training data from a model upon request, motivated by privacy concerns and regulatory requirements such as the "right to be forgotten." Unfortunately, existing methods rely on restrictive assumptions or lack formal guarantees. To this end, we propose a novel method for certified machine unlearning, leveraging the connection between unlearning and privacy amplification by stochastic post-processing. Our method uses noisy fine-tuning on the retain data, i.e., data that does not need to be removed, to ensure provable unlearning guarantees. This approach requires no assumptions about the underlying loss function, making it broadly applicable across diverse settings. We analyze the theoretical trade-offs in efficiency and accuracy and demonstrate empirically that our method not only achieves formal unlearning guarantees but also performs effectively in practice, outperforming existing baselines. Our code is available at https://github.com/stair-lab/certified-unlearningneural-networks-icml-2025

The Privacy Power of Correlated Noise in Decentralized Learning

Decentralized learning is appealing as it enables the scalable usage of large amounts of distributed data and resources (without resorting to any central entity), while promoting privacy since every user minimizes the direct exposure of their data. Yet, without additional precautions, curious users can still leverage models obtained from their peers to violate privacy. In this paper, we propose Decor, a variant of decentralized SGD with differential privacy (DP) guarantees. Essentially, in Decor, users securely exchange randomness seeds in one communication round to generate pairwise-canceling correlated Gaussian noises, which are injected to protect local models at every communication round. We theoretically and empirically show that, for arbitrary connected graphs, Decor matches the central DP optimal privacy-utility trade-off. We do so under SecLDP, our new relaxation of local DP, which protects all user communications against an external eavesdropper and curious users, assuming that every pair of connected users shares a secret, i.e., an information hidden to all others. The main theoretical challenge is to control the accumulation of non-canceling correlated noise due to network sparsity. We also propose a companion SecLDP privacy accountant for public use.

Asynchronous SGD on Graphs: a Unified Framework for Asynchronous Decentralized and Federated Optimization

Decentralized and asynchronous communications are two popular techniques to speedup communication complexity of distributed machine learning, by respectively removing the dependency over a central orchestrator and the need for synchronization. Yet, combining these two techniques together still remains a challenge. In this paper, we take a step in this direction and introduce Asynchronous SGD on Graphs (AGRAF SGD) -- a general algorithmic framework that covers asynchronous versions of many popular algorithms including SGD, Decentralized SGD, Local SGD, FedBuff, thanks to its relaxed communication and computation assumptions. We provide rates of convergence under much milder assumptions than previous decentralized asynchronous works, while still recovering or even improving over the best know results for all the algorithms covered.

Shuffle SGD is Always Better than SGD: Improved Analysis of SGD with Arbitrary Data Orders

Stochastic Gradient Descent (SGD) algorithms are widely used in optimizing neural networks, with Random Reshuffling (RR) and Single Shuffle (SS) being popular choices for cycling through random or single permutations of the training data. However, the convergence properties of these algorithms in the non-convex case are not fully understood. Existing results suggest that, in realistic training scenarios where the number of epochs is smaller than the training set size, RR may perform worse than SGD. In this paper, we analyze a general SGD algorithm that allows for arbitrary data orderings and show improved convergence rates for non-convex functions. Specifically, our analysis reveals that SGD with random and single shuffling is always faster or at least as good as classical SGD with replacement, regardless of the number of iterations. Overall, our study highlights the benefits of using SGD with random/single shuffling and provides new insights into its convergence properties for non-convex optimization.

Revisiting Gradient Clipping: Stochastic bias and tight convergence guarantees

Gradient clipping is a popular modification to standard (stochastic) gradient descent, at every iteration limiting the gradient norm to a certain value $c >0$. It is widely used for example for stabilizing the training of deep learning models (Goodfellow et al., 2016), or for enforcing differential privacy (Abadi et al., 2016). Despite popularity and simplicity of the clipping mechanism, its convergence guarantees often require specific values of $c$ and strong noise assumptions. In this paper, we give convergence guarantees that show precise dependence on arbitrary clipping thresholds $c$ and show that our guarantees are tight with both deterministic and stochastic gradients. In particular, we show that (i) for deterministic gradient descent, the clipping threshold only affects the higher-order terms of convergence, (ii) in the stochastic setting convergence to the true optimum cannot be guaranteed under the standard noise assumption, even under arbitrary small step-sizes. We give matching upper and lower bounds for convergence of the gradient norm when running clipped SGD, and illustrate these results with experiments.

Convergence of Gradient Descent with Linearly Correlated Noise and Applications to Differentially Private Learning

We study stochastic optimization with linearly correlated noise. Our study is motivated by recent methods for optimization with differential privacy (DP), such as DP-FTRL, which inject noise via matrix factorization mechanisms. We propose an optimization problem that distils key facets of these DP methods and that involves perturbing gradients by linearly correlated noise. We derive improved convergence rates for gradient descent in this framework for convex and non-convex loss functions. Our theoretical analysis is novel and might be of independent interest. We use these convergence rates to develop new, effective matrix factorizations for differentially private optimization, and highlight the benefits of these factorizations theoretically and empirically.

Decentralized Gradient Tracking with Local Steps

Gradient tracking (GT) is an algorithm designed for solving decentralized optimization problems over a network (such as training a machine learning model). A key feature of GT is a tracking mechanism that allows to overcome data heterogeneity between nodes. We develop a novel decentralized tracking mechanism, $K$-GT, that enables communication-efficient local updates in GT while inheriting the data-independence property of GT. We prove a convergence rate for $K$-GT on smooth non-convex functions and prove that it reduces the communication overhead asymptotically by a linear factor $K$, where $K$ denotes the number of local steps. We illustrate the robustness and effectiveness of this heterogeneity correction on convex and non-convex benchmark problems and on a non-convex neural network training task with the MNIST dataset.

Sharper Convergence Guarantees for Asynchronous SGD for Distributed and Federated Learning

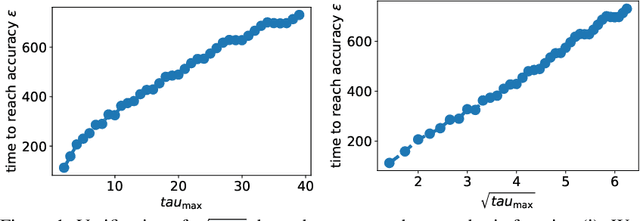
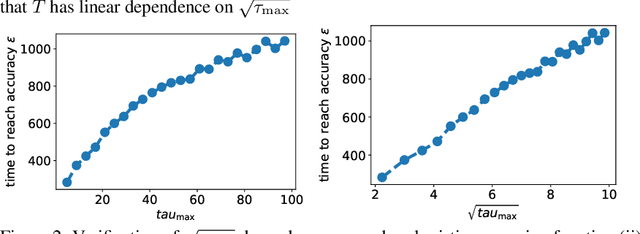
We study the asynchronous stochastic gradient descent algorithm for distributed training over $n$ workers which have varying computation and communication frequency over time. In this algorithm, workers compute stochastic gradients in parallel at their own pace and return those to the server without any synchronization. Existing convergence rates of this algorithm for non-convex smooth objectives depend on the maximum gradient delay $\tau_{\max}$ and show that an $\epsilon$-stationary point is reached after $\mathcal{O}\!\left(\sigma^2\epsilon^{-2}+ \tau_{\max}\epsilon^{-1}\right)$ iterations, where $\sigma$ denotes the variance of stochastic gradients. In this work (i) we obtain a tighter convergence rate of $\mathcal{O}\!\left(\sigma^2\epsilon^{-2}+ \sqrt{\tau_{\max}\tau_{avg}}\epsilon^{-1}\right)$ without any change in the algorithm where $\tau_{avg}$ is the average delay, which can be significantly smaller than $\tau_{\max}$. We also provide (ii) a simple delay-adaptive learning rate scheme, under which asynchronous SGD achieves a convergence rate of $\mathcal{O}\!\left(\sigma^2\epsilon^{-2}+ \tau_{avg}\epsilon^{-1}\right)$, and does not require any extra hyperparameter tuning nor extra communications. Our result allows to show for the first time that asynchronous SGD is always faster than mini-batch SGD. In addition, (iii) we consider the case of heterogeneous functions motivated by federated learning applications and improve the convergence rate by proving a weaker dependence on the maximum delay compared to prior works. In particular, we show that the heterogeneity term in convergence rate is only affected by the average delay within each worker.

Data-heterogeneity-aware Mixing for Decentralized Learning

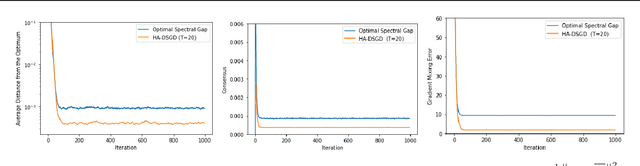
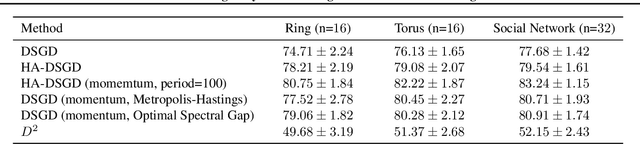
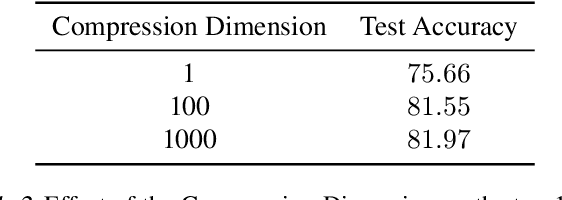
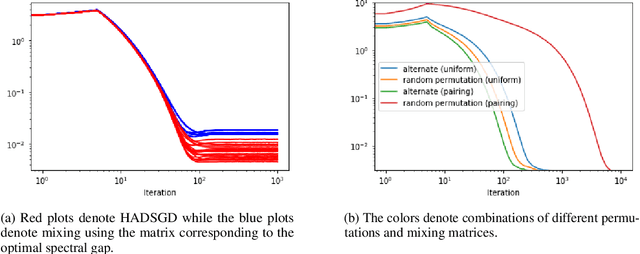
Decentralized learning provides an effective framework to train machine learning models with data distributed over arbitrary communication graphs. However, most existing approaches toward decentralized learning disregard the interaction between data heterogeneity and graph topology. In this paper, we characterize the dependence of convergence on the relationship between the mixing weights of the graph and the data heterogeneity across nodes. We propose a metric that quantifies the ability of a graph to mix the current gradients. We further prove that the metric controls the convergence rate, particularly in settings where the heterogeneity across nodes dominates the stochasticity between updates for a given node. Motivated by our analysis, we propose an approach that periodically and efficiently optimizes the metric using standard convex constrained optimization and sketching techniques. Through comprehensive experiments on standard computer vision and NLP benchmarks, we show that our approach leads to improvement in test performance for a wide range of tasks.

An Improved Analysis of Gradient Tracking for Decentralized Machine Learning

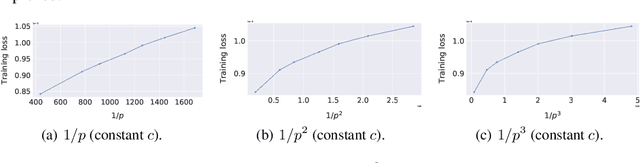
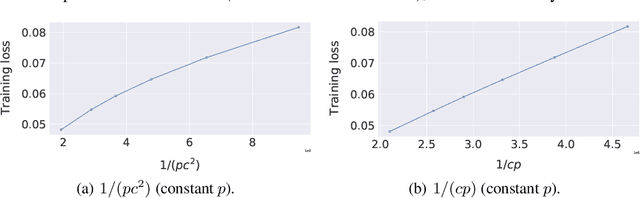
We consider decentralized machine learning over a network where the training data is distributed across $n$ agents, each of which can compute stochastic model updates on their local data. The agent's common goal is to find a model that minimizes the average of all local loss functions. While gradient tracking (GT) algorithms can overcome a key challenge, namely accounting for differences between workers' local data distributions, the known convergence rates for GT algorithms are not optimal with respect to their dependence on the mixing parameter $p$ (related to the spectral gap of the connectivity matrix). We provide a tighter analysis of the GT method in the stochastic strongly convex, convex and non-convex settings. We improve the dependency on $p$ from $\mathcal{O}(p^{-2})$ to $\mathcal{O}(p^{-1}c^{-1})$ in the noiseless case and from $\mathcal{O}(p^{-3/2})$ to $\mathcal{O}(p^{-1/2}c^{-1})$ in the general stochastic case, where $c \geq p$ is related to the negative eigenvalues of the connectivity matrix (and is a constant in most practical applications). This improvement was possible due to a new proof technique which could be of independent interest.