Quantum Hamiltonian-Based Models and the Variational Quantum Thermalizer Algorithm

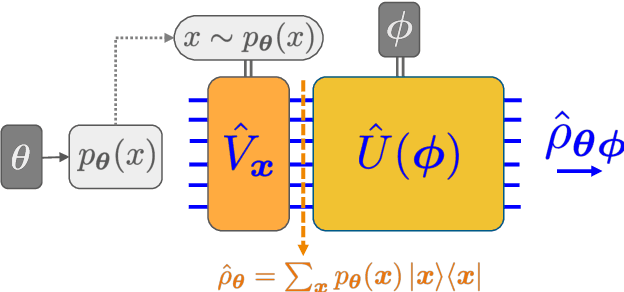
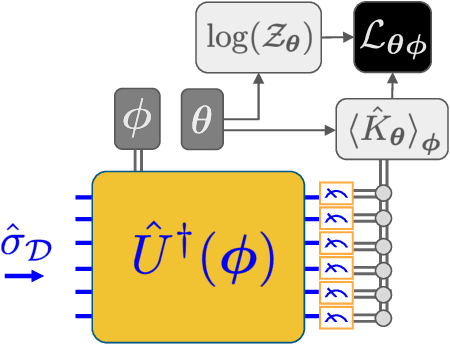
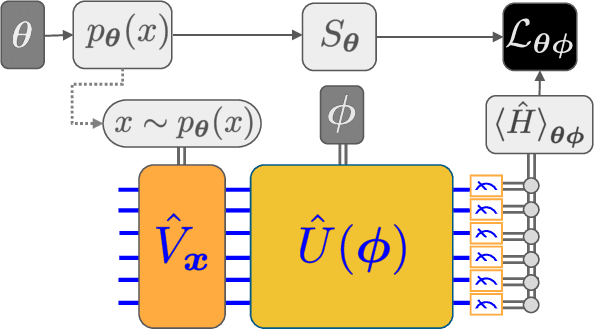
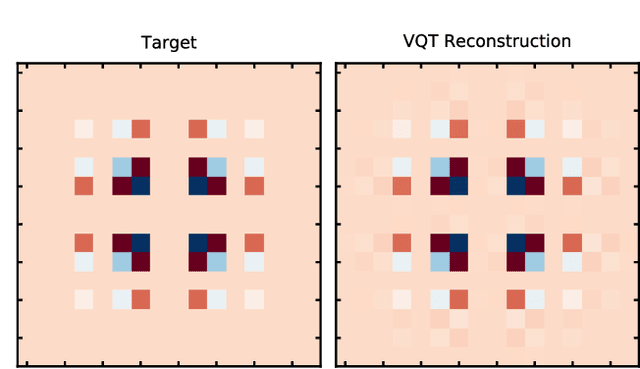
We introduce a new class of generative quantum-neural-network-based models called Quantum Hamiltonian-Based Models (QHBMs). In doing so, we establish a paradigmatic approach for quantum-probabilistic hybrid variational learning, where we efficiently decompose the tasks of learning classical and quantum correlations in a way which maximizes the utility of both classical and quantum processors. In addition, we introduce the Variational Quantum Thermalizer (VQT) for generating the thermal state of a given Hamiltonian and target temperature, a task for which QHBMs are naturally well-suited. The VQT can be seen as a generalization of the Variational Quantum Eigensolver (VQE) to thermal states: we show that the VQT converges to the VQE in the zero temperature limit. We provide numerical results demonstrating the efficacy of these techniques in illustrative examples. We use QHBMs and the VQT on Heisenberg spin systems, we apply QHBMs to learn entanglement Hamiltonians and compression codes in simulated free Bosonic systems, and finally we use the VQT to prepare thermal Fermionic Gaussian states for quantum simulation.

Quantum Graph Neural Networks

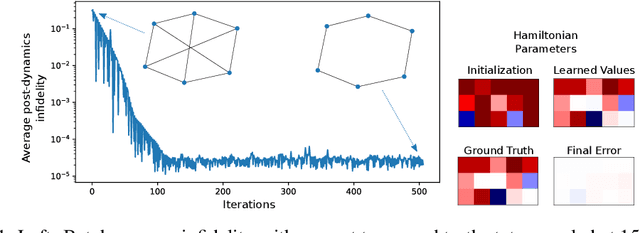
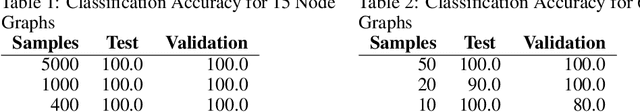
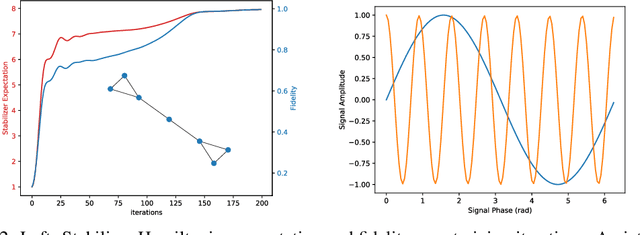
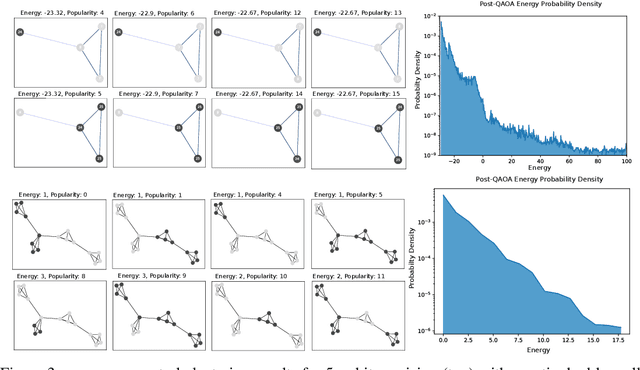
We introduce Quantum Graph Neural Networks (QGNN), a new class of quantum neural network ansatze which are tailored to represent quantum processes which have a graph structure, and are particularly suitable to be executed on distributed quantum systems over a quantum network. Along with this general class of ansatze, we introduce further specialized architectures, namely, Quantum Graph Recurrent Neural Networks (QGRNN) and Quantum Graph Convolutional Neural Networks (QGCNN). We provide four example applications of QGNNs: learning Hamiltonian dynamics of quantum systems, learning how to create multipartite entanglement in a quantum network, unsupervised learning for spectral clustering, and supervised learning for graph isomorphism classification.

TensorNetwork for Machine Learning

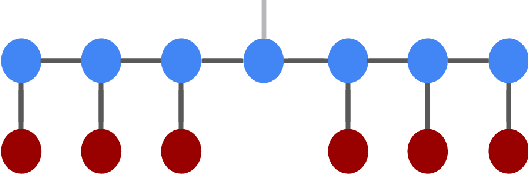
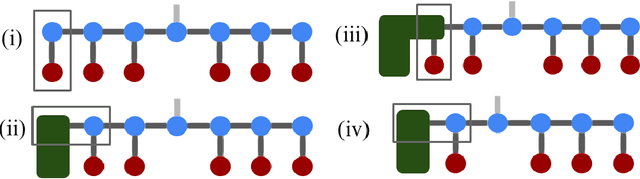
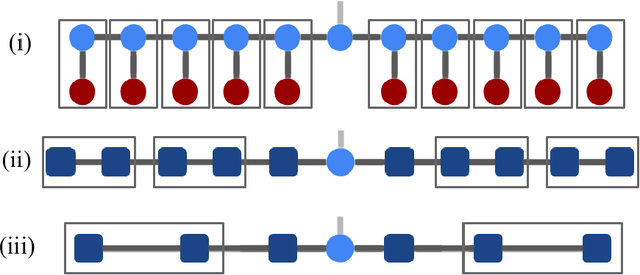
We demonstrate the use of tensor networks for image classification with the TensorNetwork open source library. We explain in detail the encoding of image data into a matrix product state form, and describe how to contract the network in a way that is parallelizable and well-suited to automatic gradients for optimization. Applying the technique to the MNIST and Fashion-MNIST datasets we find out-of-the-box performance of 98% and 88% accuracy, respectively, using the same tensor network architecture. The TensorNetwork library allows us to seamlessly move from CPU to GPU hardware, and we see a factor of more than 10 improvement in computational speed using a GPU.

TensorNetwork on TensorFlow: A Spin Chain Application Using Tree Tensor Networks

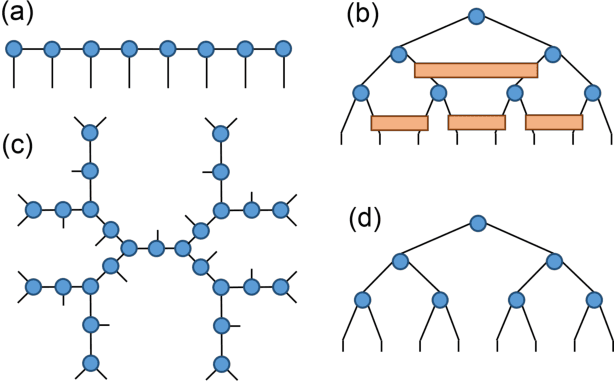
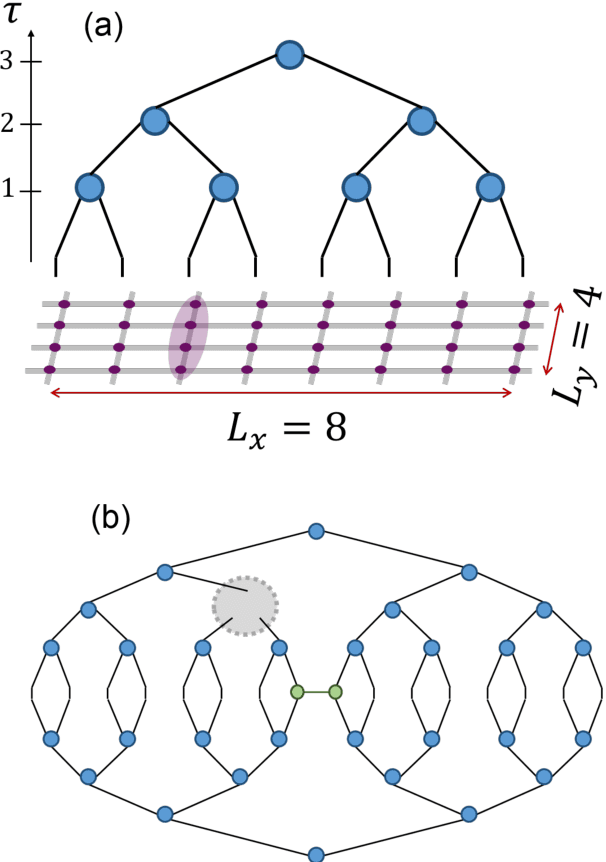
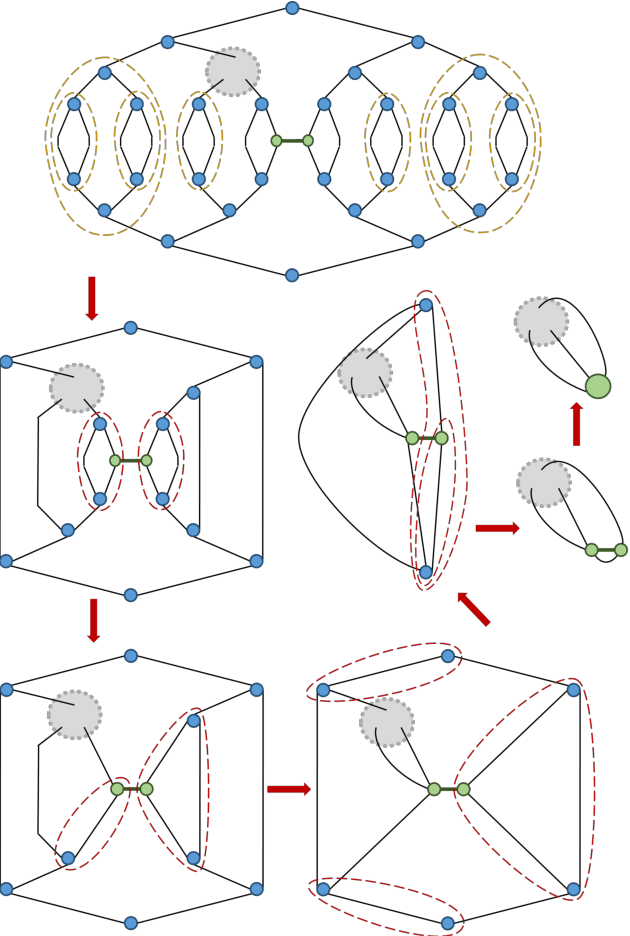
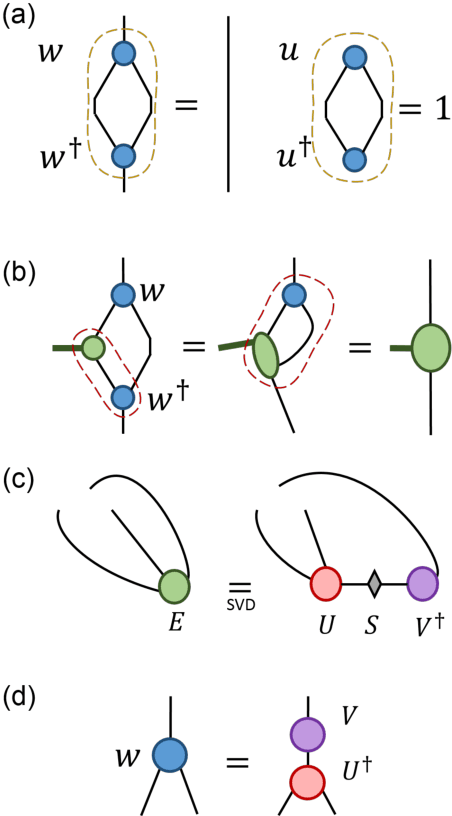
TensorNetwork is an open source library for implementing tensor network algorithms in TensorFlow. We describe a tree tensor network (TTN) algorithm for approximating the ground state of either a periodic quantum spin chain (1D) or a lattice model on a thin torus (2D), and implement the algorithm using TensorNetwork. We use a standard energy minimization procedure over a TTN ansatz with bond dimension $\chi$, with a computational cost that scales as $O(\chi^4)$. Using bond dimension $\chi \in [32,256]$ we compare the use of CPUs with GPUs and observe significant computational speed-ups, up to a factor of $100$, using a GPU and the TensorNetwork library.

TensorNetwork: A Library for Physics and Machine Learning

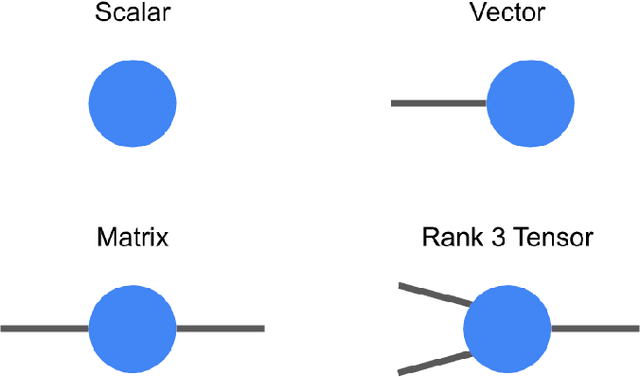
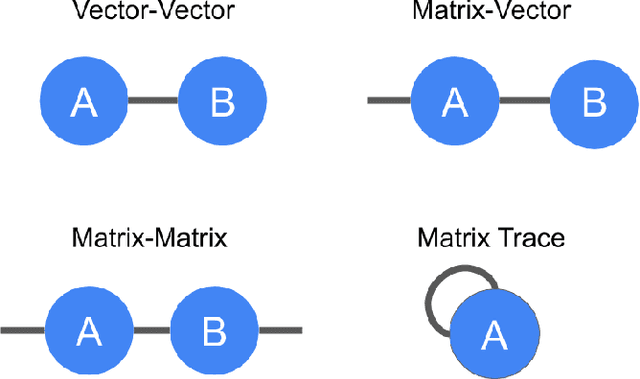
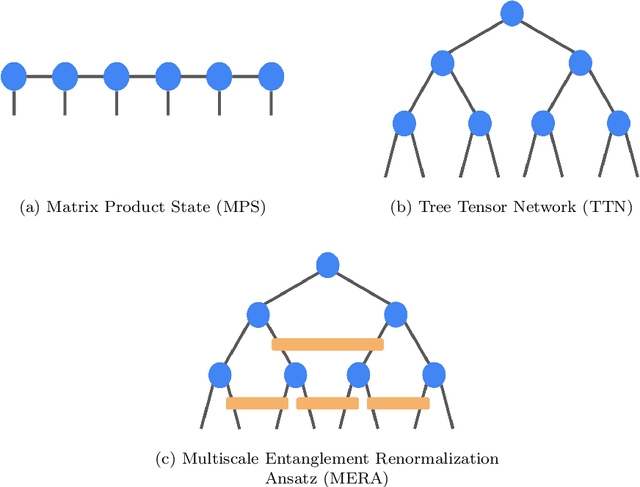
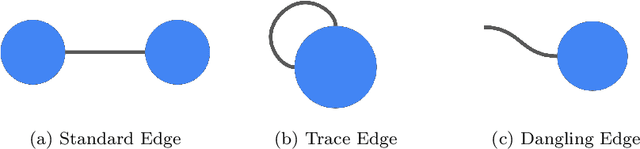
TensorNetwork is an open source library for implementing tensor network algorithms. Tensor networks are sparse data structures originally designed for simulating quantum many-body physics, but are currently also applied in a number of other research areas, including machine learning. We demonstrate the use of the API with applications both physics and machine learning, with details appearing in companion papers.

Theory III: Dynamics and Generalization in Deep Networks - a simple solution

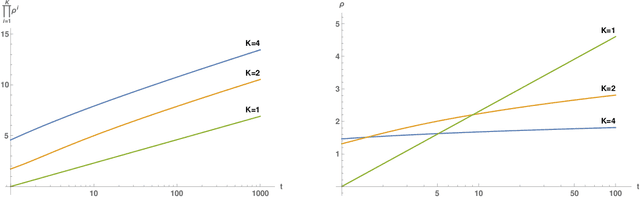
We review recent observations on the dynamical systems induced by gradient descent (GD) methods used for training deep networks and summarize properties of the solutions they converge to. Recent results illuminate the absence of overfitting in the special case of linear networks for binary classification. They prove that minimization of loss functions such as the logistic, the cross-entropy and the exponential loss yields asymptotic convergence to the maximum margin solution for linearly separable datasets, independently of the initial conditions. Here we discuss the case of nonlinear DNNs near zero minima of the empirical loss, under exponential-type and square losses, for several variations of the basic GD algorithm, including a new NMGD version that converges to the minimum norm fixed points. Our main results are: 1) GD algorithms with weight normalization constraint achieve generalization; 2) the fundamental reason for the effectiveness of existing weight and batch normalization techniques is that they are approximate implementations of maximizing the margin under unit norm constraint; 3) even without explicit unit norm constraints, generalization can still be obtained for not-too-deep networks because standard GD is intrinsically consistent with the dynamics of normalized weights. In addition, the balance of the weights across different layers, if present at initialization, is maintained by the gradient flow. In the perspective of these theoretical results, we discuss experimental evidence around the apparent absence of overfitting, that is the observation that the expected classification error does not get worse when increasing the number of parameters. Our explanation focuses on the implicit normalization enforced by algorithms such as batch normalization. In particular, the control of the norm of the weights is related to Halpern iterations for minimum norm solutions.

A Surprising Linear Relationship Predicts Test Performance in Deep Networks

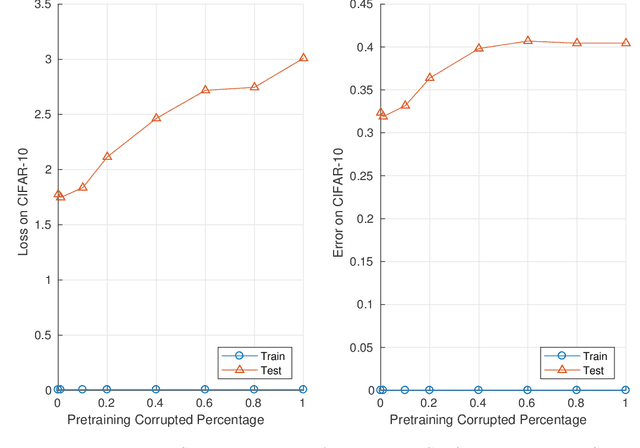
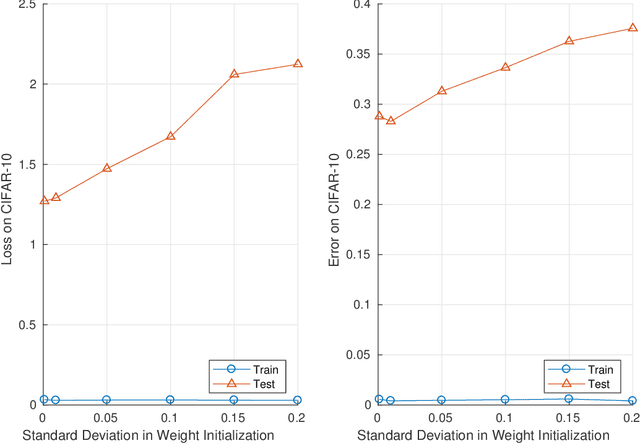
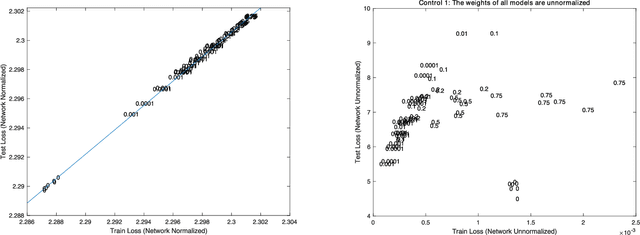
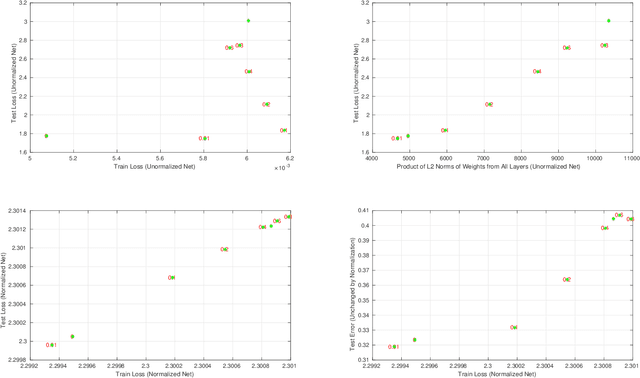
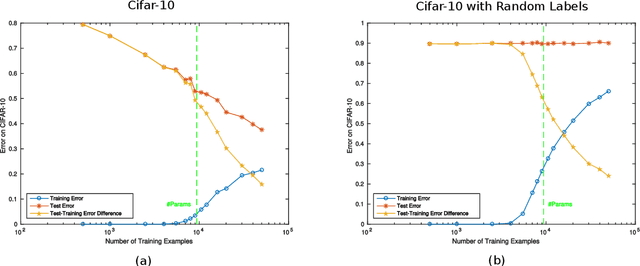
Given two networks with the same training loss on a dataset, when would they have drastically different test losses and errors? Better understanding of this question of generalization may improve practical applications of deep networks. In this paper we show that with cross-entropy loss it is surprisingly simple to induce significantly different generalization performances for two networks that have the same architecture, the same meta parameters and the same training error: one can either pretrain the networks with different levels of "corrupted" data or simply initialize the networks with weights of different Gaussian standard deviations. A corollary of recent theoretical results on overfitting shows that these effects are due to an intrinsic problem of measuring test performance with a cross-entropy/exponential-type loss, which can be decomposed into two components both minimized by SGD -- one of which is not related to expected classification performance. However, if we factor out this component of the loss, a linear relationship emerges between training and test losses. Under this transformation, classical generalization bounds are surprisingly tight: the empirical/training loss is very close to the expected/test loss. Furthermore, the empirical relation between classification error and normalized cross-entropy loss seem to be approximately monotonic

Theory IIIb: Generalization in Deep Networks

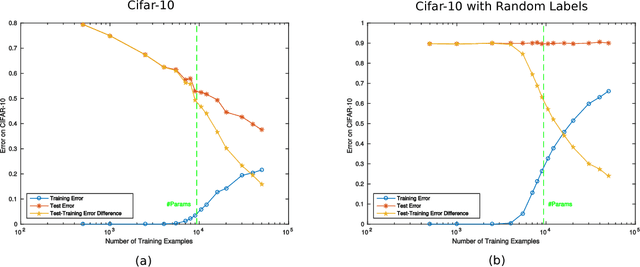
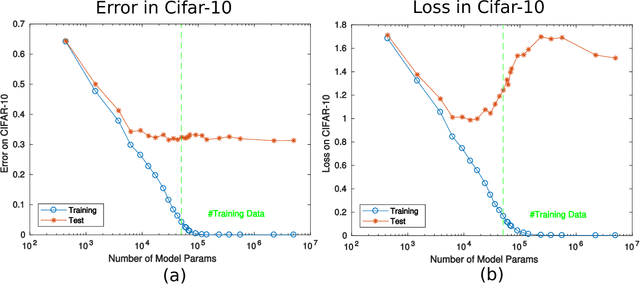
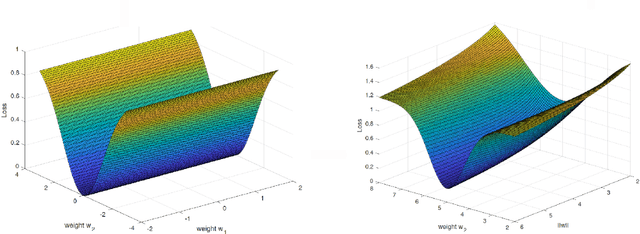
A main puzzle of deep neural networks (DNNs) revolves around the apparent absence of "overfitting", defined in this paper as follows: the expected error does not get worse when increasing the number of neurons or of iterations of gradient descent. This is surprising because of the large capacity demonstrated by DNNs to fit randomly labeled data and the absence of explicit regularization. Recent results by Srebro et al. provide a satisfying solution of the puzzle for linear networks used in binary classification. They prove that minimization of loss functions such as the logistic, the cross-entropy and the exp-loss yields asymptotic, "slow" convergence to the maximum margin solution for linearly separable datasets, independently of the initial conditions. Here we prove a similar result for nonlinear multilayer DNNs near zero minima of the empirical loss. The result holds for exponential-type losses but not for the square loss. In particular, we prove that the weight matrix at each layer of a deep network converges to a minimum norm solution up to a scale factor (in the separable case). Our analysis of the dynamical system corresponding to gradient descent of a multilayer network suggests a simple criterion for ranking the generalization performance of different zero minimizers of the empirical loss.

Theory of Deep Learning III: explaining the non-overfitting puzzle

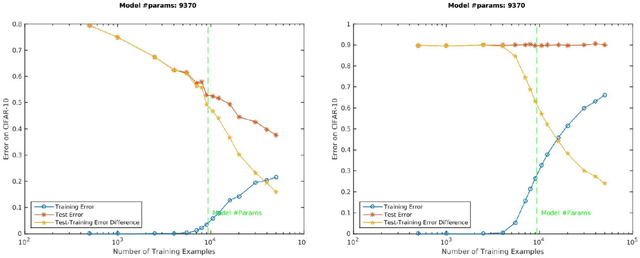
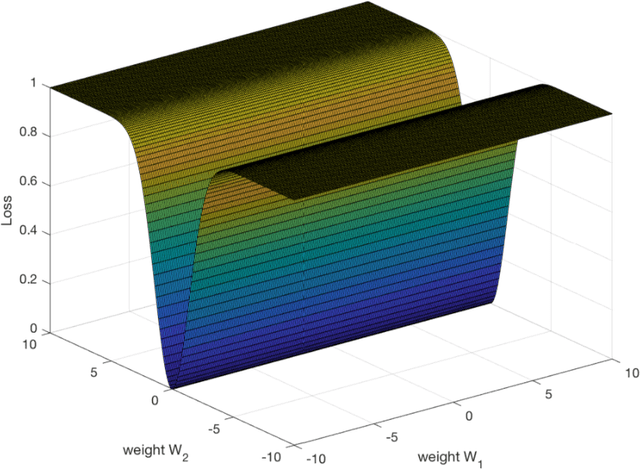
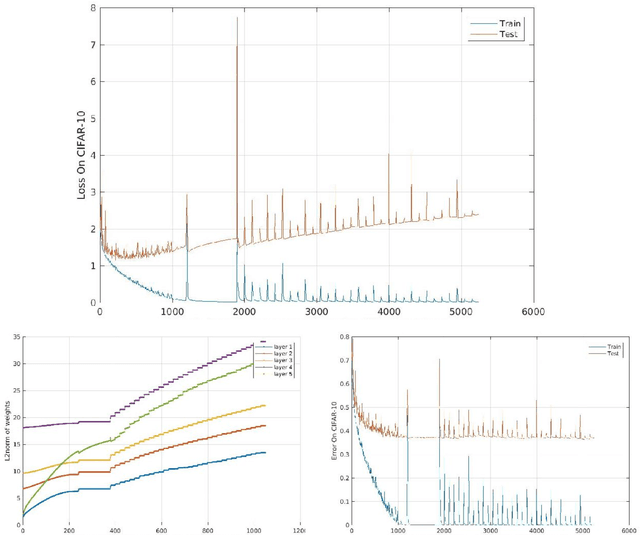
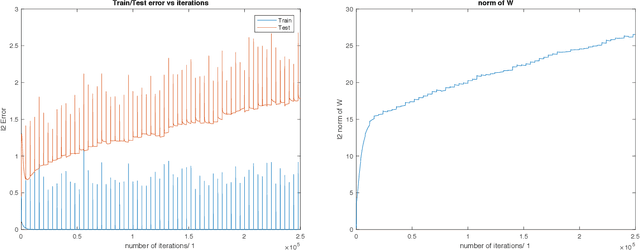
A main puzzle of deep networks revolves around the absence of overfitting despite large overparametrization and despite the large capacity demonstrated by zero training error on randomly labeled data. In this note, we show that the dynamics associated to gradient descent minimization of nonlinear networks is topologically equivalent, near the asymptotically stable minima of the empirical error, to linear gradient system in a quadratic potential with a degenerate (for square loss) or almost degenerate (for logistic or crossentropy loss) Hessian. The proposition depends on the qualitative theory of dynamical systems and is supported by numerical results. Our main propositions extend to deep nonlinear networks two properties of gradient descent for linear networks, that have been recently established (1) to be key to their generalization properties: 1. Gradient descent enforces a form of implicit regularization controlled by the number of iterations, and asymptotically converges to the minimum norm solution for appropriate initial conditions of gradient descent. This implies that there is usually an optimum early stopping that avoids overfitting of the loss. This property, valid for the square loss and many other loss functions, is relevant especially for regression. 2. For classification, the asymptotic convergence to the minimum norm solution implies convergence to the maximum margin solution which guarantees good classification error for "low noise" datasets. This property holds for loss functions such as the logistic and cross-entropy loss independently of the initial conditions. The robustness to overparametrization has suggestive implications for the robustness of the architecture of deep convolutional networks with respect to the curse of dimensionality.