A Hypergraph Neural Network Framework for Learning Hyperedge-Dependent Node Embeddings

In this work, we introduce a hypergraph representation learning framework called Hypergraph Neural Networks (HNN) that jointly learns hyperedge embeddings along with a set of hyperedge-dependent embeddings for each node in the hypergraph. HNN derives multiple embeddings per node in the hypergraph where each embedding for a node is dependent on a specific hyperedge of that node. Notably, HNN is accurate, data-efficient, flexible with many interchangeable components, and useful for a wide range of hypergraph learning tasks. We evaluate the effectiveness of the HNN framework for hyperedge prediction and hypergraph node classification. We find that HNN achieves an overall mean gain of 7.72% and 11.37% across all baseline models and graphs for hyperedge prediction and hypergraph node classification, respectively.

Graph Learning with Localized Neighborhood Fairness

Learning fair graph representations for downstream applications is becoming increasingly important, but existing work has mostly focused on improving fairness at the global level by either modifying the graph structure or objective function without taking into account the local neighborhood of a node. In this work, we formally introduce the notion of neighborhood fairness and develop a computational framework for learning such locally fair embeddings. We argue that the notion of neighborhood fairness is more appropriate since GNN-based models operate at the local neighborhood level of a node. Our neighborhood fairness framework has two main components that are flexible for learning fair graph representations from arbitrary data: the first aims to construct fair neighborhoods for any arbitrary node in a graph and the second enables adaption of these fair neighborhoods to better capture certain application or data-dependent constraints, such as allowing neighborhoods to be more biased towards certain attributes or neighbors in the graph.Furthermore, while link prediction has been extensively studied, we are the first to investigate the graph representation learning task of fair link classification. We demonstrate the effectiveness of the proposed neighborhood fairness framework for a variety of graph machine learning tasks including fair link prediction, link classification, and learning fair graph embeddings. Notably, our approach achieves not only better fairness but also increases the accuracy in the majority of cases across a wide variety of graphs, problem settings, and metrics.

Topological Representations of Local Explanations

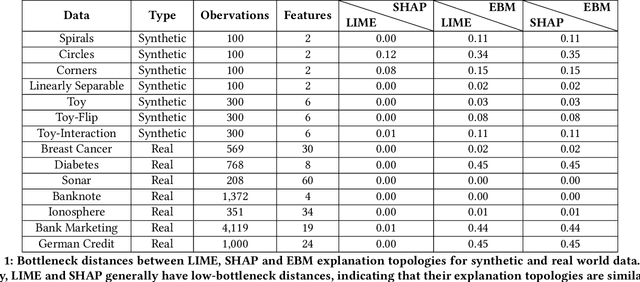
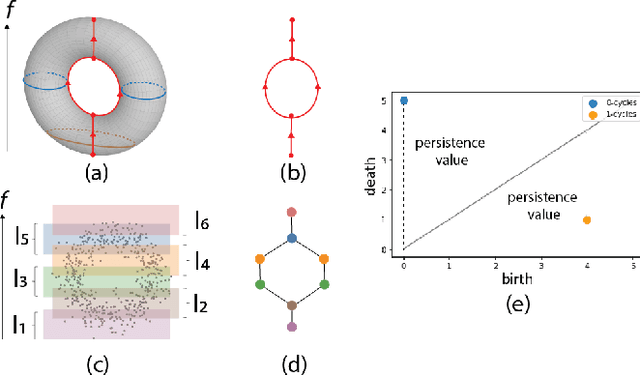
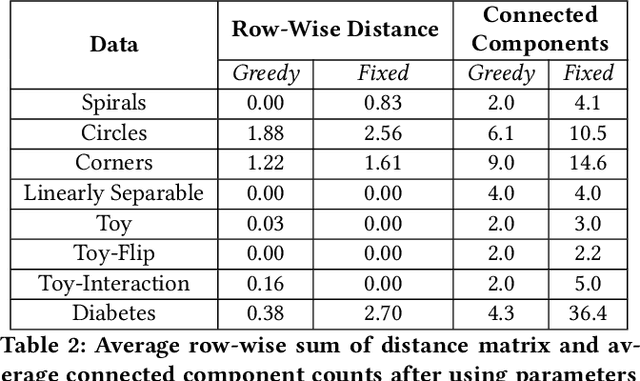
Local explainability methods -- those which seek to generate an explanation for each prediction -- are becoming increasingly prevalent due to the need for practitioners to rationalize their model outputs. However, comparing local explainability methods is difficult since they each generate outputs in various scales and dimensions. Furthermore, due to the stochastic nature of some explainability methods, it is possible for different runs of a method to produce contradictory explanations for a given observation. In this paper, we propose a topology-based framework to extract a simplified representation from a set of local explanations. We do so by first modeling the relationship between the explanation space and the model predictions as a scalar function. Then, we compute the topological skeleton of this function. This topological skeleton acts as a signature for such functions, which we use to compare different explanation methods. We demonstrate that our framework can not only reliably identify differences between explainability techniques but also provides stable representations. Then, we show how our framework can be used to identify appropriate parameters for local explainability methods. Our framework is simple, does not require complex optimizations, and can be broadly applied to most local explanation methods. We believe the practicality and versatility of our approach will help promote topology-based approaches as a tool for understanding and comparing explanation methods.