Sliced-Wasserstein Estimation with Spherical Harmonics as Control Variates

The Sliced-Wasserstein (SW) distance between probability measures is defined as the average of the Wasserstein distances resulting for the associated one-dimensional projections. As a consequence, the SW distance can be written as an integral with respect to the uniform measure on the sphere and the Monte Carlo framework can be employed for calculating the SW distance. Spherical harmonics are polynomials on the sphere that form an orthonormal basis of the set of square-integrable functions on the sphere. Putting these two facts together, a new Monte Carlo method, hereby referred to as Spherical Harmonics Control Variates (SHCV), is proposed for approximating the SW distance using spherical harmonics as control variates. The resulting approach is shown to have good theoretical properties, e.g., a no-error property for Gaussian measures under a certain form of linear dependency between the variables. Moreover, an improved rate of convergence, compared to Monte Carlo, is established for general measures. The convergence analysis relies on the Lipschitz property associated to the SW integrand. Several numerical experiments demonstrate the superior performance of SHCV against state-of-the-art methods for SW distance computation.

Scalable and hyper-parameter-free non-parametric covariate shift adaptation with conditional sampling

Many existing covariate shift adaptation methods estimate sample weights to be used in the risk estimation in order to mitigate the gap between the source and the target distribution. However, non-parametrically estimating the optimal weights typically involves computationally expensive hyper-parameter tuning that is crucial to the final performance. In this paper, we propose a new non-parametric approach to covariate shift adaptation which avoids estimating weights and has no hyper-parameter to be tuned. Our basic idea is to label unlabeled target data according to the $k$-nearest neighbors in the source dataset. Our analysis indicates that setting $k = 1$ is an optimal choice. Thanks to this property, there is no need to tune any hyper-parameters, unlike other non-parametric methods. Moreover, our method achieves a running time quasi-linear in the sample size with a theoretical guarantee, for the first time in the literature to the best of our knowledge. Our results include sharp rates of convergence for estimating the joint probability distribution of the target data. In particular, the variance of our estimators has the same rate of convergence as for standard parametric estimation despite their non-parametric nature. Our numerical experiments show that proposed method brings drastic reduction in the running time with accuracy comparable to that of the state-of-the-art methods.

Sharp error bounds for imbalanced classification: how many examples in the minority class?

When dealing with imbalanced classification data, reweighting the loss function is a standard procedure allowing to equilibrate between the true positive and true negative rates within the risk measure. Despite significant theoretical work in this area, existing results do not adequately address a main challenge within the imbalanced classification framework, which is the negligible size of one class in relation to the full sample size and the need to rescale the risk function by a probability tending to zero. To address this gap, we present two novel contributions in the setting where the rare class probability approaches zero: (1) a non asymptotic fast rate probability bound for constrained balanced empirical risk minimization, and (2) a consistent upper bound for balanced nearest neighbors estimates. Our findings provide a clearer understanding of the benefits of class-weighting in realistic settings, opening new avenues for further research in this field.

A Quadrature Rule combining Control Variates and Adaptive Importance Sampling

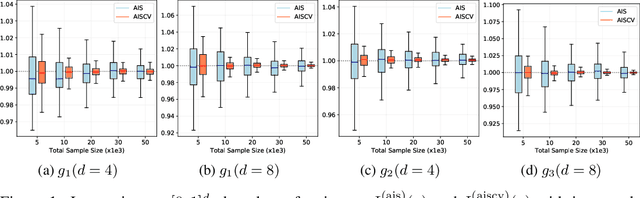
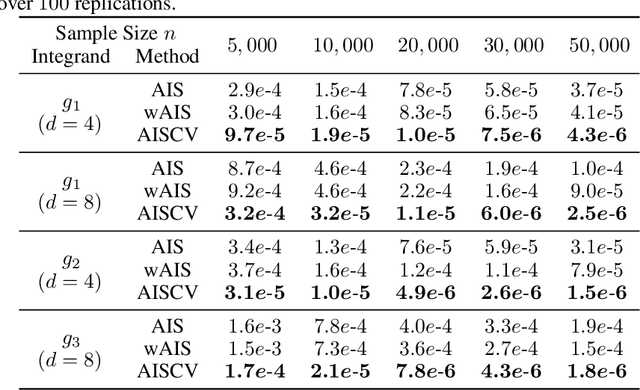
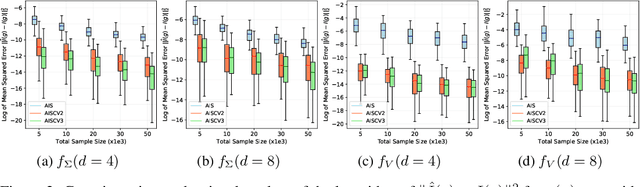
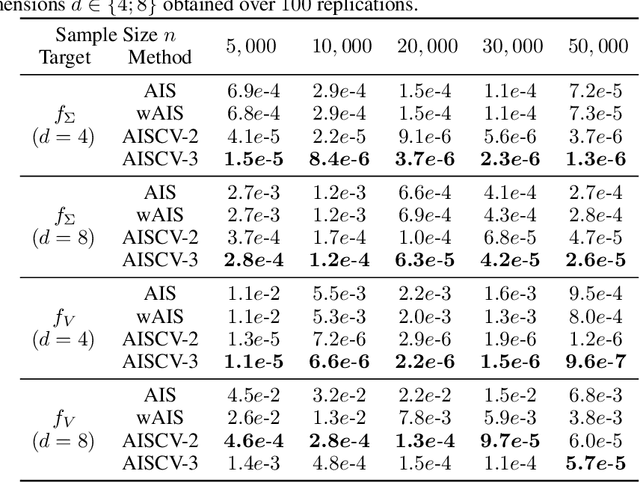
Driven by several successful applications such as in stochastic gradient descent or in Bayesian computation, control variates have become a major tool for Monte Carlo integration. However, standard methods do not allow the distribution of the particles to evolve during the algorithm, as is the case in sequential simulation methods. Within the standard adaptive importance sampling framework, a simple weighted least squares approach is proposed to improve the procedure with control variates. The procedure takes the form of a quadrature rule with adapted quadrature weights to reflect the information brought in by the control variates. The quadrature points and weights do not depend on the integrand, a computational advantage in case of multiple integrands. Moreover, the target density needs to be known only up to a multiplicative constant. Our main result is a non-asymptotic bound on the probabilistic error of the procedure. The bound proves that for improving the estimate's accuracy, the benefits from adaptive importance sampling and control variates can be combined. The good behavior of the method is illustrated empirically on synthetic examples and real-world data for Bayesian linear regression.

Adaptive Importance Sampling meets Mirror Descent: a Bias-variance tradeoff

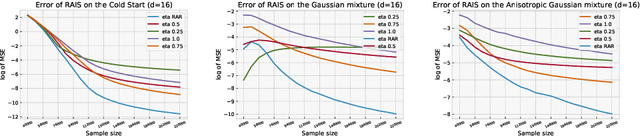
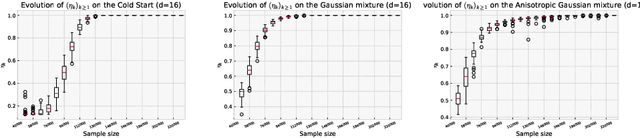
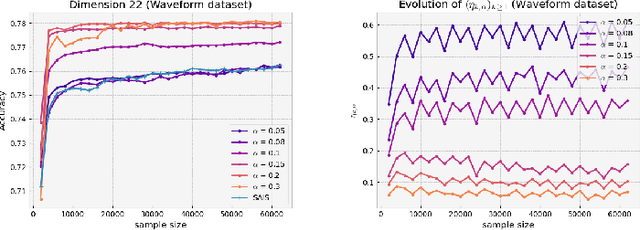
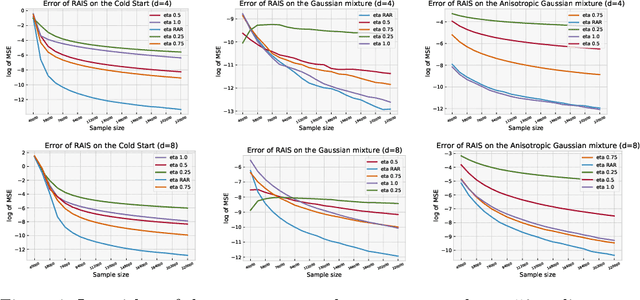
Adaptive importance sampling is a widely spread Monte Carlo technique that uses a re-weighting strategy to iteratively estimate the so-called target distribution. A major drawback of adaptive importance sampling is the large variance of the weights which is known to badly impact the accuracy of the estimates. This paper investigates a regularization strategy whose basic principle is to raise the importance weights at a certain power. This regularization parameter, that might evolve between zero and one during the algorithm, is shown (i) to balance between the bias and the variance and (ii) to be connected to the mirror descent framework. Using a kernel density estimate to build the sampling policy, the uniform convergence is established under mild conditions. Finally, several practical ways to choose the regularization parameter are discussed and the benefits of the proposed approach are illustrated empirically.

Nearest neighbor process: weak convergence and non-asymptotic bound

An empirical measure that results from the nearest neighbors to a given point - the nearest neighbor measure - is introduced and studied as a central statistical quantity. First, the resulting empirical process is shown to satisfy a uniform central limit theorem under a (local) bracketing entropy condition on the underlying class of functions (reflecting the localizing nature of nearest neighbor algorithm). Second a uniform non-asymptotic bound is established under a well-known condition, often refereed to as Vapnik-Chervonenkis, on the uniform entropy numbers.

SGD with Coordinate Sampling: Theory and Practice

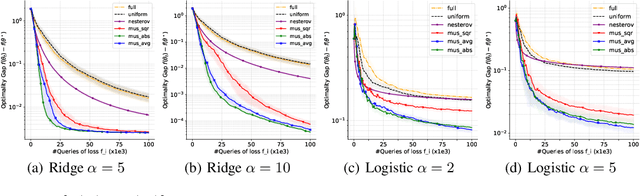
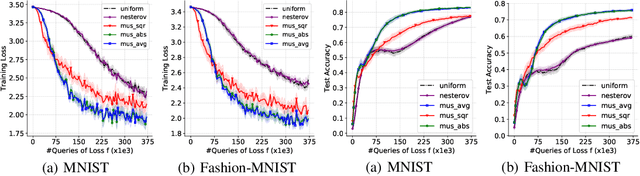
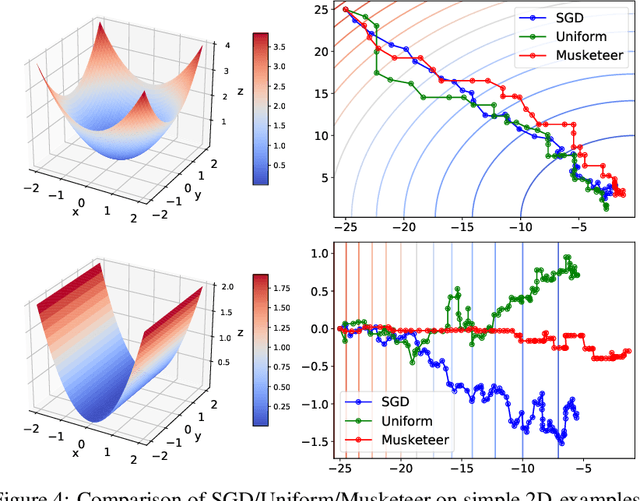
While classical forms of stochastic gradient descent algorithm treat the different coordinates in the same way, a framework allowing for adaptive (non uniform) coordinate sampling is developed to leverage structure in data. In a non-convex setting and including zeroth order gradient estimate, almost sure convergence as well as non-asymptotic bounds are established. Within the proposed framework, we develop an algorithm, MUSKETEER, based on a reinforcement strategy: after collecting information on the noisy gradients, it samples the most promising coordinate (all for one); then it moves along the one direction yielding an important decrease of the objective (one for all). Numerical experiments on both synthetic and real data examples confirm the effectiveness of MUSKETEER in large scale problems.

Nearest Neighbour Based Estimates of Gradients: Sharp Nonasymptotic Bounds and Applications

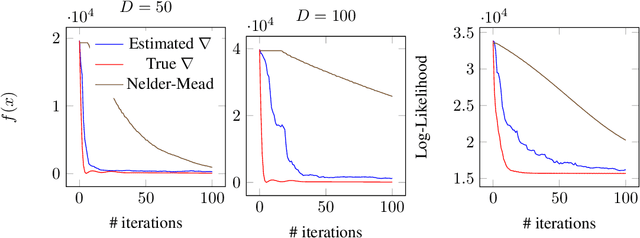
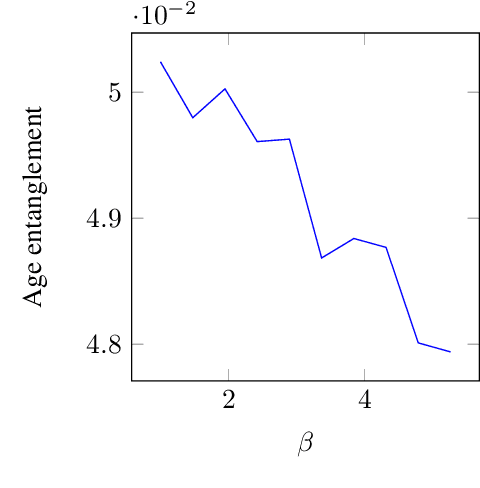
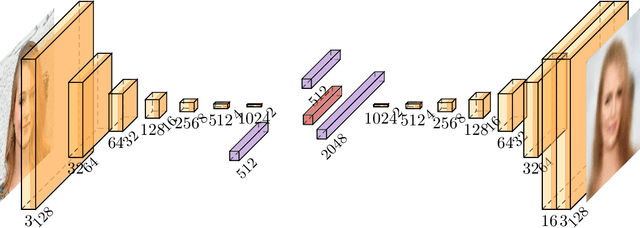
Motivated by a wide variety of applications, ranging from stochastic optimization to dimension reduction through variable selection, the problem of estimating gradients accurately is of crucial importance in statistics and learning theory. We consider here the classic regression setup, where a real valued square integrable r.v. $Y$ is to be predicted upon observing a (possibly high dimensional) random vector $X$ by means of a predictive function $f(X)$ as accurately as possible in the mean-squared sense and study a nearest-neighbour-based pointwise estimate of the gradient of the optimal predictive function, the regression function $m(x)=\mathbb{E}[Y\mid X=x]$. Under classic smoothness conditions combined with the assumption that the tails of $Y-m(X)$ are sub-Gaussian, we prove nonasymptotic bounds improving upon those obtained for alternative estimation methods. Beyond the novel theoretical results established, several illustrative numerical experiments have been carried out. The latter provide strong empirical evidence that the estimation method proposed works very well for various statistical problems involving gradient estimation, namely dimensionality reduction, stochastic gradient descent optimization and quantifying disentanglement.

Conditional independence testing via weighted partial copulas

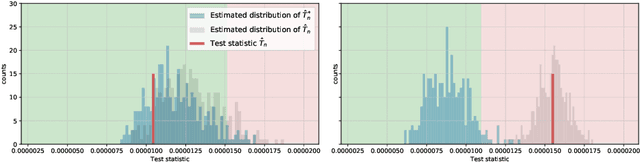
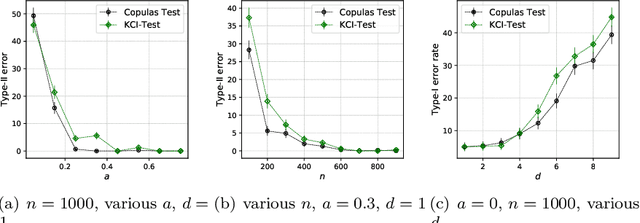
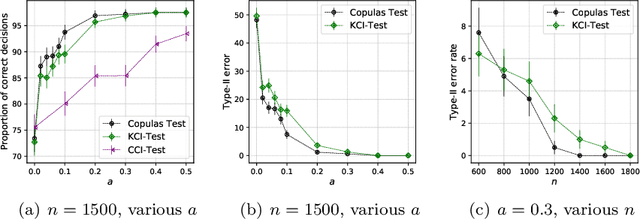
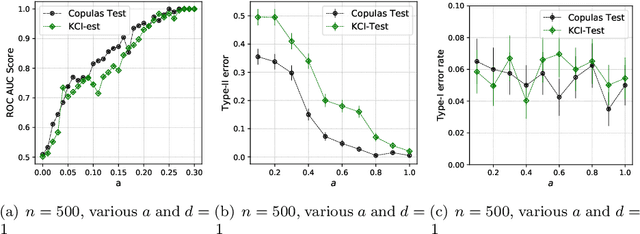
This paper introduces the \textit{weighted partial copula} function for testing conditional independence. The proposed test procedure results from these two ingredients: (i) the test statistic is an explicit Cramer-von Mises transformation of the \textit{weighted partial copula}, (ii) the regions of rejection are computed using a bootstrap procedure which mimics conditional independence by generating samples from the product measure of the estimated conditional marginals. Under conditional independence, the weak convergence of the \textit{weighted partial copula proces}s is established when the marginals are estimated using a smoothed local linear estimator. Finally, an experimental section demonstrates that the proposed test has competitive power compared to recent state-of-the-art methods such as kernel-based test.

Risk bounds when learning infinitely many response functions by ordinary linear regression

Consider the problem of learning a large number of response functions simultaneously based on the same input variables. The training data consist of a single independent random sample of the input variables drawn from a common distribution together with the associated responses. The input variables are mapped into a high-dimensional linear space, called the feature space, and the response functions are modelled as linear functionals of the mapped features, with coefficients calibrated via ordinary least squares. We provide convergence guarantees on the worst-case excess prediction risk by controlling the convergence rate of the excess risk uniformly in the response function. The dimension of the feature map is allowed to tend to infinity with the sample size. The collection of response functions, although potentiallyinfinite, is supposed to have a finite Vapnik-Chervonenkis dimension. The bound derived can be applied when building multiple surrogate models in a reasonable computing time.