Sharp error bounds for imbalanced classification: how many examples in the minority class?

When dealing with imbalanced classification data, reweighting the loss function is a standard procedure allowing to equilibrate between the true positive and true negative rates within the risk measure. Despite significant theoretical work in this area, existing results do not adequately address a main challenge within the imbalanced classification framework, which is the negligible size of one class in relation to the full sample size and the need to rescale the risk function by a probability tending to zero. To address this gap, we present two novel contributions in the setting where the rare class probability approaches zero: (1) a non asymptotic fast rate probability bound for constrained balanced empirical risk minimization, and (2) a consistent upper bound for balanced nearest neighbors estimates. Our findings provide a clearer understanding of the benefits of class-weighting in realistic settings, opening new avenues for further research in this field.

Regular Variation in Hilbert Spaces and Principal Component Analysis for Functional Extremes

Motivated by the increasing availability of data of functional nature, we develop a general probabilistic and statistical framework for extremes of regularly varying random elements $X$ in $L^2[0,1]$. We place ourselves in a Peaks-Over-Threshold framework where a functional extreme is defined as an observation $X$ whose $L^2$-norm $\|X\|$ is comparatively large. Our goal is to propose a dimension reduction framework resulting into finite dimensional projections for such extreme observations. Our contribution is double. First, we investigate the notion of Regular Variation for random quantities valued in a general separable Hilbert space, for which we propose a novel concrete characterization involving solely stochastic convergence of real-valued random variables. Second, we propose a notion of functional Principal Component Analysis (PCA) accounting for the principal `directions' of functional extremes. We investigate the statistical properties of the empirical covariance operator of the angular component of extreme functions, by upper-bounding the Hilbert-Schmidt norm of the estimation error for finite sample sizes. Numerical experiments with simulated and real data illustrate this work.

On Regression in Extreme Regions

In the classic regression problem, the value of a real-valued random variable $Y$ is to be predicted based on the observation of a random vector $X$, taking its values in $\mathbb{R}^d$ with $d\geq 1$ say. The statistical learning problem consists in building a predictive function $\hat{f}:\mathbb{R}^d\to \mathbb{R}$ based on independent copies of the pair $(X,Y)$ so that $Y$ is approximated by $\hat{f}(X)$ with minimum error in the mean-squared sense. Motivated by various applications, ranging from environmental sciences to finance or insurance, special attention is paid here to the case of extreme (i.e. very large) observations $X$. Because of their rarity, they contribute in a negligible manner to the (empirical) error and the predictive performance of empirical quadratic risk minimizers can be consequently very poor in extreme regions. In this paper, we develop a general framework for regression in the extremes. It is assumed that $X$'s conditional distribution given $Y$ belongs to a non parametric class of heavy-tailed probability distributions. It is then shown that an asymptotic notion of risk can be tailored to summarize appropriately predictive performance in extreme regions of the input space. It is also proved that minimization of an empirical and non asymptotic version of this 'extreme risk', based on a fraction of the largest observations solely, yields regression functions with good generalization capacity. In addition, numerical results providing strong empirical evidence of the relevance of the approach proposed are displayed.

Concentration bounds for the empirical angular measure with statistical learning applications

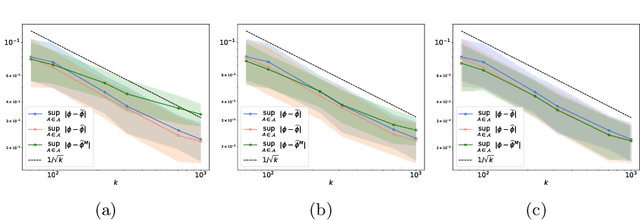
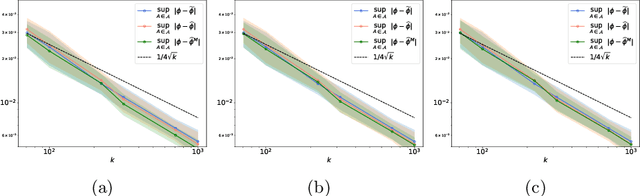
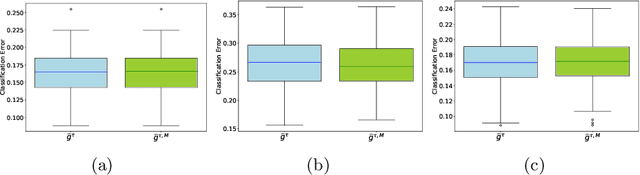
The angular measure on the unit sphere characterizes the first-order dependence structure of the components of a random vector in extreme regions and is defined in terms of standardized margins. Its statistical recovery is an important step in learning problems involving observations far away from the center. In the common situation when the components of the vector have different distributions, the rank transformation offers a convenient and robust way of standardizing data in order to build an empirical version of the angular measure based on the most extreme observations. However, the study of the sampling distribution of the resulting empirical angular measure is challenging. It is the purpose of the paper to establish finite-sample bounds for the maximal deviations between the empirical and true angular measures, uniformly over classes of Borel sets of controlled combinatorial complexity. The bounds are valid with high probability and scale essentially as the square root of the effective sample size, up to a logarithmic factor. Discarding the most extreme observations yields a truncated version of the empirical angular measure for which the logarithmic factor in the concentration bound is replaced by a factor depending on the truncation level. The bounds are applied to provide performance guarantees for two statistical learning procedures tailored to extreme regions of the input space and built upon the empirical angular measure: binary classification in extreme regions through empirical risk minimization and unsupervised anomaly detection through minimum-volume sets of the sphere.

Heavy-tailed Representations, Text Polarity Classification & Data Augmentation

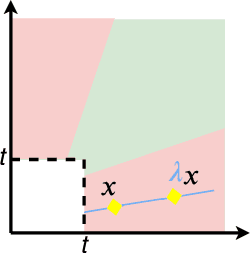
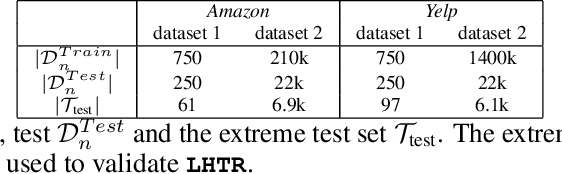
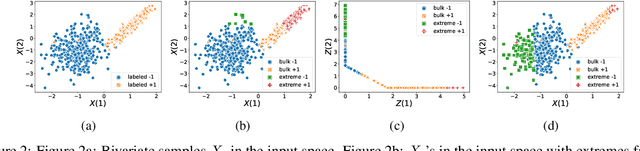
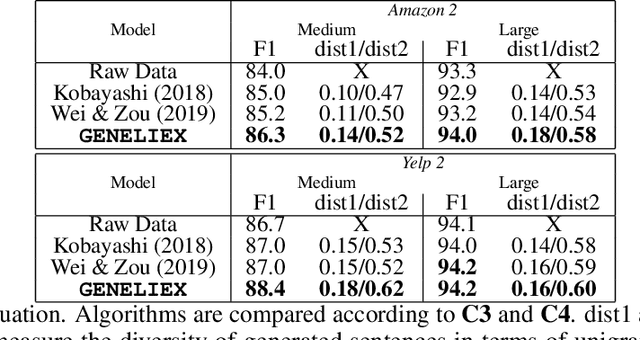
The dominant approaches to text representation in natural language rely on learning embeddings on massive corpora which have convenient properties such as compositionality and distance preservation. In this paper, we develop a novel method to learn a heavy-tailed embedding with desirable regularity properties regarding the distributional tails, which allows to analyze the points far away from the distribution bulk using the framework of multivariate extreme value theory. In particular, a classifier dedicated to the tails of the proposed embedding is obtained which performance outperforms the baseline. This classifier exhibits a scale invariance property which we leverage by introducing a novel text generation method for label preserving dataset augmentation. Numerical experiments on synthetic and real text data demonstrate the relevance of the proposed framework and confirm that this method generates meaningful sentences with controllable attribute, e.g. positive or negative sentiment.

A Multivariate Extreme Value Theory Approach to Anomaly Clustering and Visualization

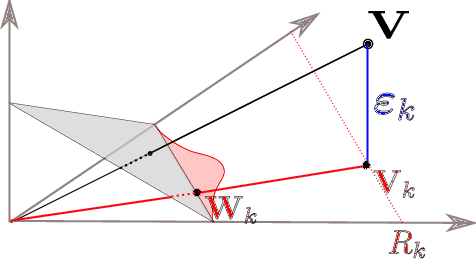
In a wide variety of situations, anomalies in the behaviour of a complex system, whose health is monitored through the observation of a random vector X = (X1,. .. , X d) valued in R d , correspond to the simultaneous occurrence of extreme values for certain subgroups $\alpha$ $\subset$ {1,. .. , d} of variables Xj. Under the heavy-tail assumption, which is precisely appropriate for modeling these phenomena, statistical methods relying on multivariate extreme value theory have been developed in the past few years for identifying such events/subgroups. This paper exploits this approach much further by means of a novel mixture model that permits to describe the distribution of extremal observations and where the anomaly type $\alpha$ is viewed as a latent variable. One may then take advantage of the model by assigning to any extreme point a posterior probability for each anomaly type $\alpha$, defining implicitly a similarity measure between anomalies. It is explained at length how the latter permits to cluster extreme observations and obtain an informative planar representation of anomalies using standard graph-mining tools. The relevance and usefulness of the clustering and 2-d visual display thus designed is illustrated on simulated datasets and on real observations as well, in the aeronautics application domain.

Principal Component Analysis for Multivariate Extremes

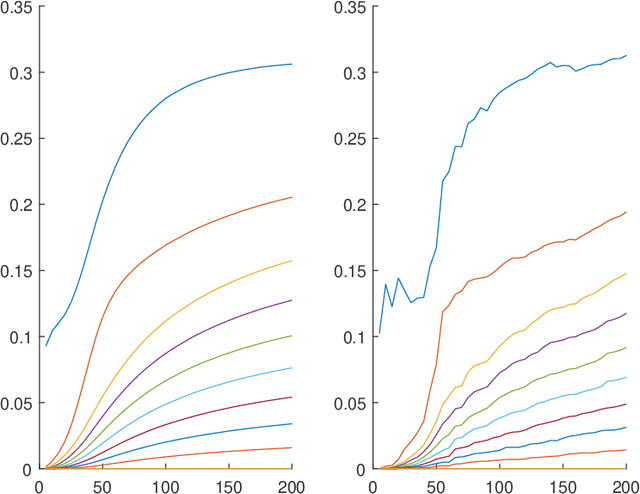
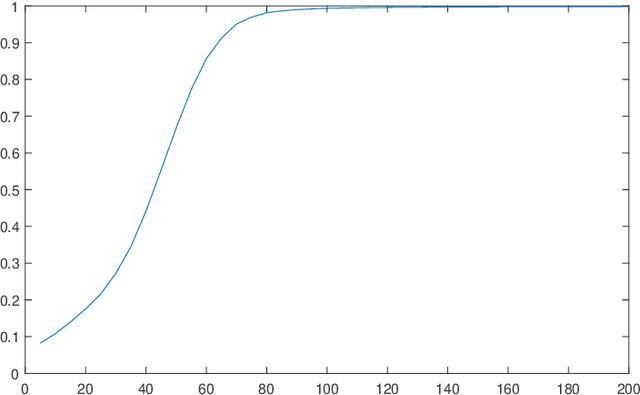
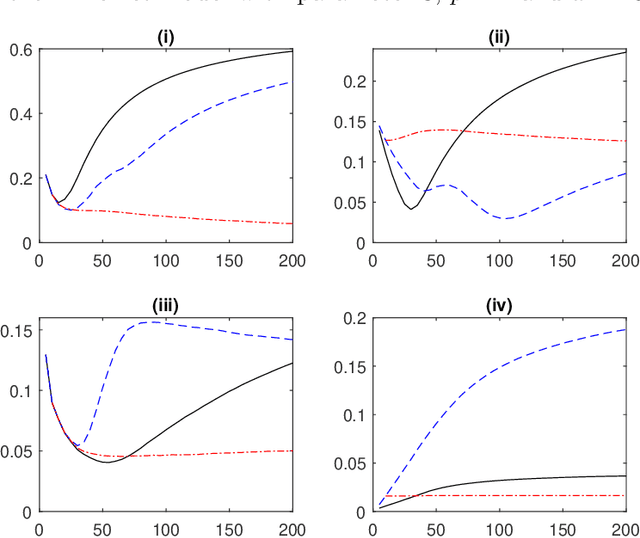
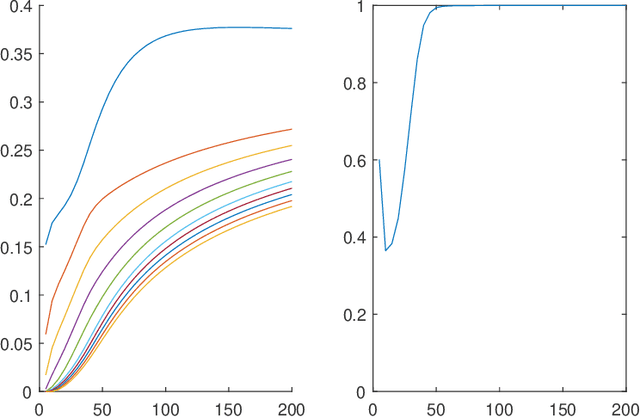
The first order behavior of multivariate heavy-tailed random vectors above large radial thresholds is ruled by a limit measure in a regular variation framework. For a high dimensional vector, a reasonable assumption is that the support of this measure is concentrated on a lower dimensional subspace, meaning that certain linear combinations of the components are much likelier to be large than others. Identifying this subspace and thus reducing the dimension will facilitate a refined statistical analysis. In this work we apply Principal Component Analysis (PCA) to a re-scaled version of radially thresholded observations. Within the statistical learning framework of empirical risk minimization, our main focus is to analyze the squared reconstruction error for the exceedances over large radial thresholds. We prove that the empirical risk converges to the true risk, uniformly over all projection subspaces. As a consequence, the best projection subspace is shown to converge in probability to the optimal one, in terms of the Hausdorff distance between their intersections with the unit sphere. In addition, if the exceedances are re-scaled to the unit ball, we obtain finite sample uniform guarantees to the reconstruction error pertaining to the estimated projection sub-space. Numerical experiments illustrate the relevance of the proposed framework for practical purposes.

Max K-armed bandit: On the ExtremeHunter algorithm and beyond

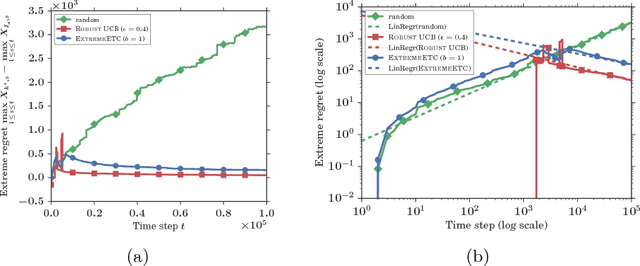
This paper is devoted to the study of the max K-armed bandit problem, which consists in sequentially allocating resources in order to detect extreme values. Our contribution is twofold. We first significantly refine the analysis of the ExtremeHunter algorithm carried out in Carpentier and Valko (2014), and next propose an alternative approach, showing that, remarkably, Extreme Bandits can be reduced to a classical version of the bandit problem to a certain extent. Beyond the formal analysis, these two approaches are compared through numerical experiments.

Sparse Representation of Multivariate Extremes with Applications to Anomaly Ranking

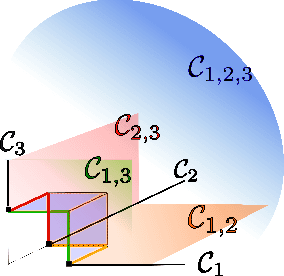
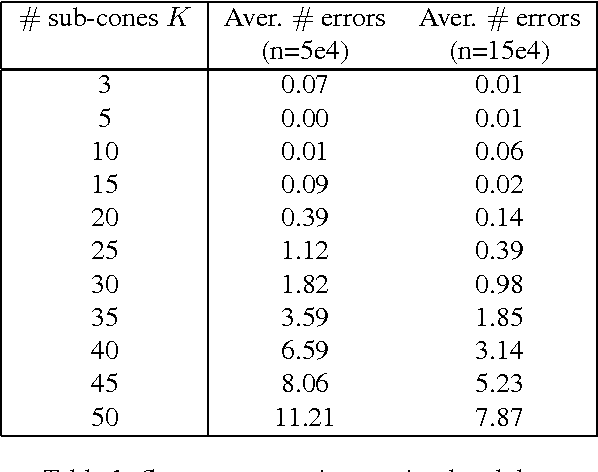
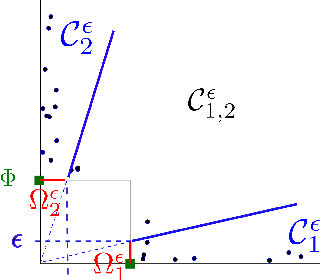
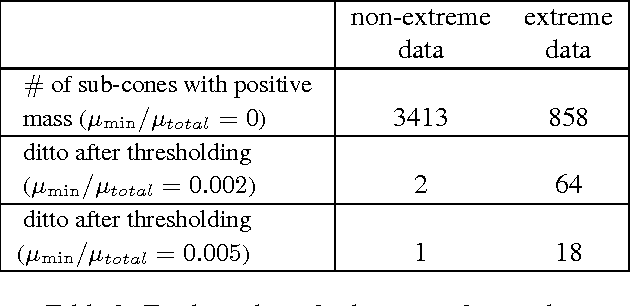
Extremes play a special role in Anomaly Detection. Beyond inference and simulation purposes, probabilistic tools borrowed from Extreme Value Theory (EVT), such as the angular measure, can also be used to design novel statistical learning methods for Anomaly Detection/ranking. This paper proposes a new algorithm based on multivariate EVT to learn how to rank observations in a high dimensional space with respect to their degree of 'abnormality'. The procedure relies on an original dimension-reduction technique in the extreme domain that possibly produces a sparse representation of multivariate extremes and allows to gain insight into the dependence structure thereof, escaping the curse of dimensionality. The representation output by the unsupervised methodology we propose here can be combined with any Anomaly Detection technique tailored to non-extreme data. As it performs linearly with the dimension and almost linearly in the data (in O(dn log n)), it fits to large scale problems. The approach in this paper is novel in that EVT has never been used in its multivariate version in the field of Anomaly Detection. Illustrative experimental results provide strong empirical evidence of the relevance of our approach.

Sparsity in Multivariate Extremes with Applications to Anomaly Detection

Capturing the dependence structure of multivariate extreme events is a major concern in many fields involving the management of risks stemming from multiple sources, e.g. portfolio monitoring, insurance, environmental risk management and anomaly detection. One convenient (non-parametric) characterization of extremal dependence in the framework of multivariate Extreme Value Theory (EVT) is the angular measure, which provides direct information about the probable 'directions' of extremes, that is, the relative contribution of each feature/coordinate of the 'largest' observations. Modeling the angular measure in high dimensional problems is a major challenge for the multivariate analysis of rare events. The present paper proposes a novel methodology aiming at exhibiting a sparsity pattern within the dependence structure of extremes. This is done by estimating the amount of mass spread by the angular measure on representative sets of directions, corresponding to specific sub-cones of $R^d\_+$. This dimension reduction technique paves the way towards scaling up existing multivariate EVT methods. Beyond a non-asymptotic study providing a theoretical validity framework for our method, we propose as a direct application a --first-- anomaly detection algorithm based on multivariate EVT. This algorithm builds a sparse 'normal profile' of extreme behaviours, to be confronted with new (possibly abnormal) extreme observations. Illustrative experimental results provide strong empirical evidence of the relevance of our approach.