Sliced-Wasserstein Estimation with Spherical Harmonics as Control Variates

The Sliced-Wasserstein (SW) distance between probability measures is defined as the average of the Wasserstein distances resulting for the associated one-dimensional projections. As a consequence, the SW distance can be written as an integral with respect to the uniform measure on the sphere and the Monte Carlo framework can be employed for calculating the SW distance. Spherical harmonics are polynomials on the sphere that form an orthonormal basis of the set of square-integrable functions on the sphere. Putting these two facts together, a new Monte Carlo method, hereby referred to as Spherical Harmonics Control Variates (SHCV), is proposed for approximating the SW distance using spherical harmonics as control variates. The resulting approach is shown to have good theoretical properties, e.g., a no-error property for Gaussian measures under a certain form of linear dependency between the variables. Moreover, an improved rate of convergence, compared to Monte Carlo, is established for general measures. The convergence analysis relies on the Lipschitz property associated to the SW integrand. Several numerical experiments demonstrate the superior performance of SHCV against state-of-the-art methods for SW distance computation.

A Quadrature Rule combining Control Variates and Adaptive Importance Sampling

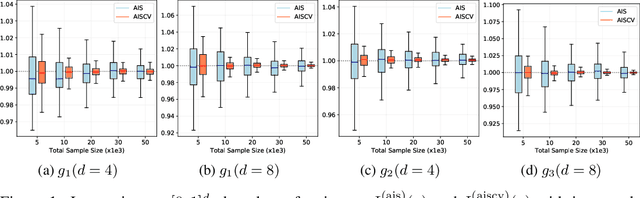
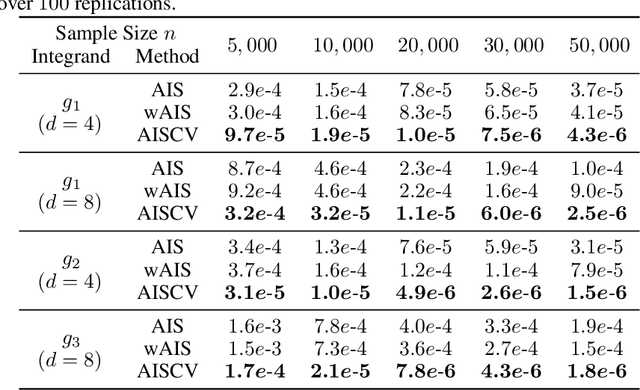
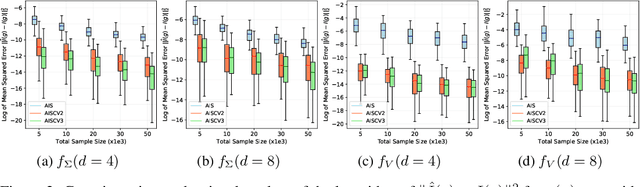
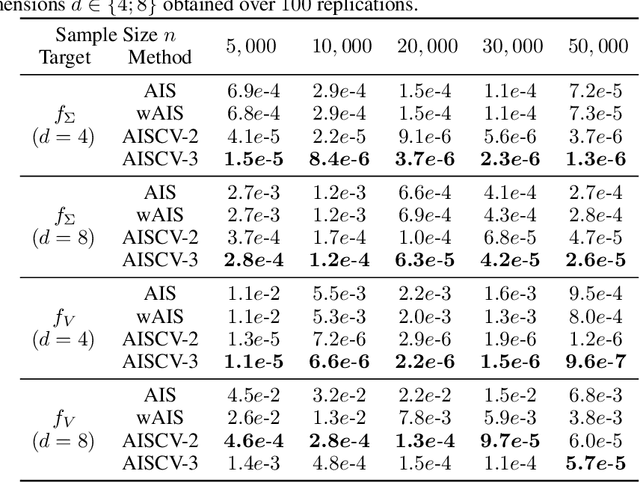
Driven by several successful applications such as in stochastic gradient descent or in Bayesian computation, control variates have become a major tool for Monte Carlo integration. However, standard methods do not allow the distribution of the particles to evolve during the algorithm, as is the case in sequential simulation methods. Within the standard adaptive importance sampling framework, a simple weighted least squares approach is proposed to improve the procedure with control variates. The procedure takes the form of a quadrature rule with adapted quadrature weights to reflect the information brought in by the control variates. The quadrature points and weights do not depend on the integrand, a computational advantage in case of multiple integrands. Moreover, the target density needs to be known only up to a multiplicative constant. Our main result is a non-asymptotic bound on the probabilistic error of the procedure. The bound proves that for improving the estimate's accuracy, the benefits from adaptive importance sampling and control variates can be combined. The good behavior of the method is illustrated empirically on synthetic examples and real-world data for Bayesian linear regression.

Concentration bounds for the empirical angular measure with statistical learning applications

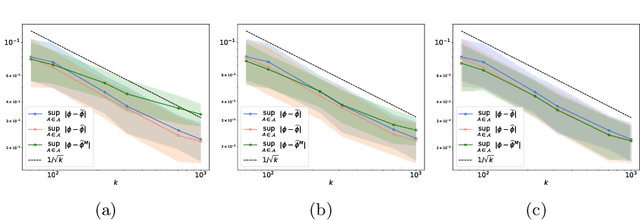
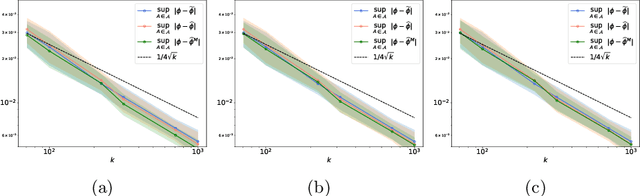
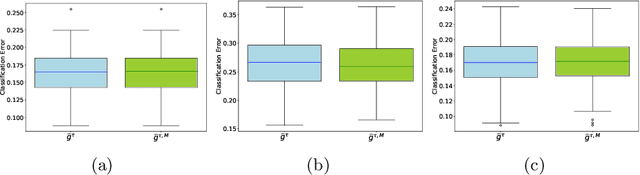
The angular measure on the unit sphere characterizes the first-order dependence structure of the components of a random vector in extreme regions and is defined in terms of standardized margins. Its statistical recovery is an important step in learning problems involving observations far away from the center. In the common situation when the components of the vector have different distributions, the rank transformation offers a convenient and robust way of standardizing data in order to build an empirical version of the angular measure based on the most extreme observations. However, the study of the sampling distribution of the resulting empirical angular measure is challenging. It is the purpose of the paper to establish finite-sample bounds for the maximal deviations between the empirical and true angular measures, uniformly over classes of Borel sets of controlled combinatorial complexity. The bounds are valid with high probability and scale essentially as the square root of the effective sample size, up to a logarithmic factor. Discarding the most extreme observations yields a truncated version of the empirical angular measure for which the logarithmic factor in the concentration bound is replaced by a factor depending on the truncation level. The bounds are applied to provide performance guarantees for two statistical learning procedures tailored to extreme regions of the input space and built upon the empirical angular measure: binary classification in extreme regions through empirical risk minimization and unsupervised anomaly detection through minimum-volume sets of the sphere.

Risk bounds when learning infinitely many response functions by ordinary linear regression

Consider the problem of learning a large number of response functions simultaneously based on the same input variables. The training data consist of a single independent random sample of the input variables drawn from a common distribution together with the associated responses. The input variables are mapped into a high-dimensional linear space, called the feature space, and the response functions are modelled as linear functionals of the mapped features, with coefficients calibrated via ordinary least squares. We provide convergence guarantees on the worst-case excess prediction risk by controlling the convergence rate of the excess risk uniformly in the response function. The dimension of the feature map is allowed to tend to infinity with the sample size. The collection of response functions, although potentiallyinfinite, is supposed to have a finite Vapnik-Chervonenkis dimension. The bound derived can be applied when building multiple surrogate models in a reasonable computing time.

Bayesian inference for bivariate ranks

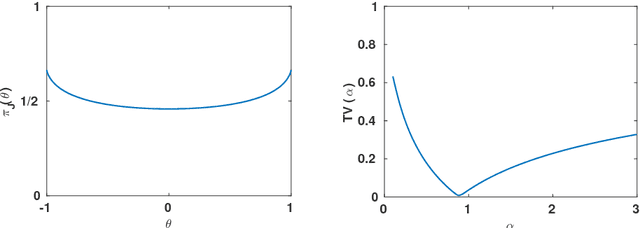
A recommender system based on ranks is proposed, where an expert's ranking of a set of objects and a user's ranking of a subset of those objects are combined to make a prediction of the user's ranking of all objects. The rankings are assumed to be induced by latent continuous variables corresponding to the grades assigned by the expert and the user to the objects. The dependence between the expert and user grades is modelled by a copula in some parametric family. Given a prior distribution on the copula parameter, the user's complete ranking is predicted by the mode of the posterior predictive distribution of the user's complete ranking conditional on the expert's complete and the user's incomplete rankings. Various Markov chain Monte-Carlo algorithms are proposed to approximate the predictive distribution or only its mode. The predictive distribution can be obtained exactly for the Farlie-Gumbel-Morgenstern copula family, providing a benchmark for the approximation accuracy of the algorithms. The method is applied to the MovieLens 100k dataset with a Gaussian copula modelling dependence between the expert's and user's grades.