Rémi Leluc
Sliced-Wasserstein Estimation with Spherical Harmonics as Control Variates
Feb 02, 2024



Abstract:The Sliced-Wasserstein (SW) distance between probability measures is defined as the average of the Wasserstein distances resulting for the associated one-dimensional projections. As a consequence, the SW distance can be written as an integral with respect to the uniform measure on the sphere and the Monte Carlo framework can be employed for calculating the SW distance. Spherical harmonics are polynomials on the sphere that form an orthonormal basis of the set of square-integrable functions on the sphere. Putting these two facts together, a new Monte Carlo method, hereby referred to as Spherical Harmonics Control Variates (SHCV), is proposed for approximating the SW distance using spherical harmonics as control variates. The resulting approach is shown to have good theoretical properties, e.g., a no-error property for Gaussian measures under a certain form of linear dependency between the variables. Moreover, an improved rate of convergence, compared to Monte Carlo, is established for general measures. The convergence analysis relies on the Lipschitz property associated to the SW integrand. Several numerical experiments demonstrate the superior performance of SHCV against state-of-the-art methods for SW distance computation.
Compression with Exact Error Distribution for Federated Learning
Oct 31, 2023Abstract:Compression schemes have been extensively used in Federated Learning (FL) to reduce the communication cost of distributed learning. While most approaches rely on a bounded variance assumption of the noise produced by the compressor, this paper investigates the use of compression and aggregation schemes that produce a specific error distribution, e.g., Gaussian or Laplace, on the aggregated data. We present and analyze different aggregation schemes based on layered quantizers achieving exact error distribution. We provide different methods to leverage the proposed compression schemes to obtain compression-for-free in differential privacy applications. Our general compression methods can recover and improve standard FL schemes with Gaussian perturbations such as Langevin dynamics and randomized smoothing.
MARLIM: Multi-Agent Reinforcement Learning for Inventory Management
Aug 03, 2023Abstract:Maintaining a balance between the supply and demand of products by optimizing replenishment decisions is one of the most important challenges in the supply chain industry. This paper presents a novel reinforcement learning framework called MARLIM, to address the inventory management problem for a single-echelon multi-products supply chain with stochastic demands and lead-times. Within this context, controllers are developed through single or multiple agents in a cooperative setting. Numerical experiments on real data demonstrate the benefits of reinforcement learning methods over traditional baselines.
Membership Inference Attacks via Adversarial Examples
Jul 27, 2022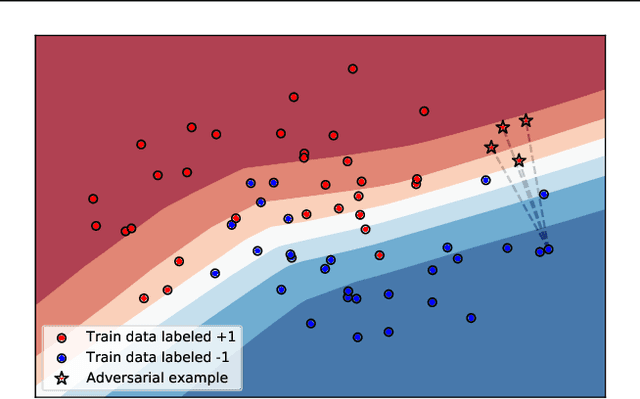

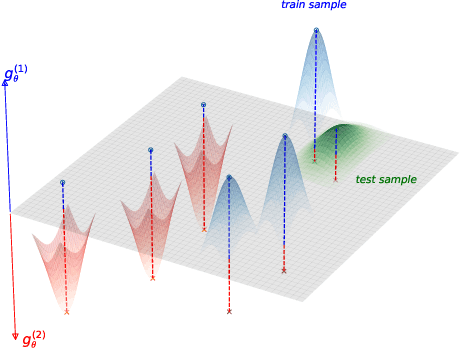
Abstract:The raise of machine learning and deep learning led to significant improvement in several domains. This change is supported by both the dramatic rise in computation power and the collection of large datasets. Such massive datasets often include personal data which can represent a threat to privacy. Membership inference attacks are a novel direction of research which aims at recovering training data used by a learning algorithm. In this paper, we develop a mean to measure the leakage of training data leveraging a quantity appearing as a proxy of the total variation of a trained model near its training samples. We extend our work by providing a novel defense mechanism. Our contributions are supported by empirical evidence through convincing numerical experiments.
A Quadrature Rule combining Control Variates and Adaptive Importance Sampling
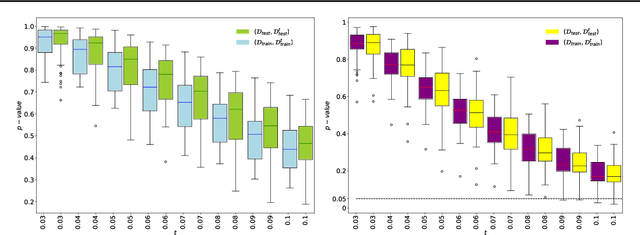
May 24, 2022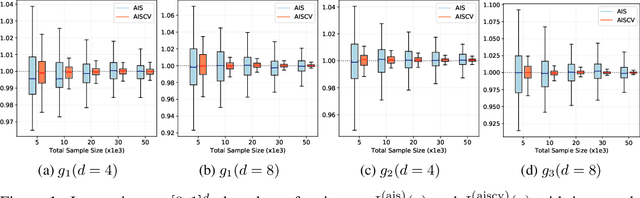
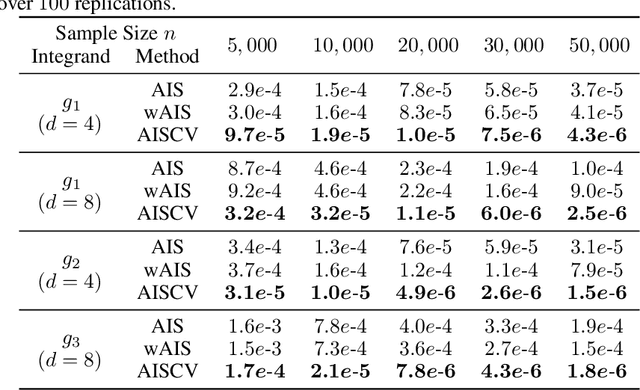
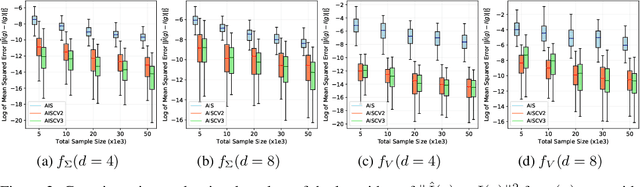
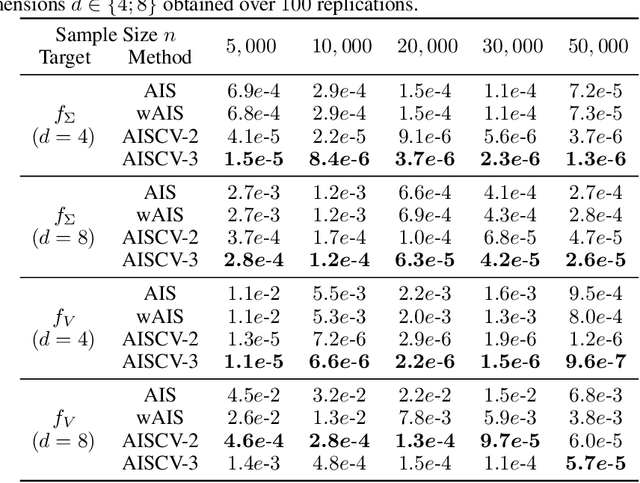
Abstract:Driven by several successful applications such as in stochastic gradient descent or in Bayesian computation, control variates have become a major tool for Monte Carlo integration. However, standard methods do not allow the distribution of the particles to evolve during the algorithm, as is the case in sequential simulation methods. Within the standard adaptive importance sampling framework, a simple weighted least squares approach is proposed to improve the procedure with control variates. The procedure takes the form of a quadrature rule with adapted quadrature weights to reflect the information brought in by the control variates. The quadrature points and weights do not depend on the integrand, a computational advantage in case of multiple integrands. Moreover, the target density needs to be known only up to a multiplicative constant. Our main result is a non-asymptotic bound on the probabilistic error of the procedure. The bound proves that for improving the estimate's accuracy, the benefits from adaptive importance sampling and control variates can be combined. The good behavior of the method is illustrated empirically on synthetic examples and real-world data for Bayesian linear regression.
SGD with Coordinate Sampling: Theory and Practice
May 25, 2021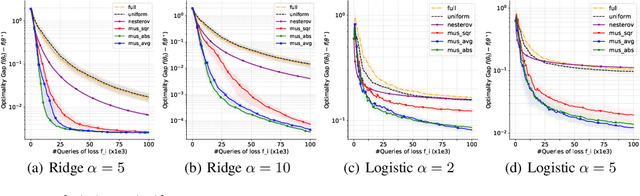

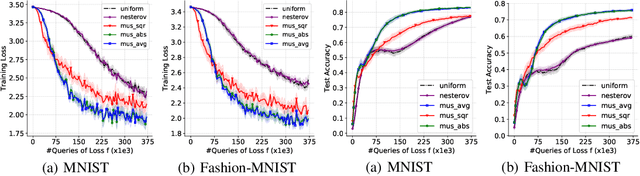
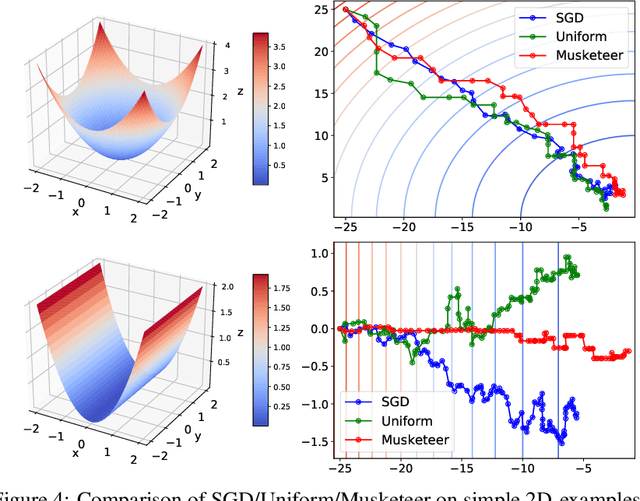
Abstract:While classical forms of stochastic gradient descent algorithm treat the different coordinates in the same way, a framework allowing for adaptive (non uniform) coordinate sampling is developed to leverage structure in data. In a non-convex setting and including zeroth order gradient estimate, almost sure convergence as well as non-asymptotic bounds are established. Within the proposed framework, we develop an algorithm, MUSKETEER, based on a reinforcement strategy: after collecting information on the noisy gradients, it samples the most promising coordinate (all for one); then it moves along the one direction yielding an important decrease of the objective (one for all). Numerical experiments on both synthetic and real data examples confirm the effectiveness of MUSKETEER in large scale problems.
Informative Clusters for Multivariate Extremes
Aug 13, 2020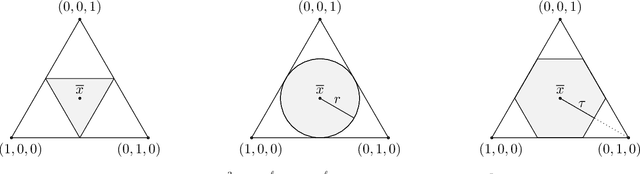
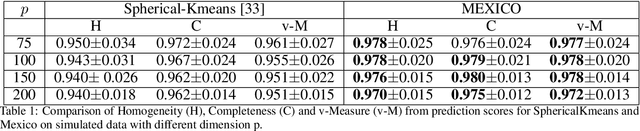
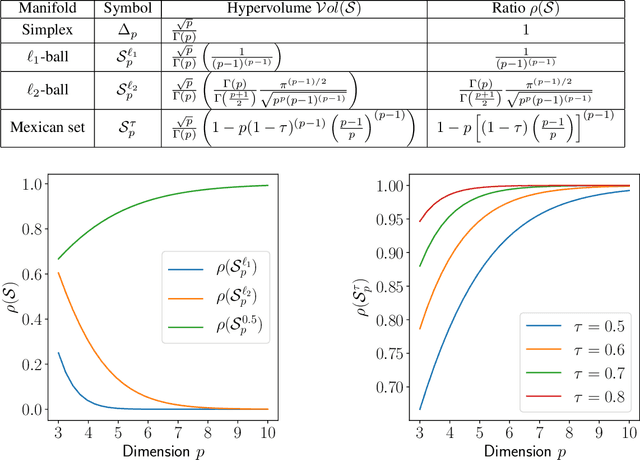
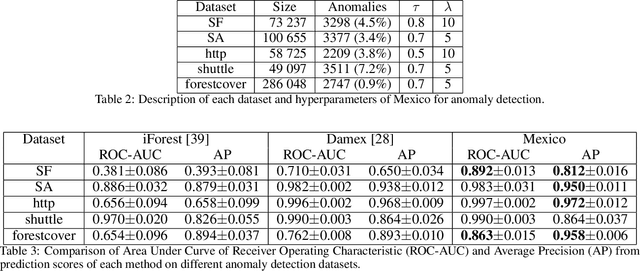
Abstract:Capturing the dependence structure of multivariate extreme data is a major challenge in many fields involving the management of risks that come from multiple sources, e.g., portfolio monitoring, environmental risk management, insurance and anomaly detection. The present paper develops a novel optimization-based approach called MEXICO, standing for Multivariate EXtreme Informative Clustering by Optimization. It aims at exhibiting a sparsity pattern within the dependence structure of extremes. This is achieved by estimating some disjoint clusters of features that tend to be large simultaneously through an optimization method on the probability simplex. This dimension reduction technique can be applied to statistical learning tasks such as feature clustering and anomaly detection. Numerical experiments provide strong empirical evidence of the relevance of our approach.
Towards Asymptotic Optimality with Conditioned Stochastic Gradient Descent
Jun 04, 2020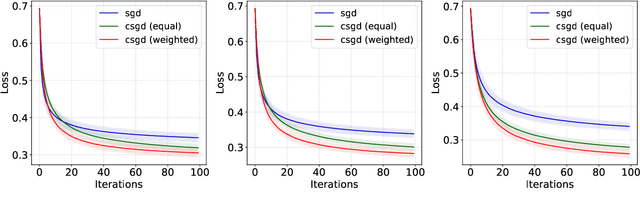
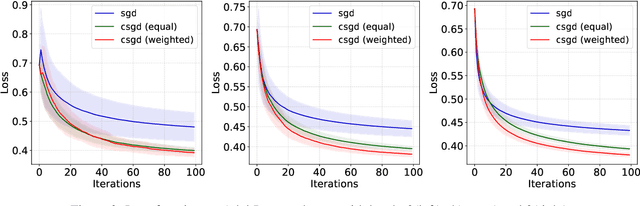
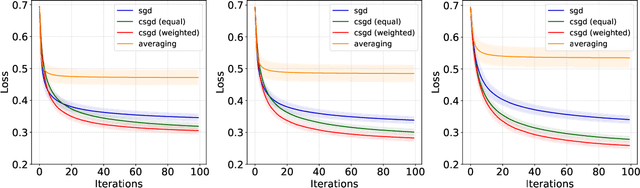
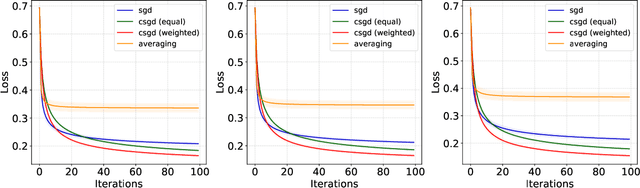
Abstract:In this paper, we investigate a general class of stochastic gradient descent (SGD) algorithms, called conditioned SGD, based on a preconditioning of the gradient direction. Under some mild assumptions, namely the $L$-smoothness of the objective function and some weak growth condition on the noise, we establish the almost sure convergence and the asymptotic normality for a broad class of conditioning matrices. In particular, when the conditioning matrix is an estimate of the inverse Hessian at the optimal point, the algorithm is proved to be asymptotically optimal. The benefits of this approach are validated on simulated and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge