Scalable and hyper-parameter-free non-parametric covariate shift adaptation with conditional sampling

Many existing covariate shift adaptation methods estimate sample weights to be used in the risk estimation in order to mitigate the gap between the source and the target distribution. However, non-parametrically estimating the optimal weights typically involves computationally expensive hyper-parameter tuning that is crucial to the final performance. In this paper, we propose a new non-parametric approach to covariate shift adaptation which avoids estimating weights and has no hyper-parameter to be tuned. Our basic idea is to label unlabeled target data according to the $k$-nearest neighbors in the source dataset. Our analysis indicates that setting $k = 1$ is an optimal choice. Thanks to this property, there is no need to tune any hyper-parameters, unlike other non-parametric methods. Moreover, our method achieves a running time quasi-linear in the sample size with a theoretical guarantee, for the first time in the literature to the best of our knowledge. Our results include sharp rates of convergence for estimating the joint probability distribution of the target data. In particular, the variance of our estimators has the same rate of convergence as for standard parametric estimation despite their non-parametric nature. Our numerical experiments show that proposed method brings drastic reduction in the running time with accuracy comparable to that of the state-of-the-art methods.

Is the Performance of My Deep Network Too Good to Be True? A Direct Approach to Estimating the Bayes Error in Binary Classification

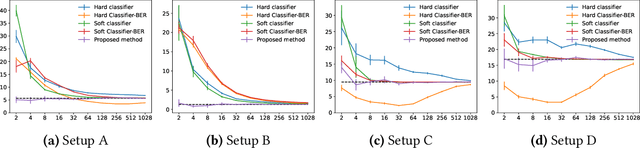
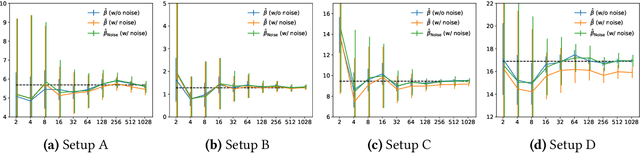
There is a fundamental limitation in the prediction performance that a machine learning model can achieve due to the inevitable uncertainty of the prediction target. In classification problems, this can be characterized by the Bayes error, which is the best achievable error with any classifier. The Bayes error can be used as a criterion to evaluate classifiers with state-of-the-art performance and can be used to detect test set overfitting. We propose a simple and direct Bayes error estimator, where we just take the mean of the labels that show \emph{uncertainty} of the classes. Our flexible approach enables us to perform Bayes error estimation even for weakly supervised data. In contrast to others, our method is model-free and even instance-free. Moreover, it has no hyperparameters and gives a more accurate estimate of the Bayes error than classifier-based baselines. Experiments using our method suggest that a recently proposed classifier, the Vision Transformer, may have already reached the Bayes error for certain benchmark datasets.

Mediated Uncoupled Learning: Learning Functions without Direct Input-output Correspondences

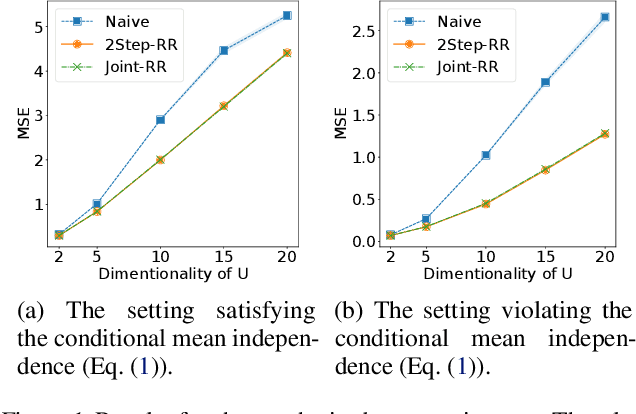
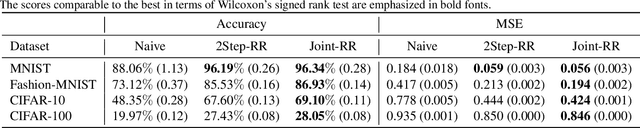
Ordinary supervised learning is useful when we have paired training data of input $X$ and output $Y$. However, such paired data can be difficult to collect in practice. In this paper, we consider the task of predicting $Y$ from $X$ when we have no paired data of them, but we have two separate, independent datasets of $X$ and $Y$ each observed with some mediating variable $U$, that is, we have two datasets $S_X = \{(X_i, U_i)\}$ and $S_Y = \{(U'_j, Y'_j)\}$. A naive approach is to predict $U$ from $X$ using $S_X$ and then $Y$ from $U$ using $S_Y$, but we show that this is not statistically consistent. Moreover, predicting $U$ can be more difficult than predicting $Y$ in practice, e.g., when $U$ has higher dimensionality. To circumvent the difficulty, we propose a new method that avoids predicting $U$ but directly learns $Y = f(X)$ by training $f(X)$ with $S_{X}$ to predict $h(U)$ which is trained with $S_{Y}$ to approximate $Y$. We prove statistical consistency and error bounds of our method and experimentally confirm its practical usefulness.

A One-step Approach to Covariate Shift Adaptation

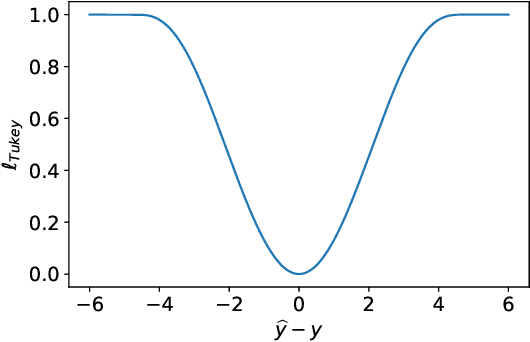
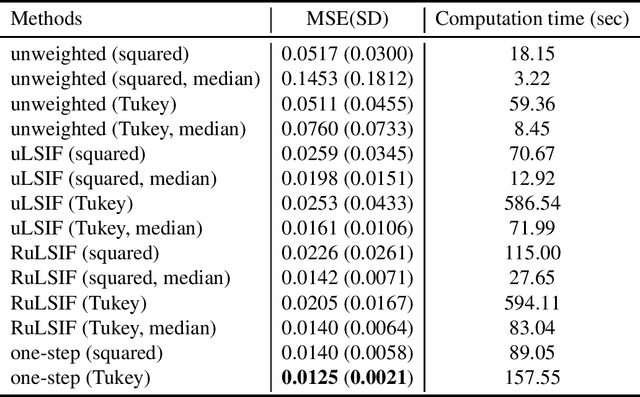
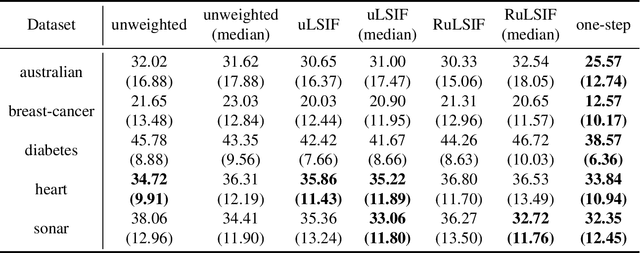
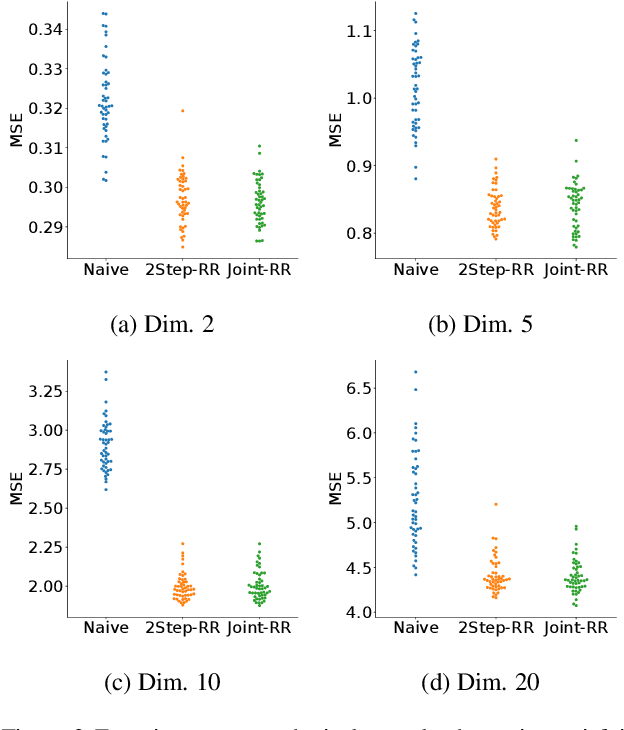
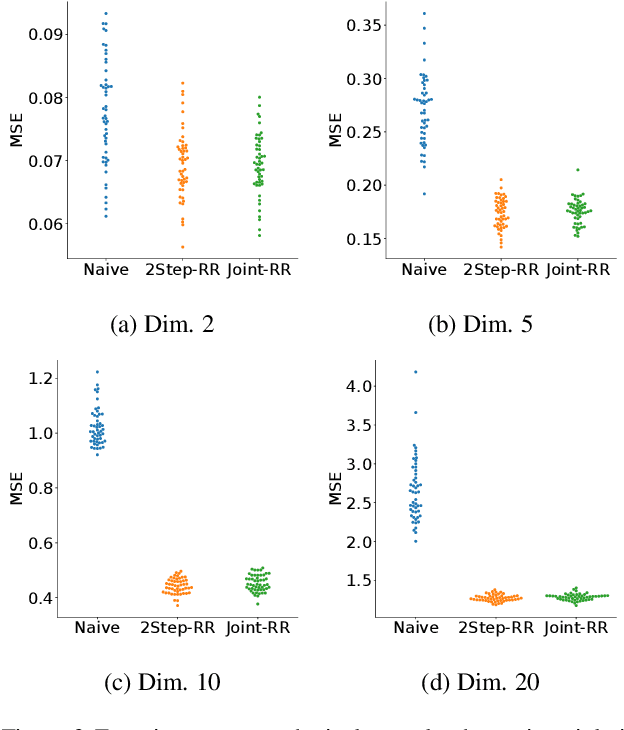
A default assumption in many machine learning scenarios is that the training and test samples are drawn from the same probability distribution. However, such an assumption is often violated in the real world due to non-stationarity of the environment or bias in sample selection. In this work, we consider a prevalent setting called covariate shift, where the input distribution differs between the training and test stages while the conditional distribution of the output given the input remains unchanged. Most of the existing methods for covariate shift adaptation are two-step approaches, which first calculate the importance weights and then conduct importance-weighted empirical risk minimization. In this paper, we propose a novel one-step approach that jointly learns the predictive model and the associated weights in one optimization by minimizing an upper bound of the test risk. We theoretically analyze the proposed method and provide a generalization error bound. We also empirically demonstrate the effectiveness of the proposed method.

Do We Need Zero Training Loss After Achieving Zero Training Error?

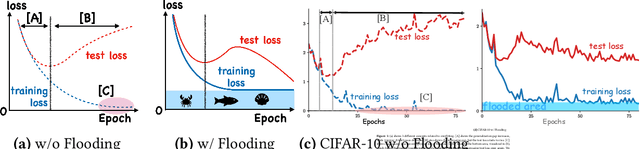
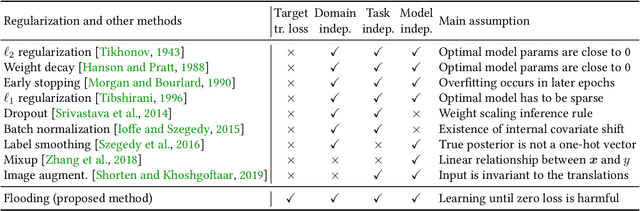
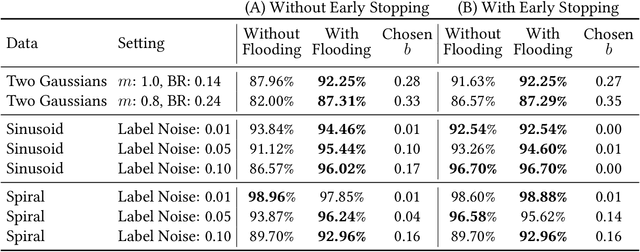
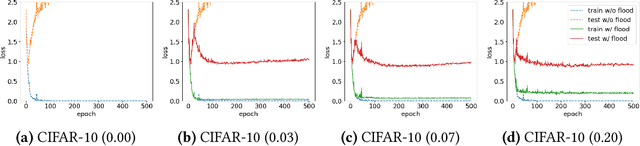
Overparameterized deep networks have the capacity to memorize training data with zero training error. Even after memorization, the training loss continues to approach zero, making the model overconfident and the test performance degraded. Since existing regularizers do not directly aim to avoid zero training loss, they often fail to maintain a moderate level of training loss, ending up with a too small or too large loss. We propose a direct solution called flooding that intentionally prevents further reduction of the training loss when it reaches a reasonably small value, which we call the flooding level. Our approach makes the loss float around the flooding level by doing mini-batched gradient descent as usual but gradient ascent if the training loss is below the flooding level. This can be implemented with one line of code, and is compatible with any stochastic optimizer and other regularizers. With flooding, the model will continue to "random walk" with the same non-zero training loss, and we expect it to drift into an area with a flat loss landscape that leads to better generalization. We experimentally show that flooding improves performance and as a byproduct, induces a double descent curve of the test loss.

Uplift Modeling from Separate Labels

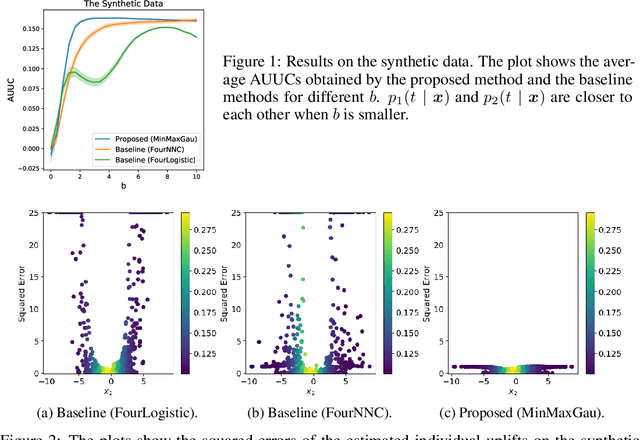
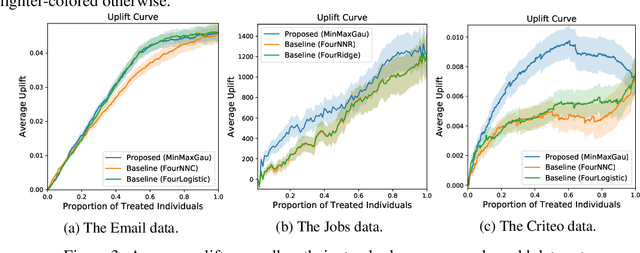
Uplift modeling is aimed at estimating the incremental impact of an action on an individual's behavior, which is useful in various application domains such as targeted marketing (advertisement campaigns) and personalized medicine (medical treatments). Conventional methods of uplift modeling require every instance to be jointly equipped with two types of labels: the taken action and its outcome. However, obtaining two labels for each instance at the same time is difficult or expensive in many real-world problems. In this paper, we propose a novel method of uplift modeling that is applicable to a more practical setting where only one type of labels is available for each instance. We show a generalization error bound for the proposed method and demonstrate its effectiveness through experiments.

Regularized Multi-Task Learning for Multi-Dimensional Log-Density Gradient Estimation

Log-density gradient estimation is a fundamental statistical problem and possesses various practical applications such as clustering and measuring non-Gaussianity. A naive two-step approach of first estimating the density and then taking its log-gradient is unreliable because an accurate density estimate does not necessarily lead to an accurate log-density gradient estimate. To cope with this problem, a method to directly estimate the log-density gradient without density estimation has been explored, and demonstrated to work much better than the two-step method. The objective of this paper is to further improve the performance of this direct method in multi-dimensional cases. Our idea is to regard the problem of log-density gradient estimation in each dimension as a task, and apply regularized multi-task learning to the direct log-density gradient estimator. We experimentally demonstrate the usefulness of the proposed multi-task method in log-density gradient estimation and mode-seeking clustering.