Towards Reliable and Explainable AI Model for Solid Pulmonary Nodule Diagnosis

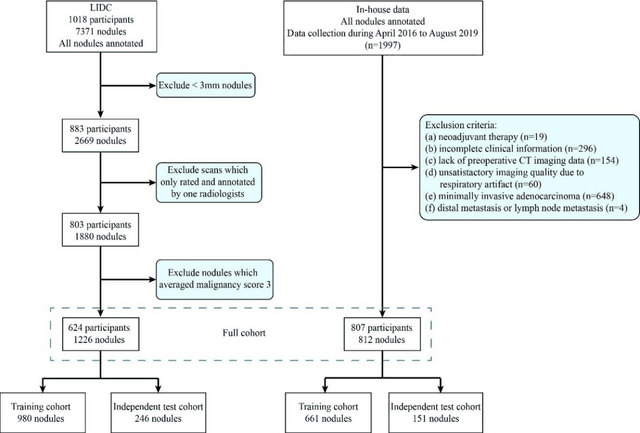
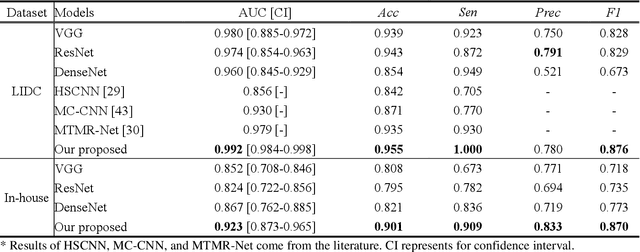
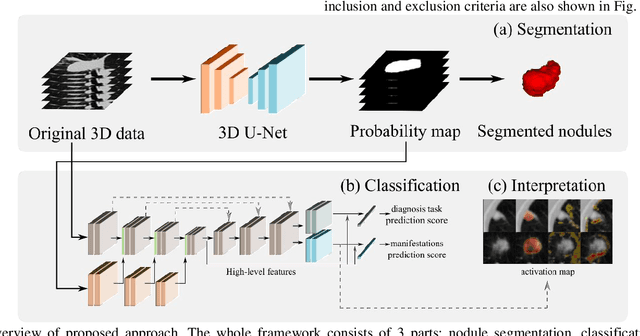
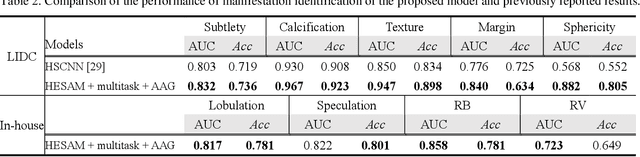
Lung cancer has the highest mortality rate of deadly cancers in the world. Early detection is essential to treatment of lung cancer. However, detection and accurate diagnosis of pulmonary nodules depend heavily on the experiences of radiologists and can be a heavy workload for them. Computer-aided diagnosis (CAD) systems have been developed to assist radiologists in nodule detection and diagnosis, greatly easing the workload while increasing diagnosis accuracy. Recent development of deep learning, greatly improved the performance of CAD systems. However, lack of model reliability and interpretability remains a major obstacle for its large-scale clinical application. In this work, we proposed a multi-task explainable deep-learning model for pulmonary nodule diagnosis. Our neural model can not only predict lesion malignancy but also identify relevant manifestations. Further, the location of each manifestation can also be visualized for visual interpretability. Our proposed neural model achieved a test AUC of 0.992 on LIDC public dataset and a test AUC of 0.923 on our in-house dataset. Moreover, our experimental results proved that by incorporating manifestation identification tasks into the multi-task model, the accuracy of the malignancy classification can also be improved. This multi-task explainable model may provide a scheme for better interaction with the radiologists in a clinical environment.

Fast sensor placement by enlarging principle submatrix for large-scale linear inverse problems

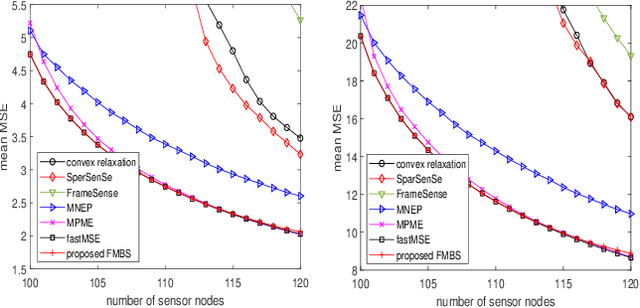
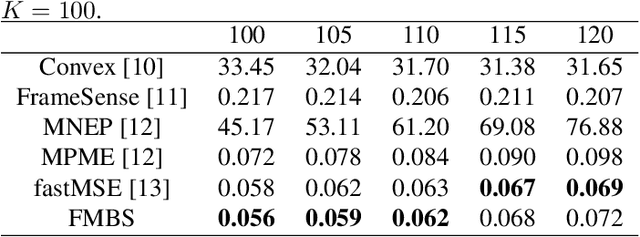
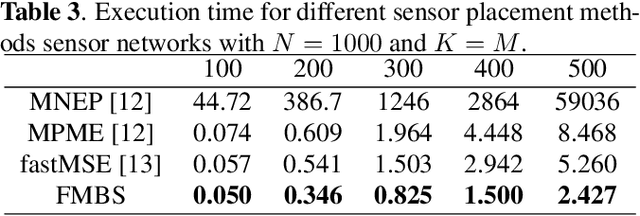
Sensor placement for linear inverse problems is the selection of locations to assign sensors so that the entire physical signal can be well recovered from partial observations. In this paper, we propose a fast sampling algorithm to place sensors. Specifically, assuming that the field signal $\mathbf{f}$ is represented by a linear model $\mathbf{f}=\pmb{\phi}\mathbf{g}$, it can be estimated from partial noisy samples via an unbiased least-squares (LS) method, whose expected mean square error (MSE) depends on chosen samples. First, we formulate an approximate MSE problem, and then prove it is equivalent to a problem related to a principle submatrix of $\pmb{\phi}\pmb{\phi}^\top$ indexed by sample set. To solve the formulated problem, we devise a fast greedy algorithm with simple matrix-vector multiplications, leveraging a matrix inverse formula. To further reduce complexity, we reuse results in the previous greedy step for warm start, so that candidates can be evaluated via lightweight vector-vector multiplications. Extensive experiments show that our proposed sensor placement method achieved the lowest sensor sampling time and the best performance compared to state-of-the-art schemes.

Learning Sparse Graph Laplacian with $K$ Eigenvector Prior via Iterative GLASSO and Projection

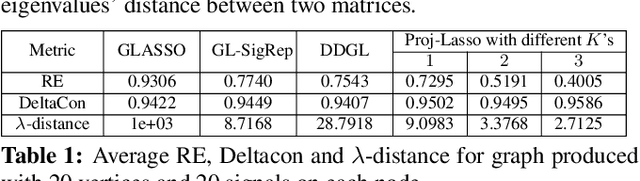
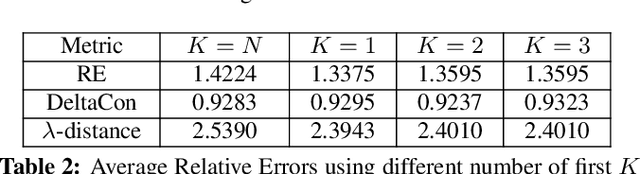
Learning a suitable graph is an important precursor to many graph signal processing (GSP) pipelines, such as graph spectral signal compression and denoising. Previous graph learning algorithms either i) make some assumptions on connectivity (e.g., graph sparsity), or ii) make simple graph edge assumptions such as positive edges only. In this paper, given an empirical covariance matrix $\bar{C}$ computed from data as input, we consider a structural assumption on the graph Laplacian matrix $L$: the first $K$ eigenvectors of $L$ are pre-selected, e.g., based on domain-specific criteria, such as computation requirement, and the remaining eigenvectors are then learned from data. One example use case is image coding, where the first eigenvector is pre-chosen to be constant, regardless of available observed data. We first prove that the subspace of symmetric positive semi-definite (PSD) matrices $H_{u}^+$ with the first $K$ eigenvectors being $\{u_k\}$ in a defined Hilbert space is a convex cone. We then construct an operator to project a given positive definite (PD) matrix $L$ to $H_{u}^+$, inspired by the Gram-Schmidt procedure. Finally, we design an efficient hybrid graphical lasso/projection algorithm to compute the most suitable graph Laplacian matrix $L^* \in H_{u}^+$ given $\bar{C}$. Experimental results show that given the first $K$ eigenvectors as a prior, our algorithm outperforms competing graph learning schemes using a variety of graph comparison metrics.