Fast sensor placement by enlarging principle submatrix for large-scale linear inverse problems
Paper and Code
Oct 07, 2021
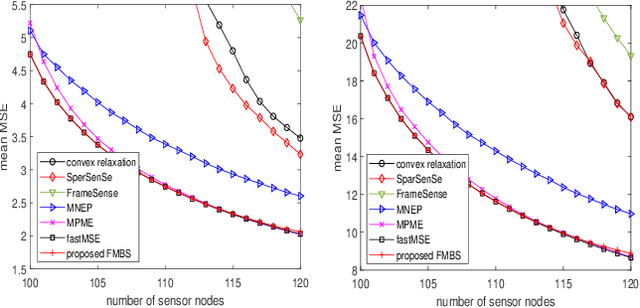
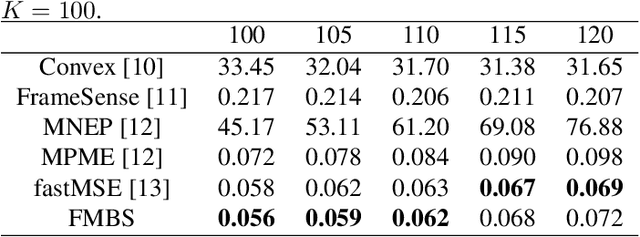
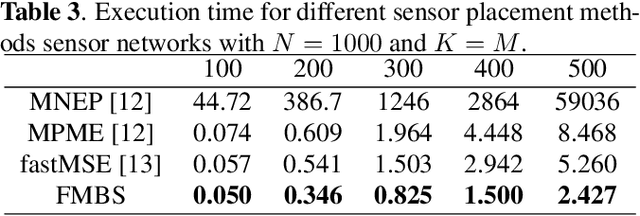
Sensor placement for linear inverse problems is the selection of locations to assign sensors so that the entire physical signal can be well recovered from partial observations. In this paper, we propose a fast sampling algorithm to place sensors. Specifically, assuming that the field signal $\mathbf{f}$ is represented by a linear model $\mathbf{f}=\pmb{\phi}\mathbf{g}$, it can be estimated from partial noisy samples via an unbiased least-squares (LS) method, whose expected mean square error (MSE) depends on chosen samples. First, we formulate an approximate MSE problem, and then prove it is equivalent to a problem related to a principle submatrix of $\pmb{\phi}\pmb{\phi}^\top$ indexed by sample set. To solve the formulated problem, we devise a fast greedy algorithm with simple matrix-vector multiplications, leveraging a matrix inverse formula. To further reduce complexity, we reuse results in the previous greedy step for warm start, so that candidates can be evaluated via lightweight vector-vector multiplications. Extensive experiments show that our proposed sensor placement method achieved the lowest sensor sampling time and the best performance compared to state-of-the-art schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge