The Power of Preconditioning in Overparameterized Low-Rank Matrix Sensing

We propose $\textsf{ScaledGD($\lambda$)}$, a preconditioned gradient descent method to tackle the low-rank matrix sensing problem when the true rank is unknown, and when the matrix is possibly ill-conditioned. Using overparametrized factor representations, $\textsf{ScaledGD($\lambda$)}$ starts from a small random initialization, and proceeds by gradient descent with a specific form of damped preconditioning to combat bad curvatures induced by overparameterization and ill-conditioning. At the expense of light computational overhead incurred by preconditioners, $\textsf{ScaledGD($\lambda$)}$ is remarkably robust to ill-conditioning compared to vanilla gradient descent ($\textsf{GD}$) even with overprameterization. Specifically, we show that, under the Gaussian design, $\textsf{ScaledGD($\lambda$)}$ converges to the true low-rank matrix at a constant linear rate after a small number of iterations that scales only logarithmically with respect to the condition number and the problem dimension. This significantly improves over the convergence rate of vanilla $\textsf{GD}$ which suffers from a polynomial dependency on the condition number. Our work provides evidence on the power of preconditioning in accelerating the convergence without hurting generalization in overparameterized learning.

Nonparametric mixture MLEs under Gaussian-smoothed optimal transport distance

The Gaussian-smoothed optimal transport (GOT) framework, pioneered in Goldfeld et al. (2020) and followed up by a series of subsequent papers, has quickly caught attention among researchers in statistics, machine learning, information theory, and related fields. One key observation made therein is that, by adapting to the GOT framework instead of its unsmoothed counterpart, the curse of dimensionality for using the empirical measure to approximate the true data generating distribution can be lifted. The current paper shows that a related observation applies to the estimation of nonparametric mixing distributions in discrete exponential family models, where under the GOT cost the estimation accuracy of the nonparametric MLE can be accelerated to a polynomial rate. This is in sharp contrast to the classical sub-polynomial rates based on unsmoothed metrics, which cannot be improved from an information-theoretical perspective. A key step in our analysis is the establishment of a new Jackson-type approximation bound of Gaussian-convoluted Lipschitz functions. This insight bridges existing techniques of analyzing the nonparametric MLEs and the new GOT framework.

Uncertainty quantification in the Bradley-Terry-Luce model

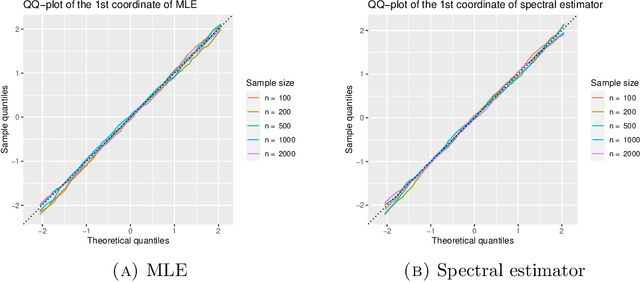
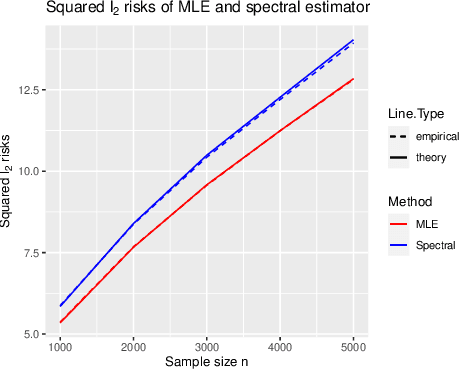
The Bradley-Terry-Luce (BTL) model is a benchmark model for pairwise comparisons between individuals. Despite recent progress on the first-order asymptotics of several popular procedures, the understanding of uncertainty quantification in the BTL model remains largely incomplete, especially when the underlying comparison graph is sparse. In this paper, we fill this gap by focusing on two estimators that have received much recent attention: the maximum likelihood estimator (MLE) and the spectral estimator. Using a unified proof strategy, we derive sharp and uniform non-asymptotic expansions for both estimators in the sparsest possible regime (up to some poly-logarithmic factors) of the underlying comparison graph. These expansions allow us to obtain: (i) finite-dimensional central limit theorems for both estimators; (ii) construction of confidence intervals for individual ranks; (iii) optimal constant of $\ell_2$ estimation, which is achieved by the MLE but not by the spectral estimator. Our proof is based on a self-consistent equation of the second-order remainder vector and a novel leave-two-out analysis.