High-dimensional Location Estimation via Norm Concentration for Subgamma Vectors

In location estimation, we are given $n$ samples from a known distribution $f$ shifted by an unknown translation $\lambda$, and want to estimate $\lambda$ as precisely as possible. Asymptotically, the maximum likelihood estimate achieves the Cram\'er-Rao bound of error $\mathcal N(0, \frac{1}{n\mathcal I})$, where $\mathcal I$ is the Fisher information of $f$. However, the $n$ required for convergence depends on $f$, and may be arbitrarily large. We build on the theory using \emph{smoothed} estimators to bound the error for finite $n$ in terms of $\mathcal I_r$, the Fisher information of the $r$-smoothed distribution. As $n \to \infty$, $r \to 0$ at an explicit rate and this converges to the Cram\'er-Rao bound. We (1) improve the prior work for 1-dimensional $f$ to converge for constant failure probability in addition to high probability, and (2) extend the theory to high-dimensional distributions. In the process, we prove a new bound on the norm of a high-dimensional random variable whose 1-dimensional projections are subgamma, which may be of independent interest.

Perception-driven Formation Control of Airships

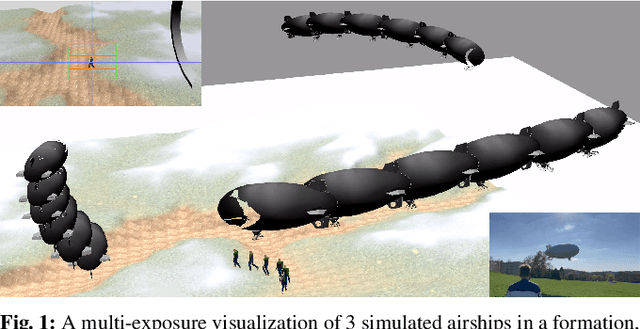
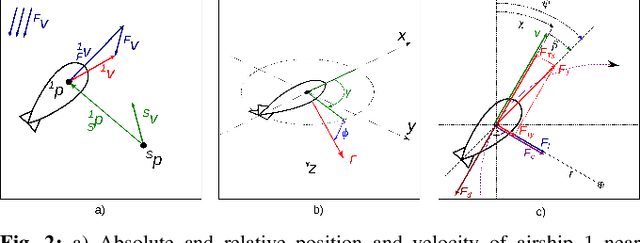
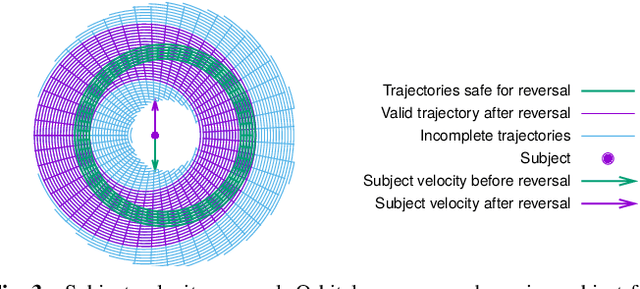
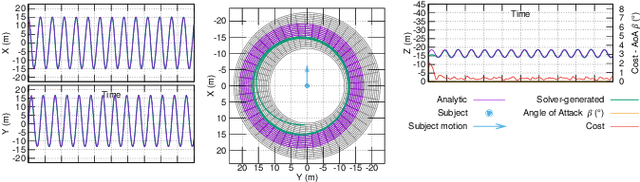
For tracking and motion capture (MoCap) of animals in their natural habitat, a formation of safe and silent aerial platforms, such as airships with on-board cameras, is well suited. However, unlike multi-rotors, airships are severely motion constrained and affected by ambient wind. Their orientation and flight direction are also tightly coupled. Therefore, state-of-the-art MPC-based formation control methods for perception tasks are not directly applicable for a team of airships. In this paper, we address this problem by first exploiting a periodic relationship between the airspeed of an airship and its distance to the subject. We use it to derive analytical and numeric solutions that satisfy the MoCap perception constraints. Based on this, we develop an MPC-based formation controller. We performed detailed analysis of our solution, including the effects of changing physical parameters (like angle of attack and pitch angle) on it. Extensive simulation experiments, comparing results for different formation sizes, different wind conditions and various subject speeds, are presented. A demonstration of our method on a real airship is also included. We have released all of our source code at https://github.com/robot-perception-group/Airship-MPC. A video describing our approach and results can be watched at https://youtu.be/ihS0_VRD_kk

Hardness and Algorithms for Robust and Sparse Optimization

We explore algorithms and limitations for sparse optimization problems such as sparse linear regression and robust linear regression. The goal of the sparse linear regression problem is to identify a small number of key features, while the goal of the robust linear regression problem is to identify a small number of erroneous measurements. Specifically, the sparse linear regression problem seeks a $k$-sparse vector $x\in\mathbb{R}^d$ to minimize $\|Ax-b\|_2$, given an input matrix $A\in\mathbb{R}^{n\times d}$ and a target vector $b\in\mathbb{R}^n$, while the robust linear regression problem seeks a set $S$ that ignores at most $k$ rows and a vector $x$ to minimize $\|(Ax-b)_S\|_2$. We first show bicriteria, NP-hardness of approximation for robust regression building on the work of [OWZ15] which implies a similar result for sparse regression. We further show fine-grained hardness of robust regression through a reduction from the minimum-weight $k$-clique conjecture. On the positive side, we give an algorithm for robust regression that achieves arbitrarily accurate additive error and uses runtime that closely matches the lower bound from the fine-grained hardness result, as well as an algorithm for sparse regression with similar runtime. Both our upper and lower bounds rely on a general reduction from robust linear regression to sparse regression that we introduce. Our algorithms, inspired by the 3SUM problem, use approximate nearest neighbor data structures and may be of independent interest for solving sparse optimization problems. For instance, we demonstrate that our techniques can also be used for the well-studied sparse PCA problem.

Sharp Constants in Uniformity Testing via the Huber Statistic

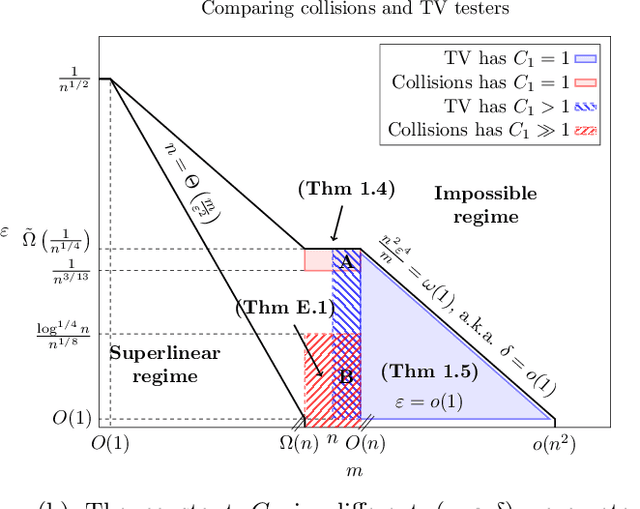
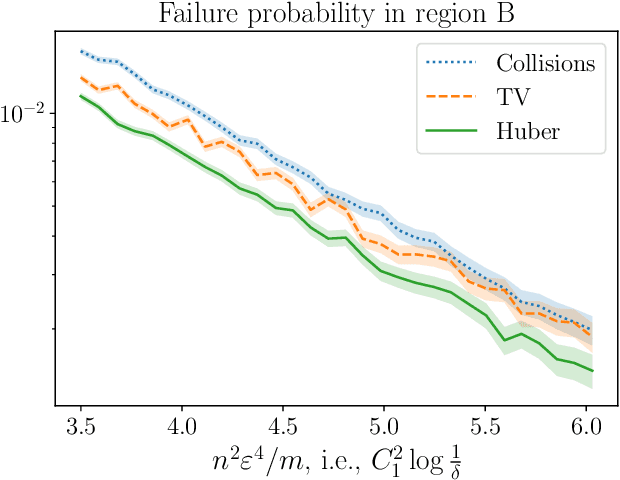
Uniformity testing is one of the most well-studied problems in property testing, with many known test statistics, including ones based on counting collisions, singletons, and the empirical TV distance. It is known that the optimal sample complexity to distinguish the uniform distribution on $m$ elements from any $\epsilon$-far distribution with $1-\delta$ probability is $n = \Theta\left(\frac{\sqrt{m \log (1/\delta)}}{\epsilon^2} + \frac{\log (1/\delta)}{\epsilon^2}\right)$, which is achieved by the empirical TV tester. Yet in simulation, these theoretical analyses are misleading: in many cases, they do not correctly rank order the performance of existing testers, even in an asymptotic regime of all parameters tending to $0$ or $\infty$. We explain this discrepancy by studying the \emph{constant factors} required by the algorithms. We show that the collisions tester achieves a sharp maximal constant in the number of standard deviations of separation between uniform and non-uniform inputs. We then introduce a new tester based on the Huber loss, and show that it not only matches this separation, but also has tails corresponding to a Gaussian with this separation. This leads to a sample complexity of $(1 + o(1))\frac{\sqrt{m \log (1/\delta)}}{\epsilon^2}$ in the regime where this term is dominant, unlike all other existing testers.

Finite-Sample Maximum Likelihood Estimation of Location

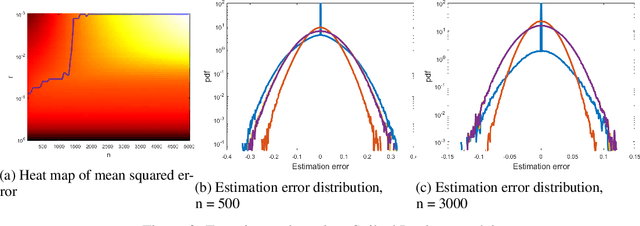
We consider 1-dimensional location estimation, where we estimate a parameter $\lambda$ from $n$ samples $\lambda + \eta_i$, with each $\eta_i$ drawn i.i.d. from a known distribution $f$. For fixed $f$ the maximum-likelihood estimate (MLE) is well-known to be optimal in the limit as $n \to \infty$: it is asymptotically normal with variance matching the Cram\'er-Rao lower bound of $\frac{1}{n\mathcal{I}}$, where $\mathcal{I}$ is the Fisher information of $f$. However, this bound does not hold for finite $n$, or when $f$ varies with $n$. We show for arbitrary $f$ and $n$ that one can recover a similar theory based on the Fisher information of a smoothed version of $f$, where the smoothing radius decays with $n$.

Deep Residual Reinforcement Learning based Autonomous Blimp Control

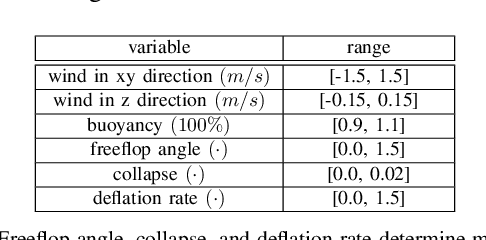
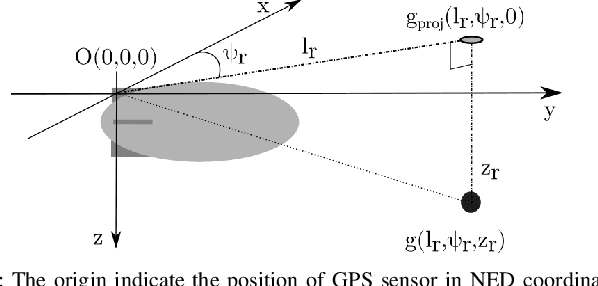
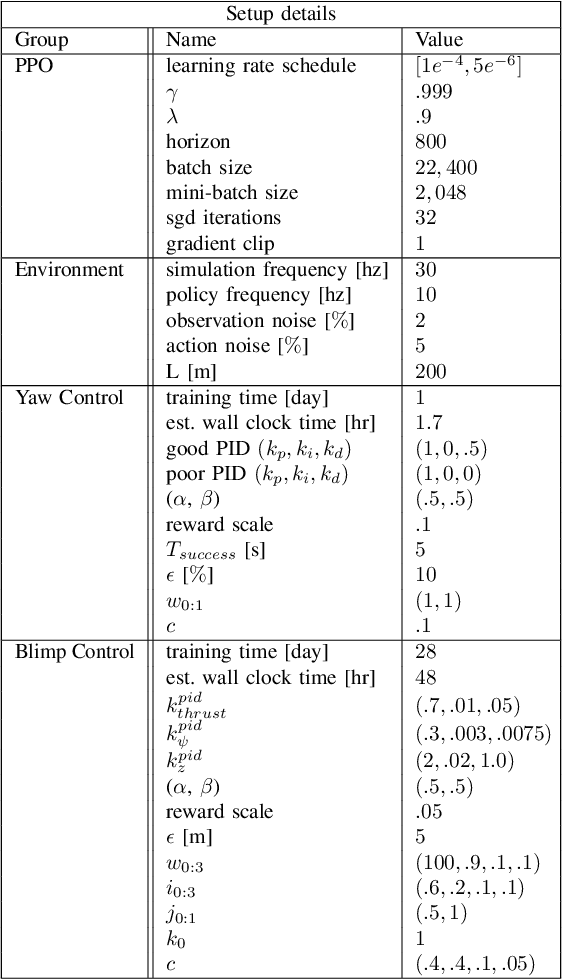
Blimps are well suited to perform long-duration aerial tasks as they are energy efficient, relatively silent and safe. To address the blimp navigation and control task, in previous work we developed a hardware and software-in-the-loop framework and a PID-based controller for large blimps in the presence of wind disturbance. However, blimps have a deformable structure and their dynamics are inherently non-linear and time-delayed, making PID controllers difficult to tune. Thus, often resulting in large tracking errors. Moreover, the buoyancy of a blimp is constantly changing due to variations in ambient temperature and pressure. To address these issues, in this paper we present a learning-based framework based on deep residual reinforcement learning (DRRL), for the blimp control task. Within this framework, we first employ a PID controller to provide baseline performance. Subsequently, the DRRL agent learns to modify the PID decisions by interaction with the environment. We demonstrate in simulation that DRRL agent consistently improves the PID performance. Through rigorous simulation experiments, we show that the agent is robust to changes in wind speed and buoyancy. In real-world experiments, we demonstrate that the agent, trained only in simulation, is sufficiently robust to control an actual blimp in windy conditions. We openly provide the source code of our approach at https://github.com/ robot-perception-group/AutonomousBlimpDRL.

Coresets for Data Discretization and Sine Wave Fitting

In the \emph{monitoring} problem, the input is an unbounded stream $P={p_1,p_2\cdots}$ of integers in $[N]:=\{1,\cdots,N\}$, that are obtained from a sensor (such as GPS or heart beats of a human). The goal (e.g., for anomaly detection) is to approximate the $n$ points received so far in $P$ by a single frequency $\sin$, e.g. $\min_{c\in C}cost(P,c)+\lambda(c)$, where $cost(P,c)=\sum_{i=1}^n \sin^2(\frac{2\pi}{N} p_ic)$, $C\subseteq [N]$ is a feasible set of solutions, and $\lambda$ is a given regularization function. For any approximation error $\varepsilon>0$, we prove that \emph{every} set $P$ of $n$ integers has a weighted subset $S\subseteq P$ (sometimes called core-set) of cardinality $|S|\in O(\log(N)^{O(1)})$ that approximates $cost(P,c)$ (for every $c\in [N]$) up to a multiplicative factor of $1\pm\varepsilon$. Using known coreset techniques, this implies streaming algorithms using only $O((\log(N)\log(n))^{O(1)})$ memory. Our results hold for a large family of functions. Experimental results and open source code are provided.

AirPose: Multi-View Fusion Network for Aerial 3D Human Pose and Shape Estimation

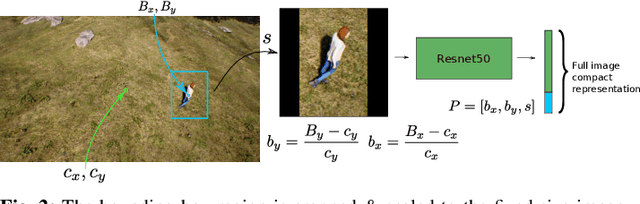
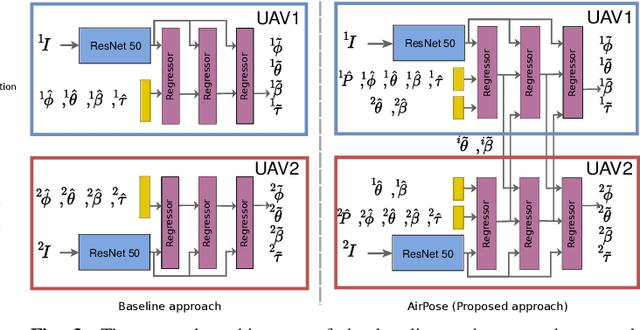
In this letter, we present a novel markerless 3D human motion capture (MoCap) system for unstructured, outdoor environments that uses a team of autonomous unmanned aerial vehicles (UAVs) with on-board RGB cameras and computation. Existing methods are limited by calibrated cameras and off-line processing. Thus, we present the first method (AirPose) to estimate human pose and shape using images captured by multiple extrinsically uncalibrated flying cameras. AirPose itself calibrates the cameras relative to the person instead of relying on any pre-calibration. It uses distributed neural networks running on each UAV that communicate viewpoint-independent information with each other about the person (i.e., their 3D shape and articulated pose). The person's shape and pose are parameterized using the SMPL-X body model, resulting in a compact representation, that minimizes communication between the UAVs. The network is trained using synthetic images of realistic virtual environments, and fine-tuned on a small set of real images. We also introduce an optimization-based post-processing method (AirPose$^{+}$) for offline applications that require higher MoCap quality. We make our method's code and data available for research at https://github.com/robot-perception-group/AirPose. A video describing the approach and results is available at https://youtu.be/xLYe1TNHsfs.

Autonomous Blimp Control using Deep Reinforcement Learning

Aerial robot solutions are becoming ubiquitous for an increasing number of tasks. Among the various types of aerial robots, blimps are very well suited to perform long-duration tasks while being energy efficient, relatively silent and safe. To address the blimp navigation and control task, in our recent work, we have developed a software-in-the-loop simulation and a PID-based controller for large blimps in the presence of wind disturbance. However, blimps have a deformable structure and their dynamics are inherently non-linear and time-delayed, often resulting in large trajectory tracking errors. Moreover, the buoyancy of a blimp is constantly changing due to changes in the ambient temperature and pressure. In the present paper, we explore a deep reinforcement learning (DRL) approach to address these issues. We train only in simulation, while keeping conditions as close as possible to the real-world scenario. We derive a compact state representation to reduce the training time and a discrete action space to enforce control smoothness. Our initial results in simulation show a significant potential of DRL in solving the blimp control task and robustness against moderate wind and parameter uncertainty. Extensive experiments are presented to study the robustness of our approach. We also openly provide the source code of our approach.

Robust Compressed Sensing MRI with Deep Generative Priors

The CSGM framework (Bora-Jalal-Price-Dimakis'17) has shown that deep generative priors can be powerful tools for solving inverse problems. However, to date this framework has been empirically successful only on certain datasets (for example, human faces and MNIST digits), and it is known to perform poorly on out-of-distribution samples. In this paper, we present the first successful application of the CSGM framework on clinical MRI data. We train a generative prior on brain scans from the fastMRI dataset, and show that posterior sampling via Langevin dynamics achieves high quality reconstructions. Furthermore, our experiments and theory show that posterior sampling is robust to changes in the ground-truth distribution and measurement process. Our code and models are available at: \url{https://github.com/utcsilab/csgm-mri-langevin}.