Provable Imbalanced Point Clustering

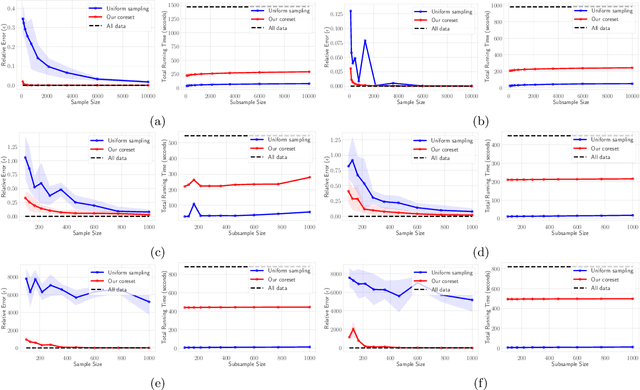
We suggest efficient and provable methods to compute an approximation for imbalanced point clustering, that is, fitting $k$-centers to a set of points in $\mathbb{R}^d$, for any $d,k\geq 1$. To this end, we utilize \emph{coresets}, which, in the context of the paper, are essentially weighted sets of points in $\mathbb{R}^d$ that approximate the fitting loss for every model in a given set, up to a multiplicative factor of $1\pm\varepsilon$. We provide [Section 3 and Section E in the appendix] experiments that show the empirical contribution of our suggested methods for real images (novel and reference), synthetic data, and real-world data. We also propose choice clustering, which by combining clustering algorithms yields better performance than each one separately.

ORBSLAM3-Enhanced Autonomous Toy Drones: Pioneering Indoor Exploration

Navigating toy drones through uncharted GPS-denied indoor spaces poses significant difficulties due to their reliance on GPS for location determination. In such circumstances, the necessity for achieving proper navigation is a primary concern. In response to this formidable challenge, we introduce a real-time autonomous indoor exploration system tailored for drones equipped with a monocular \emph{RGB} camera. Our system utilizes \emph{ORB-SLAM3}, a state-of-the-art vision feature-based SLAM, to handle both the localization of toy drones and the mapping of unmapped indoor terrains. Aside from the practicability of \emph{ORB-SLAM3}, the generated maps are represented as sparse point clouds, making them prone to the presence of outlier data. To address this challenge, we propose an outlier removal algorithm with provable guarantees. Furthermore, our system incorporates a novel exit detection algorithm, ensuring continuous exploration by the toy drone throughout the unfamiliar indoor environment. We also transform the sparse point to ensure proper path planning using existing path planners. To validate the efficacy and efficiency of our proposed system, we conducted offline and real-time experiments on the autonomous exploration of indoor spaces. The results from these endeavors demonstrate the effectiveness of our methods.

Provable Data Subset Selection For Efficient Neural Network Training

Radial basis function neural networks (\emph{RBFNN}) are {well-known} for their capability to approximate any continuous function on a closed bounded set with arbitrary precision given enough hidden neurons. In this paper, we introduce the first algorithm to construct coresets for \emph{RBFNNs}, i.e., small weighted subsets that approximate the loss of the input data on any radial basis function network and thus approximate any function defined by an \emph{RBFNN} on the larger input data. In particular, we construct coresets for radial basis and Laplacian loss functions. We then use our coresets to obtain a provable data subset selection algorithm for training deep neural networks. Since our coresets approximate every function, they also approximate the gradient of each weight in a neural network, which is a particular function on the input. We then perform empirical evaluations on function approximation and dataset subset selection on popular network architectures and data sets, demonstrating the efficacy and accuracy of our coreset construction.

Deep Learning on Home Drone: Searching for the Optimal Architecture

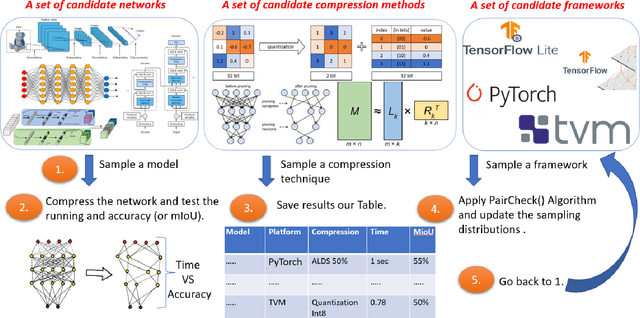
We suggest the first system that runs real-time semantic segmentation via deep learning on a weak micro-computer such as the Raspberry Pi Zero v2 (whose price was \$15) attached to a toy-drone. In particular, since the Raspberry Pi weighs less than $16$ grams, and its size is half of a credit card, we could easily attach it to the common commercial DJI Tello toy-drone (<\$100, <90 grams, 98 $\times$ 92.5 $\times$ 41 mm). The result is an autonomous drone (no laptop nor human in the loop) that can detect and classify objects in real-time from a video stream of an on-board monocular RGB camera (no GPS or LIDAR sensors). The companion videos demonstrate how this Tello drone scans the lab for people (e.g. for the use of firefighters or security forces) and for an empty parking slot outside the lab. Existing deep learning solutions are either much too slow for real-time computation on such IoT devices, or provide results of impractical quality. Our main challenge was to design a system that takes the best of all worlds among numerous combinations of networks, deep learning platforms/frameworks, compression techniques, and compression ratios. To this end, we provide an efficient searching algorithm that aims to find the optimal combination which results in the best tradeoff between the network running time and its accuracy/performance.

New Coresets for Projective Clustering and Applications

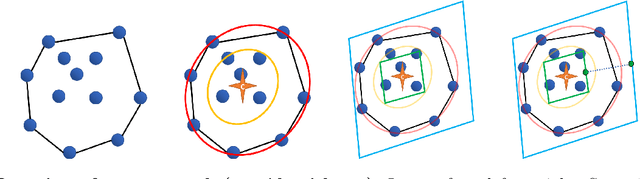
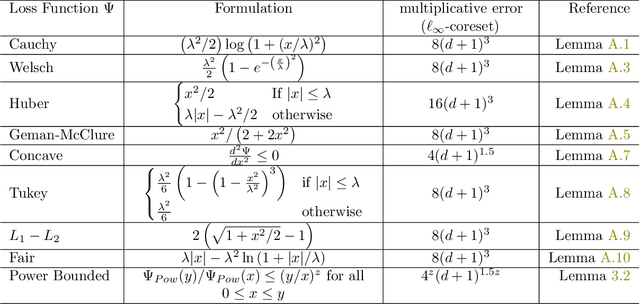
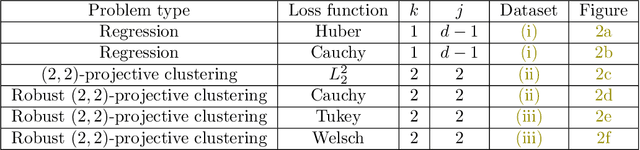
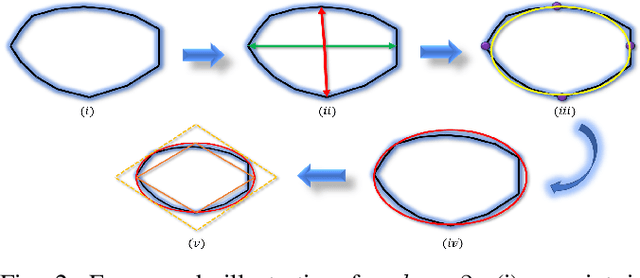
$(j,k)$-projective clustering is the natural generalization of the family of $k$-clustering and $j$-subspace clustering problems. Given a set of points $P$ in $\mathbb{R}^d$, the goal is to find $k$ flats of dimension $j$, i.e., affine subspaces, that best fit $P$ under a given distance measure. In this paper, we propose the first algorithm that returns an $L_\infty$ coreset of size polynomial in $d$. Moreover, we give the first strong coreset construction for general $M$-estimator regression. Specifically, we show that our construction provides efficient coreset constructions for Cauchy, Welsch, Huber, Geman-McClure, Tukey, $L_1-L_2$, and Fair regression, as well as general concave and power-bounded loss functions. Finally, we provide experimental results based on real-world datasets, showing the efficacy of our approach.

Obstacle Aware Sampling for Path Planning

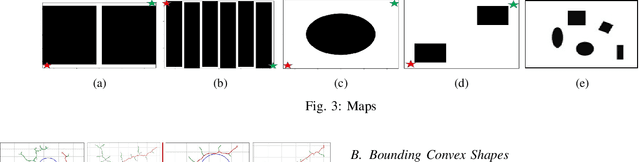
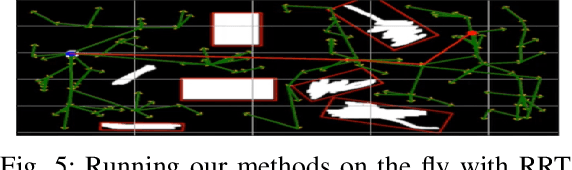
Many path planning algorithms are based on sampling the state space. While this approach is very simple, it can become costly when the obstacles are unknown, since samples hitting these obstacles are wasted. The goal of this paper is to efficiently identify obstacles in a map and remove them from the sampling space. To this end, we propose a pre-processing algorithm for space exploration that enables more efficient sampling. We show that it can boost the performance of other space sampling methods and path planners. Our approach is based on the fact that a convex obstacle can be approximated provably well by its minimum volume enclosing ellipsoid (MVEE), and a non-convex obstacle may be partitioned into convex shapes. Our main contribution is an algorithm that strategically finds a small sample, called the \emph{active-coreset}, that adaptively samples the space via membership-oracle such that the MVEE of the coreset approximates the MVEE of the obstacle. Experimental results confirm the effectiveness of our approach across multiple planners based on Rapidly-exploring random trees, showing significant improvement in terms of time and path length.

Coresets for Data Discretization and Sine Wave Fitting

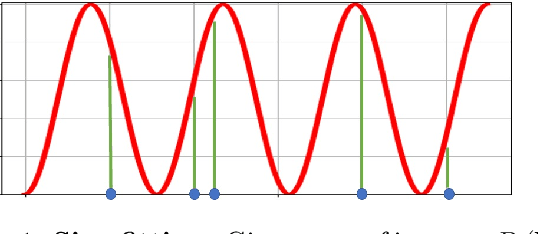
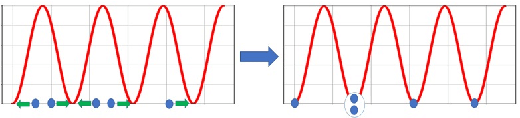
In the \emph{monitoring} problem, the input is an unbounded stream $P={p_1,p_2\cdots}$ of integers in $[N]:=\{1,\cdots,N\}$, that are obtained from a sensor (such as GPS or heart beats of a human). The goal (e.g., for anomaly detection) is to approximate the $n$ points received so far in $P$ by a single frequency $\sin$, e.g. $\min_{c\in C}cost(P,c)+\lambda(c)$, where $cost(P,c)=\sum_{i=1}^n \sin^2(\frac{2\pi}{N} p_ic)$, $C\subseteq [N]$ is a feasible set of solutions, and $\lambda$ is a given regularization function. For any approximation error $\varepsilon>0$, we prove that \emph{every} set $P$ of $n$ integers has a weighted subset $S\subseteq P$ (sometimes called core-set) of cardinality $|S|\in O(\log(N)^{O(1)})$ that approximates $cost(P,c)$ (for every $c\in [N]$) up to a multiplicative factor of $1\pm\varepsilon$. Using known coreset techniques, this implies streaming algorithms using only $O((\log(N)\log(n))^{O(1)})$ memory. Our results hold for a large family of functions. Experimental results and open source code are provided.

Newton-PnP: Real-time Visual Navigation for Autonomous Toy-Drones

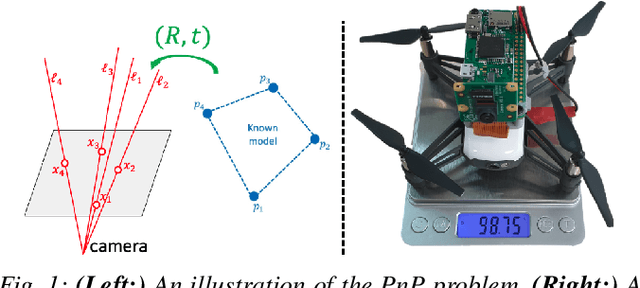
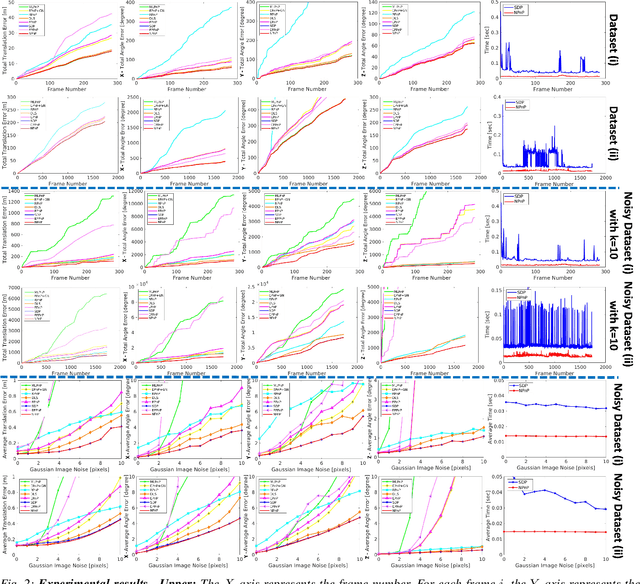
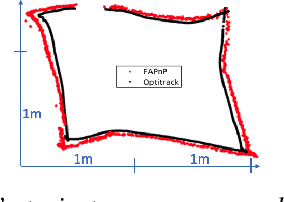
The Perspective-n-Point problem aims to estimate the relative pose between a calibrated monocular camera and a known 3D model, by aligning pairs of 2D captured image points to their corresponding 3D points in the model. We suggest an algorithm that runs on weak IoT devices in real-time but still provides provable theoretical guarantees for both running time and correctness. Existing solvers provide only one of these requirements. Our main motivation was to turn the popular DJI's Tello Drone (<90gr, <\$100) into an autonomous drone that navigates in an indoor environment with no external human/laptop/sensor, by simply attaching a Raspberry PI Zero (<9gr, <\$25) to it. This tiny micro-processor takes as input a real-time video from a tiny RGB camera, and runs our PnP solver on-board. Extensive experimental results, open source code, and a demonstration video are included.

Introduction to Coresets: Approximated Mean

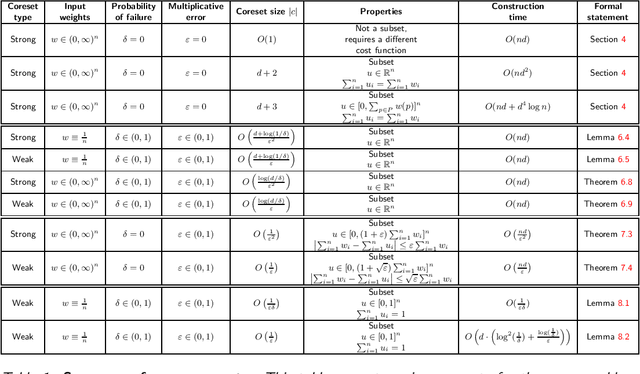
A \emph{strong coreset} for the mean queries of a set $P$ in ${\mathbb{R}}^d$ is a small weighted subset $C\subseteq P$, which provably approximates its sum of squared distances to any center (point) $x\in {\mathbb{R}}^d$. A \emph{weak coreset} is (also) a small weighted subset $C$ of $P$, whose mean approximates the mean of $P$. While computing the mean of $P$ can be easily computed in linear time, its coreset can be used to solve harder constrained version, and is in the heart of generalizations such as coresets for $k$-means clustering. In this paper, we survey most of the mean coreset construction techniques, and suggest a unified analysis methodology for providing and explaining classical and modern results including step-by-step proofs. In particular, we collected folklore and scattered related results, some of which are not formally stated elsewhere. Throughout this survey, we present, explain, and prove a set of techniques, reductions, and algorithms very widespread and crucial in this field. However, when put to use in the (relatively simple) mean problem, such techniques are much simpler to grasp. The survey may help guide new researchers unfamiliar with the field, and introduce them to the very basic foundations of coresets, through a simple, yet fundamental, problem. Experts in this area might appreciate the unified analysis flow, and the comparison table for existing results. Finally, to encourage and help practitioners and software engineers, we provide full open source code for all presented algorithms.

A Unified Approach to Coreset Learning

Coreset of a given dataset and loss function is usually a small weighed set that approximates this loss for every query from a given set of queries. Coresets have shown to be very useful in many applications. However, coresets construction is done in a problem dependent manner and it could take years to design and prove the correctness of a coreset for a specific family of queries. This could limit coresets use in practical applications. Moreover, small coresets provably do not exist for many problems. To address these limitations, we propose a generic, learning-based algorithm for construction of coresets. Our approach offers a new definition of coreset, which is a natural relaxation of the standard definition and aims at approximating the \emph{average} loss of the original data over the queries. This allows us to use a learning paradigm to compute a small coreset of a given set of inputs with respect to a given loss function using a training set of queries. We derive formal guarantees for the proposed approach. Experimental evaluation on deep networks and classic machine learning problems show that our learned coresets yield comparable or even better results than the existing algorithms with worst-case theoretical guarantees (that may be too pessimistic in practice). Furthermore, our approach applied to deep network pruning provides the first coreset for a full deep network, i.e., compresses all the network at once, and not layer by layer or similar divide-and-conquer methods.