On Learning Parallel Pancakes with Mostly Uniform Weights

We study the complexity of learning $k$-mixtures of Gaussians ($k$-GMMs) on $\mathbb{R}^d$. This task is known to have complexity $d^{\Omega(k)}$ in full generality. To circumvent this exponential lower bound on the number of components, research has focused on learning families of GMMs satisfying additional structural properties. A natural assumption posits that the component weights are not exponentially small and that the components have the same unknown covariance. Recent work gave a $d^{O(\log(1/w_{\min}))}$-time algorithm for this class of GMMs, where $w_{\min}$ is the minimum weight. Our first main result is a Statistical Query (SQ) lower bound showing that this quasi-polynomial upper bound is essentially best possible, even for the special case of uniform weights. Specifically, we show that it is SQ-hard to distinguish between such a mixture and the standard Gaussian. We further explore how the distribution of weights affects the complexity of this task. Our second main result is a quasi-polynomial upper bound for the aforementioned testing task when most of the weights are uniform while a small fraction of the weights are potentially arbitrary.

Clustering Mixtures of Bounded Covariance Distributions Under Optimal Separation

We study the clustering problem for mixtures of bounded covariance distributions, under a fine-grained separation assumption. Specifically, given samples from a $k$-component mixture distribution $D = \sum_{i =1}^k w_i P_i$, where each $w_i \ge \alpha$ for some known parameter $\alpha$, and each $P_i$ has unknown covariance $\Sigma_i \preceq \sigma^2_i \cdot I_d$ for some unknown $\sigma_i$, the goal is to cluster the samples assuming a pairwise mean separation in the order of $(\sigma_i+\sigma_j)/\sqrt{\alpha}$ between every pair of components $P_i$ and $P_j$. Our contributions are as follows: For the special case of nearly uniform mixtures, we give the first poly-time algorithm for this clustering task. Prior work either required separation scaling with the maximum cluster standard deviation (i.e. $\max_i \sigma_i$) [DKK+22b] or required both additional structural assumptions and mean separation scaling as a large degree polynomial in $1/\alpha$ [BKK22]. For general-weight mixtures, we point out that accurate clustering is information-theoretically impossible under our fine-grained mean separation assumptions. We introduce the notion of a clustering refinement -- a list of not-too-small subsets satisfying a similar separation, and which can be merged into a clustering approximating the ground truth -- and show that it is possible to efficiently compute an accurate clustering refinement of the samples. Furthermore, under a variant of the "no large sub-cluster'' condition from in prior work [BKK22], we show that our algorithm outputs an accurate clustering, not just a refinement, even for general-weight mixtures. As a corollary, we obtain efficient clustering algorithms for mixtures of well-conditioned high-dimensional log-concave distributions. Moreover, our algorithm is robust to $\Omega(\alpha)$-fraction of adversarial outliers.

Optimality in Mean Estimation: Beyond Worst-Case, Beyond Sub-Gaussian, and Beyond $1+α$ Moments

There is growing interest in improving our algorithmic understanding of fundamental statistical problems such as mean estimation, driven by the goal of understanding the limits of what we can extract from valuable data. The state of the art results for mean estimation in $\mathbb{R}$ are 1) the optimal sub-Gaussian mean estimator by [LV22], with the tight sub-Gaussian constant for all distributions with finite but unknown variance, and 2) the analysis of the median-of-means algorithm by [BCL13] and a lower bound by [DLLO16], characterizing the big-O optimal errors for distributions for which only a $1+\alpha$ moment exists for $\alpha \in (0,1)$. Both results, however, are optimal only in the worst case. We initiate the fine-grained study of the mean estimation problem: Can algorithms leverage useful features of the input distribution to beat the sub-Gaussian rate, without explicit knowledge of such features? We resolve this question with an unexpectedly nuanced answer: "Yes in limited regimes, but in general no". For any distribution $p$ with a finite mean, we construct a distribution $q$ whose mean is well-separated from $p$'s, yet $p$ and $q$ are not distinguishable with high probability, and $q$ further preserves $p$'s moments up to constants. The main consequence is that no reasonable estimator can asymptotically achieve better than the sub-Gaussian error rate for any distribution, matching the worst-case result of [LV22]. More generally, we introduce a new definitional framework to analyze the fine-grained optimality of algorithms, which we call "neighborhood optimality", interpolating between the unattainably strong "instance optimality" and the trivially weak "admissibility" definitions. Applying the new framework, we show that median-of-means is neighborhood optimal, up to constant factors. It is open to find a neighborhood-optimal estimator without constant factor slackness.

Two-Stage Predict+Optimize for Mixed Integer Linear Programs with Unknown Parameters in Constraints

Consider the setting of constrained optimization, with some parameters unknown at solving time and requiring prediction from relevant features. Predict+Optimize is a recent framework for end-to-end training supervised learning models for such predictions, incorporating information about the optimization problem in the training process in order to yield better predictions in terms of the quality of the predicted solution under the true parameters. Almost all prior works have focused on the special case where the unknowns appear only in the optimization objective and not the constraints. Hu et al.~proposed the first adaptation of Predict+Optimize to handle unknowns appearing in constraints, but the framework has somewhat ad-hoc elements, and they provided a training algorithm only for covering and packing linear programs. In this work, we give a new \emph{simpler} and \emph{more powerful} framework called \emph{Two-Stage Predict+Optimize}, which we believe should be the canonical framework for the Predict+Optimize setting. We also give a training algorithm usable for all mixed integer linear programs, vastly generalizing the applicability of the framework. Experimental results demonstrate the superior prediction performance of our training framework over all classical and state-of-the-art methods.

Finite-Sample Symmetric Mean Estimation with Fisher Information Rate

The mean of an unknown variance-$\sigma^2$ distribution $f$ can be estimated from $n$ samples with variance $\frac{\sigma^2}{n}$ and nearly corresponding subgaussian rate. When $f$ is known up to translation, this can be improved asymptotically to $\frac{1}{n\mathcal I}$, where $\mathcal I$ is the Fisher information of the distribution. Such an improvement is not possible for general unknown $f$, but [Stone, 1975] showed that this asymptotic convergence $\textit{is}$ possible if $f$ is $\textit{symmetric}$ about its mean. Stone's bound is asymptotic, however: the $n$ required for convergence depends in an unspecified way on the distribution $f$ and failure probability $\delta$. In this paper we give finite-sample guarantees for symmetric mean estimation in terms of Fisher information. For every $f, n, \delta$ with $n > \log \frac{1}{\delta}$, we get convergence close to a subgaussian with variance $\frac{1}{n \mathcal I_r}$, where $\mathcal I_r$ is the $r$-$\textit{smoothed}$ Fisher information with smoothing radius $r$ that decays polynomially in $n$. Such a bound essentially matches the finite-sample guarantees in the known-$f$ setting.

A Spectral Algorithm for List-Decodable Covariance Estimation in Relative Frobenius Norm

We study the problem of list-decodable Gaussian covariance estimation. Given a multiset $T$ of $n$ points in $\mathbb R^d$ such that an unknown $\alpha<1/2$ fraction of points in $T$ are i.i.d. samples from an unknown Gaussian $\mathcal{N}(\mu, \Sigma)$, the goal is to output a list of $O(1/\alpha)$ hypotheses at least one of which is close to $\Sigma$ in relative Frobenius norm. Our main result is a $\mathrm{poly}(d,1/\alpha)$ sample and time algorithm for this task that guarantees relative Frobenius norm error of $\mathrm{poly}(1/\alpha)$. Importantly, our algorithm relies purely on spectral techniques. As a corollary, we obtain an efficient spectral algorithm for robust partial clustering of Gaussian mixture models (GMMs) -- a key ingredient in the recent work of [BDJ+22] on robustly learning arbitrary GMMs. Combined with the other components of [BDJ+22], our new method yields the first Sum-of-Squares-free algorithm for robustly learning GMMs. At the technical level, we develop a novel multi-filtering method for list-decodable covariance estimation that may be useful in other settings.

Branch & Learn with Post-hoc Correction for Predict+Optimize with Unknown Parameters in Constraints

Combining machine learning and constrained optimization, Predict+Optimize tackles optimization problems containing parameters that are unknown at the time of solving. Prior works focus on cases with unknowns only in the objectives. A new framework was recently proposed to cater for unknowns also in constraints by introducing a loss function, called Post-hoc Regret, that takes into account the cost of correcting an unsatisfiable prediction. Since Post-hoc Regret is non-differentiable, the previous work computes only its approximation. While the notion of Post-hoc Regret is general, its specific implementation is applicable to only packing and covering linear programming problems. In this paper, we first show how to compute Post-hoc Regret exactly for any optimization problem solvable by a recursive algorithm satisfying simple conditions. Experimentation demonstrates substantial improvement in the quality of solutions as compared to the earlier approximation approach. Furthermore, we show experimentally the empirical behavior of different combinations of correction and penalty functions used in the Post-hoc Regret of the same benchmarks. Results provide insights for defining the appropriate Post-hoc Regret in different application scenarios.

High-dimensional Location Estimation via Norm Concentration for Subgamma Vectors

In location estimation, we are given $n$ samples from a known distribution $f$ shifted by an unknown translation $\lambda$, and want to estimate $\lambda$ as precisely as possible. Asymptotically, the maximum likelihood estimate achieves the Cram\'er-Rao bound of error $\mathcal N(0, \frac{1}{n\mathcal I})$, where $\mathcal I$ is the Fisher information of $f$. However, the $n$ required for convergence depends on $f$, and may be arbitrarily large. We build on the theory using \emph{smoothed} estimators to bound the error for finite $n$ in terms of $\mathcal I_r$, the Fisher information of the $r$-smoothed distribution. As $n \to \infty$, $r \to 0$ at an explicit rate and this converges to the Cram\'er-Rao bound. We (1) improve the prior work for 1-dimensional $f$ to converge for constant failure probability in addition to high probability, and (2) extend the theory to high-dimensional distributions. In the process, we prove a new bound on the norm of a high-dimensional random variable whose 1-dimensional projections are subgamma, which may be of independent interest.

Outlier-Robust Sparse Mean Estimation for Heavy-Tailed Distributions

We study the fundamental task of outlier-robust mean estimation for heavy-tailed distributions in the presence of sparsity. Specifically, given a small number of corrupted samples from a high-dimensional heavy-tailed distribution whose mean $\mu$ is guaranteed to be sparse, the goal is to efficiently compute a hypothesis that accurately approximates $\mu$ with high probability. Prior work had obtained efficient algorithms for robust sparse mean estimation of light-tailed distributions. In this work, we give the first sample-efficient and polynomial-time robust sparse mean estimator for heavy-tailed distributions under mild moment assumptions. Our algorithm achieves the optimal asymptotic error using a number of samples scaling logarithmically with the ambient dimension. Importantly, the sample complexity of our method is optimal as a function of the failure probability $\tau$, having an additive $\log(1/\tau)$ dependence. Our algorithm leverages the stability-based approach from the algorithmic robust statistics literature, with crucial (and necessary) adaptations required in our setting. Our analysis may be of independent interest, involving the delicate design of a (non-spectral) decomposition for positive semi-definite matrices satisfying certain sparsity properties.

Predict+Optimize for Packing and Covering LPs with Unknown Parameters in Constraints

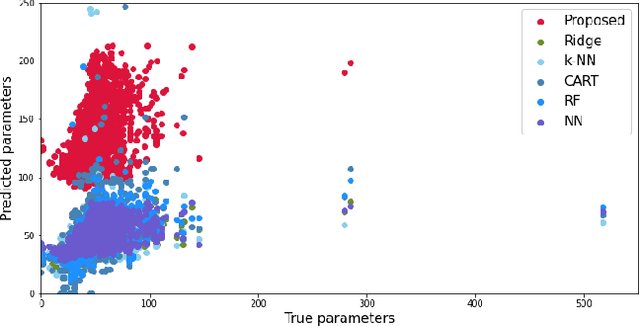
Predict+Optimize is a recently proposed framework which combines machine learning and constrained optimization, tackling optimization problems that contain parameters that are unknown at solving time. The goal is to predict the unknown parameters and use the estimates to solve for an estimated optimal solution to the optimization problem. However, all prior works have focused on the case where unknown parameters appear only in the optimization objective and not the constraints, for the simple reason that if the constraints were not known exactly, the estimated optimal solution might not even be feasible under the true parameters. The contributions of this paper are two-fold. First, we propose a novel and practically relevant framework for the Predict+Optimize setting, but with unknown parameters in both the objective and the constraints. We introduce the notion of a correction function, and an additional penalty term in the loss function, modelling practical scenarios where an estimated optimal solution can be modified into a feasible solution after the true parameters are revealed, but at an additional cost. Second, we propose a corresponding algorithmic approach for our framework, which handles all packing and covering linear programs. Our approach is inspired by the prior work of Mandi and Guns, though with crucial modifications and re-derivations for our very different setting. Experimentation demonstrates the superior empirical performance of our method over classical approaches.