Neural Differential Algebraic Equations

Differential-Algebraic Equations (DAEs) describe the temporal evolution of systems that obey both differential and algebraic constraints. Of particular interest are systems that contain implicit relationships between their components, such as conservation relationships. Here, we present Neural Differential-Algebraic Equations (NDAEs) suitable for data-driven modeling of DAEs. This methodology is built upon the concept of the Universal Differential Equation; that is, a model constructed as a system of Neural Ordinary Differential Equations informed by theory from particular science domains. In this work, we show that the proposed NDAEs abstraction is suitable for relevant system-theoretic data-driven modeling tasks. Presented examples include (i) the inverse problem of tank-manifold dynamics and (ii) discrepancy modeling of a network of pumps, tanks, and pipes. Our experiments demonstrate the proposed method's robustness to noise and extrapolation ability to (i) learn the behaviors of the system components and their interaction physics and (ii) disambiguate between data trends and mechanistic relationships contained in the system.

Domain-aware Control-oriented Neural Models for Autonomous Underwater Vehicles

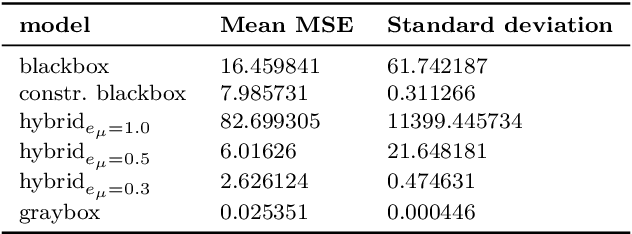
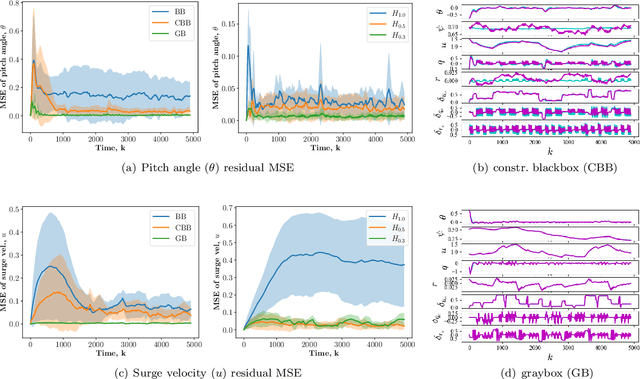
Conventional physics-based modeling is a time-consuming bottleneck in control design for complex nonlinear systems like autonomous underwater vehicles (AUVs). In contrast, purely data-driven models, though convenient and quick to obtain, require a large number of observations and lack operational guarantees for safety-critical systems. Data-driven models leveraging available partially characterized dynamics have potential to provide reliable systems models in a typical data-limited scenario for high value complex systems, thereby avoiding months of expensive expert modeling time. In this work we explore this middle-ground between expert-modeled and pure data-driven modeling. We present control-oriented parametric models with varying levels of domain-awareness that exploit known system structure and prior physics knowledge to create constrained deep neural dynamical system models. We employ universal differential equations to construct data-driven blackbox and graybox representations of the AUV dynamics. In addition, we explore a hybrid formulation that explicitly models the residual error related to imperfect graybox models. We compare the prediction performance of the learned models for different distributions of initial conditions and control inputs to assess their accuracy, generalization, and suitability for control.

Differentiable Predictive Control with Safety Guarantees: A Control Barrier Function Approach

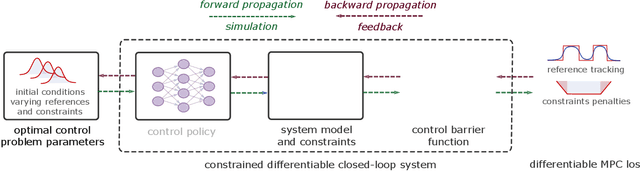
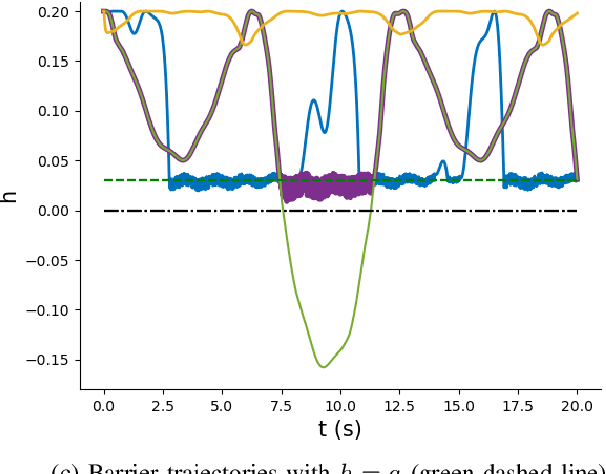
We develop a novel form of differentiable predictive control (DPC) with safety and robustness guarantees based on control barrier functions. DPC is an unsupervised learning-based method for obtaining approximate solutions to explicit model predictive control (MPC) problems. In DPC, the predictive control policy parametrized by a neural network is optimized offline via direct policy gradients obtained by automatic differentiation of the MPC problem. The proposed approach exploits a new form of sampled-data barrier function to enforce offline and online safety requirements in DPC settings while only interrupting the neural network-based controller near the boundary of the safe set. The effectiveness of the proposed approach is demonstrated in simulation.

Structural Inference of Networked Dynamical Systems with Universal Differential Equations

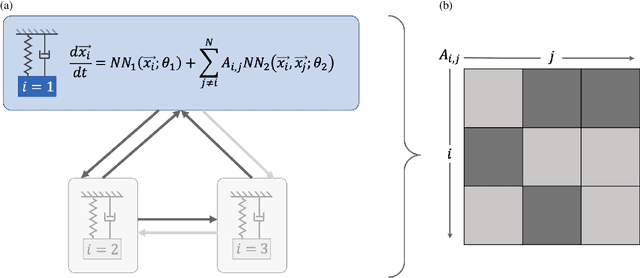
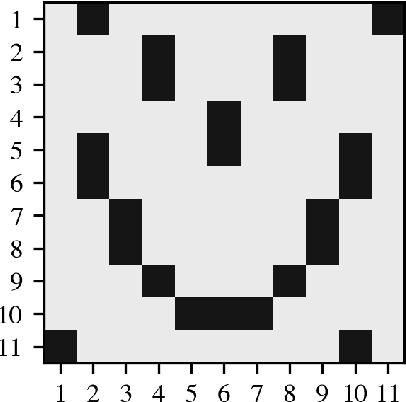
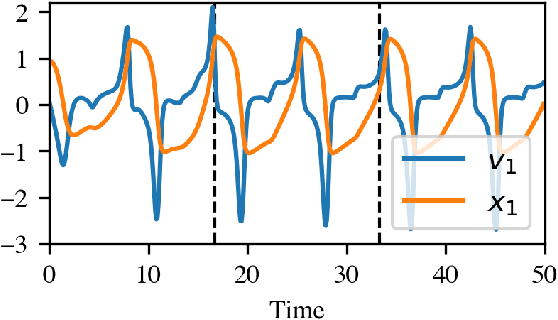
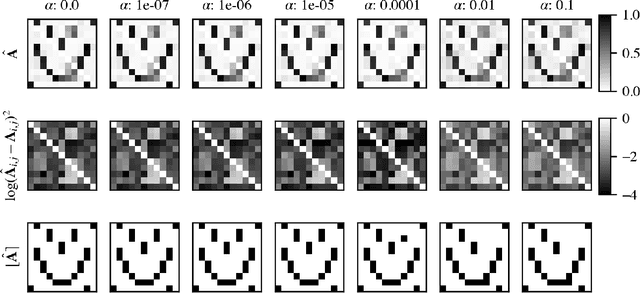
Networked dynamical systems are common throughout science in engineering; e.g., biological networks, reaction networks, power systems, and the like. For many such systems, nonlinearity drives populations of identical (or near-identical) units to exhibit a wide range of nontrivial behaviors, such as the emergence of coherent structures (e.g., waves and patterns) or otherwise notable dynamics (e.g., synchrony and chaos). In this work, we seek to infer (i) the intrinsic physics of a base unit of a population, (ii) the underlying graphical structure shared between units, and (iii) the coupling physics of a given networked dynamical system given observations of nodal states. These tasks are formulated around the notion of the Universal Differential Equation, whereby unknown dynamical systems can be approximated with neural networks, mathematical terms known a priori (albeit with unknown parameterizations), or combinations of the two. We demonstrate the value of these inference tasks by investigating not only future state predictions but also the inference of system behavior on varied network topologies. The effectiveness and utility of these methods is shown with their application to canonical networked nonlinear coupled oscillators.

Neural Lyapunov Differentiable Predictive Control

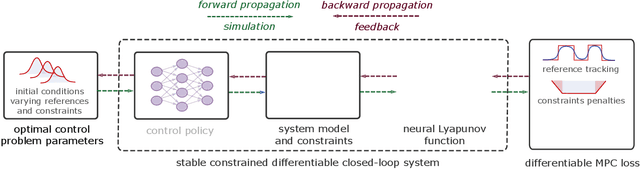
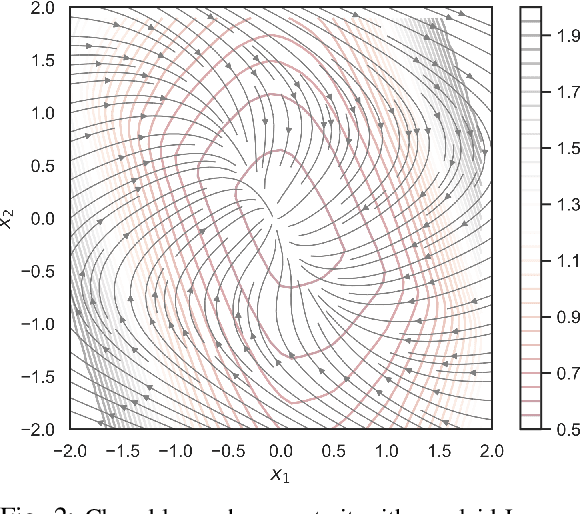
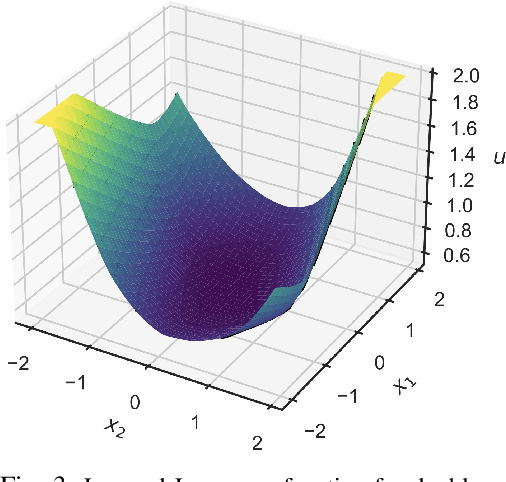
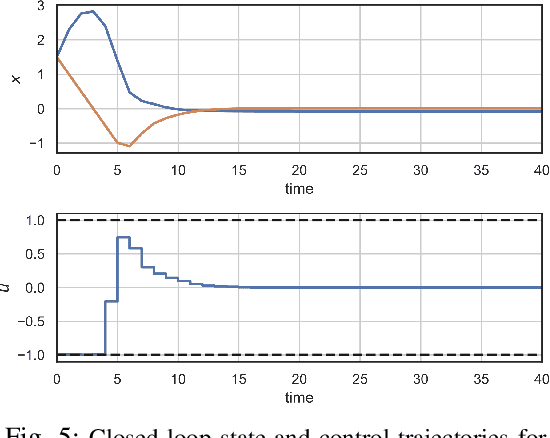
We present a learning-based predictive control methodology using the differentiable programming framework with probabilistic Lyapunov-based stability guarantees. The neural Lyapunov differentiable predictive control (NLDPC) learns the policy by constructing a computational graph encompassing the system dynamics, state and input constraints, and the necessary Lyapunov certification constraints, and thereafter using the automatic differentiation to update the neural policy parameters. In conjunction, our approach jointly learns a Lyapunov function that certifies the regions of state-space with stable dynamics. We also provide a sampling-based statistical guarantee for the training of NLDPC from the distribution of initial conditions. Our offline training approach provides a computationally efficient and scalable alternative to classical explicit model predictive control solutions. We substantiate the advantages of the proposed approach with simulations to stabilize the double integrator model and on an example of controlling an aircraft model.

Learning Stochastic Parametric Differentiable Predictive Control Policies

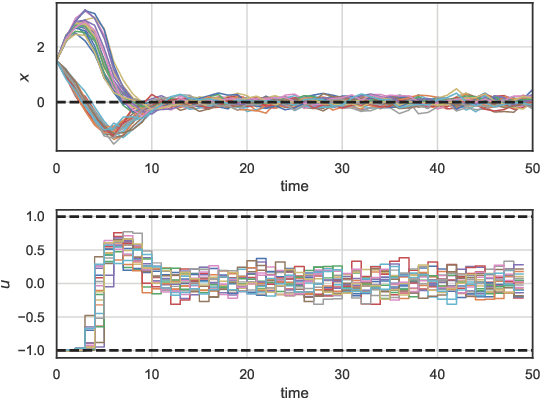
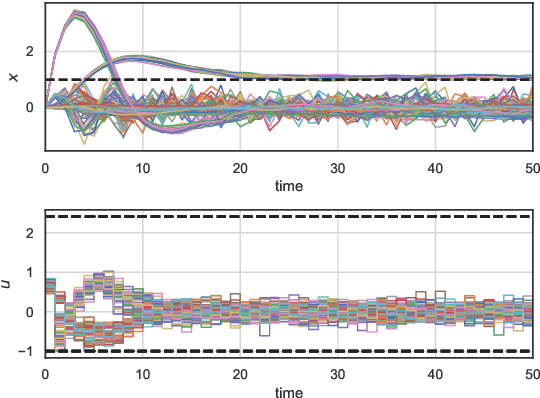
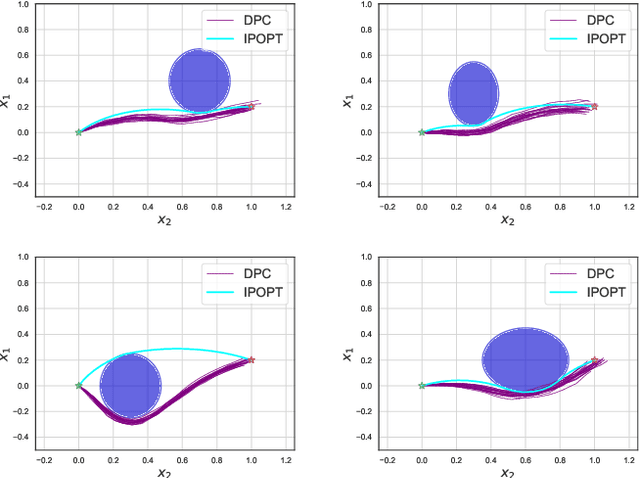
The problem of synthesizing stochastic explicit model predictive control policies is known to be quickly intractable even for systems of modest complexity when using classical control-theoretic methods. To address this challenge, we present a scalable alternative called stochastic parametric differentiable predictive control (SP-DPC) for unsupervised learning of neural control policies governing stochastic linear systems subject to nonlinear chance constraints. SP-DPC is formulated as a deterministic approximation to the stochastic parametric constrained optimal control problem. This formulation allows us to directly compute the policy gradients via automatic differentiation of the problem's value function, evaluated over sampled parameters and uncertainties. In particular, the computed expectation of the SP-DPC problem's value function is backpropagated through the closed-loop system rollouts parametrized by a known nominal system dynamics model and neural control policy which allows for direct model-based policy optimization. We provide theoretical probabilistic guarantees for policies learned via the SP-DPC method on closed-loop stability and chance constraints satisfaction. Furthermore, we demonstrate the computational efficiency and scalability of the proposed policy optimization algorithm in three numerical examples, including systems with a large number of states or subject to nonlinear constraints.

Deep Learning Explicit Differentiable Predictive Control Laws for Buildings

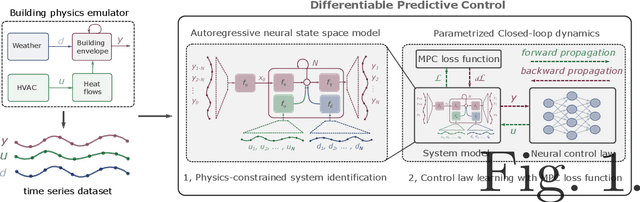
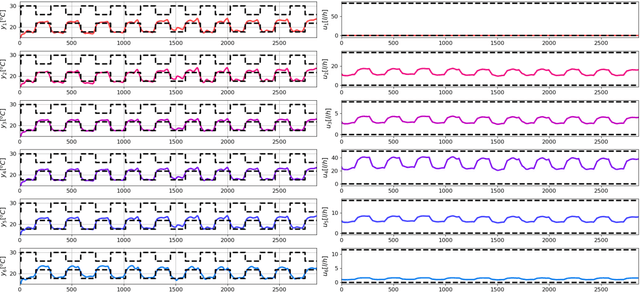
We present a differentiable predictive control (DPC) methodology for learning constrained control laws for unknown nonlinear systems. DPC poses an approximate solution to multiparametric programming problems emerging from explicit nonlinear model predictive control (MPC). Contrary to approximate MPC, DPC does not require supervision by an expert controller. Instead, a system dynamics model is learned from the observed system's dynamics, and the neural control law is optimized offline by leveraging the differentiable closed-loop system model. The combination of a differentiable closed-loop system and penalty methods for constraint handling of system outputs and inputs allows us to optimize the control law's parameters directly by backpropagating economic MPC loss through the learned system model. The control performance of the proposed DPC method is demonstrated in simulation using learned model of multi-zone building thermal dynamics.

Randomized Algorithms for Scientific Computing (RASC)

Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.

Constrained Block Nonlinear Neural Dynamical Models

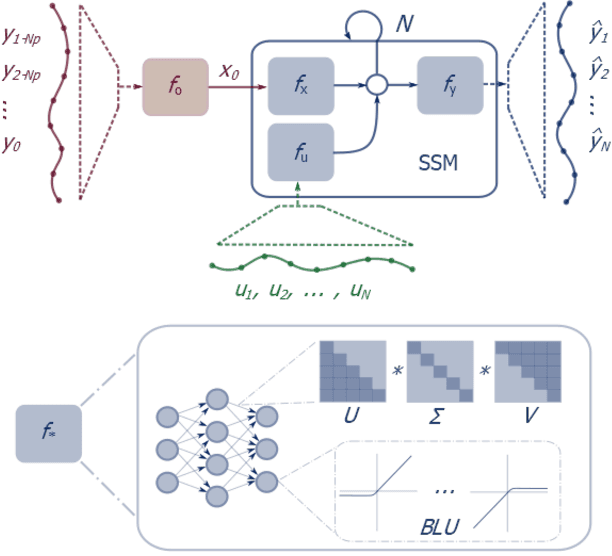
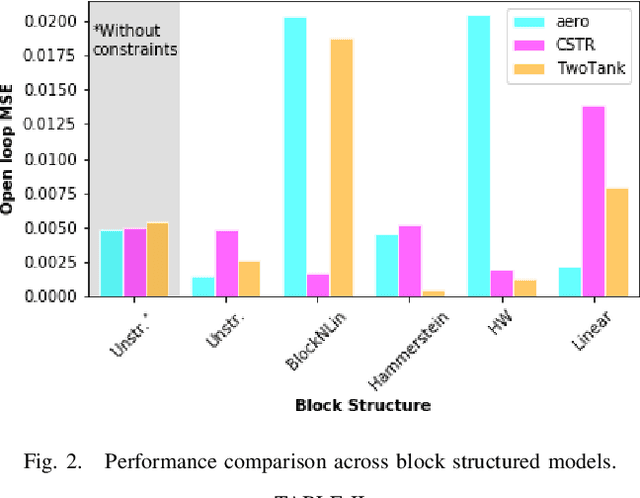
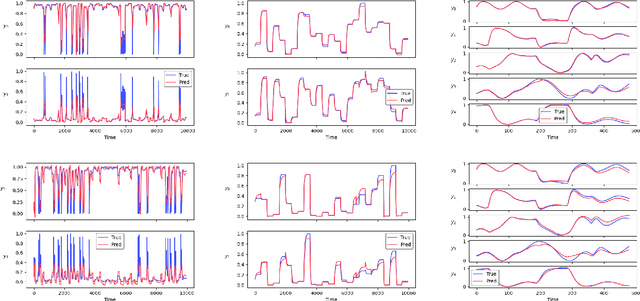
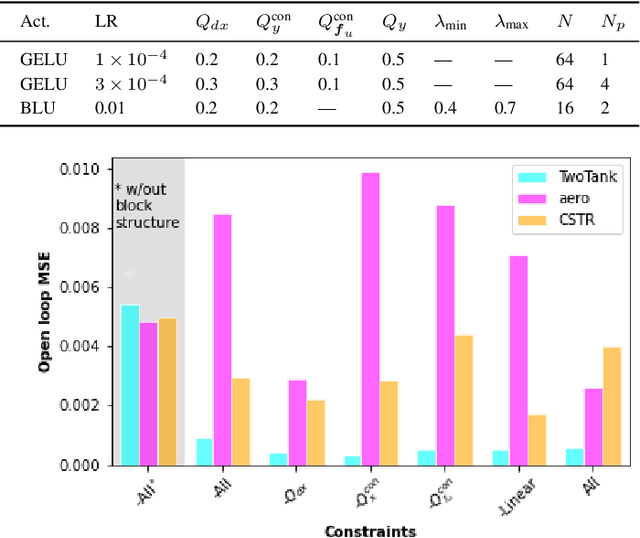
Neural network modules conditioned by known priors can be effectively trained and combined to represent systems with nonlinear dynamics. This work explores a novel formulation for data-efficient learning of deep control-oriented nonlinear dynamical models by embedding local model structure and constraints. The proposed method consists of neural network blocks that represent input, state, and output dynamics with constraints placed on the network weights and system variables. For handling partially observable dynamical systems, we utilize a state observer neural network to estimate the states of the system's latent dynamics. We evaluate the performance of the proposed architecture and training methods on system identification tasks for three nonlinear systems: a continuous stirred tank reactor, a two tank interacting system, and an aerodynamics body. Models optimized with a few thousand system state observations accurately represent system dynamics in open loop simulation over thousands of time steps from a single set of initial conditions. Experimental results demonstrate an order of magnitude reduction in open-loop simulation mean squared error for our constrained, block-structured neural models when compared to traditional unstructured and unconstrained neural network models.

Spectral Analysis and Stability of Deep Neural Dynamics

Our modern history of deep learning follows the arc of famous emergent disciplines in engineering (e.g. aero- and fluid dynamics) when theory lagged behind successful practical applications. Viewing neural networks from a dynamical systems perspective, in this work, we propose a novel characterization of deep neural networks as pointwise affine maps, making them accessible to a broader range of analysis methods to help close the gap between theory and practice. We begin by showing the equivalence of neural networks with parameter-varying affine maps parameterized by the state (feature) vector. As the paper's main results, we provide necessary and sufficient conditions for the global stability of generic deep feedforward neural networks. Further, we identify links between the spectral properties of layer-wise weight parametrizations, different activation functions, and their effect on the overall network's eigenvalue spectra. We analyze a range of neural networks with varying weight initializations, activation functions, bias terms, and depths. Our view of neural networks as affine parameter varying maps allows us to "crack open the black box" of global neural network dynamical behavior through visualization of stationary points, regions of attraction, state-space partitioning, eigenvalue spectra, and stability properties. Our analysis covers neural networks both as an end-to-end function and component-wise without simplifying assumptions or approximations. The methods we develop here provide tools to establish relationships between global neural dynamical properties and their constituent components which can aid in the principled design of neural networks for dynamics modeling and optimal control.