Tensor Decomposition Meets RKHS: Efficient Algorithms for Smooth and Misaligned Data

The canonical polyadic (CP) tensor decomposition decomposes a multidimensional data array into a sum of outer products of finite-dimensional vectors. Instead, we can replace some or all of the vectors with continuous functions (infinite-dimensional vectors) from a reproducing kernel Hilbert space (RKHS). We refer to tensors with some infinite-dimensional modes as quasitensors, and the approach of decomposing a tensor with some continuous RKHS modes is referred to as CP-HiFi (hybrid infinite and finite dimensional) tensor decomposition. An advantage of CP-HiFi is that it can enforce smoothness in the infinite dimensional modes. Further, CP-HiFi does not require the observed data to lie on a regular and finite rectangular grid and naturally incorporates misaligned data. We detail the methodology and illustrate it on a synthetic example.

Convergence of Alternating Gradient Descent for Matrix Factorization

We consider alternating gradient descent (AGD) with fixed step size $\eta > 0$, applied to the asymmetric matrix factorization objective. We show that, for a rank-$r$ matrix $\mathbf{A} \in \mathbb{R}^{m \times n}$, $T = \left( \left(\frac{\sigma_1(\mathbf{A})}{\sigma_r(\mathbf{A})}\right)^2 \log(1/\epsilon)\right)$ iterations of alternating gradient descent suffice to reach an $\epsilon$-optimal factorization $\| \mathbf{A} - \mathbf{X}_T^{\vphantom{\intercal}} \mathbf{Y}_T^{\intercal} \|_{\rm F}^2 \leq \epsilon \| \mathbf{A} \|_{\rm F}^2$ with high probability starting from an atypical random initialization. The factors have rank $d>r$ so that $\mathbf{X}_T\in\mathbb{R}^{m \times d}$ and $\mathbf{Y}_T \in\mathbb{R}^{n \times d}$. Experiments suggest that our proposed initialization is not merely of theoretical benefit, but rather significantly improves convergence of gradient descent in practice. Our proof is conceptually simple: a uniform PL-inequality and uniform Lipschitz smoothness constant are guaranteed for a sufficient number of iterations, starting from our random initialization. Our proof method should be useful for extending and simplifying convergence analyses for a broader class of nonconvex low-rank factorization problems.

Tensor Moments of Gaussian Mixture Models: Theory and Applications

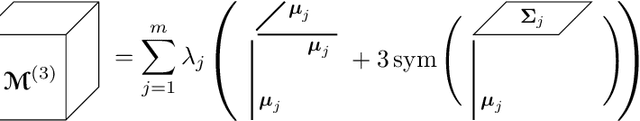
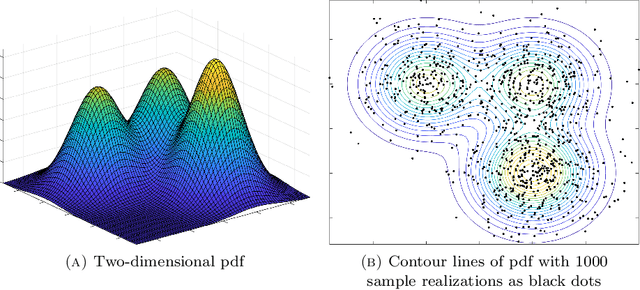
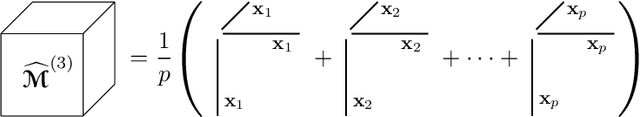
Gaussian mixture models (GMM) are fundamental tools in statistical and data sciences. We study the moments of multivariate Gaussians and GMMs. The $d$-th moment of an $n$-dimensional random variable is a symmetric $d$-way tensor of size $n^d$, so working with moments naively is assumed to be prohibitively expensive for $d>2$ and larger values of $n$. In this work, we develop theory and numerical methods for implicit computations with moment tensors of GMMs, reducing the computational and storage costs to $\mathcal{O}(n^2)$ and $\mathcal{O}(n^3)$, respectively, for general covariance matrices, and to $\mathcal{O}(n)$ and $\mathcal{O}(n)$, respectively, for diagonal ones. We derive concise analytic expressions for the moments in terms of symmetrized tensor products, relying on the correspondence between symmetric tensors and homogeneous polynomials, and combinatorial identities involving Bell polynomials. The primary application of this theory is to estimating GMM parameters from a set of observations, when formulated as a moment-matching optimization problem. If there is a known and common covariance matrix, we also show it is possible to debias the data observations, in which case the problem of estimating the unknown means reduces to symmetric CP tensor decomposition. Numerical results validate and illustrate the numerical efficiency of our approaches. This work potentially opens the door to the competitiveness of the method of moments as compared to expectation maximization methods for parameter estimation of GMMs.

Streaming Generalized Canonical Polyadic Tensor Decompositions

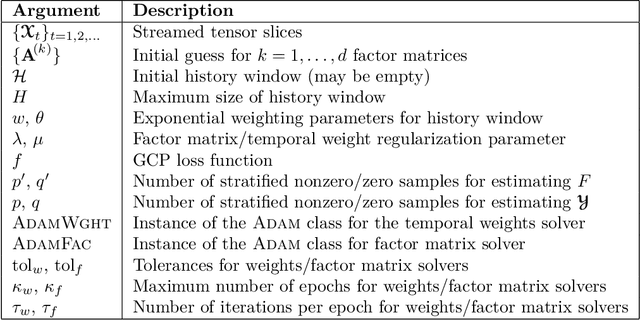
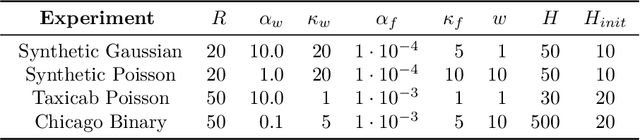
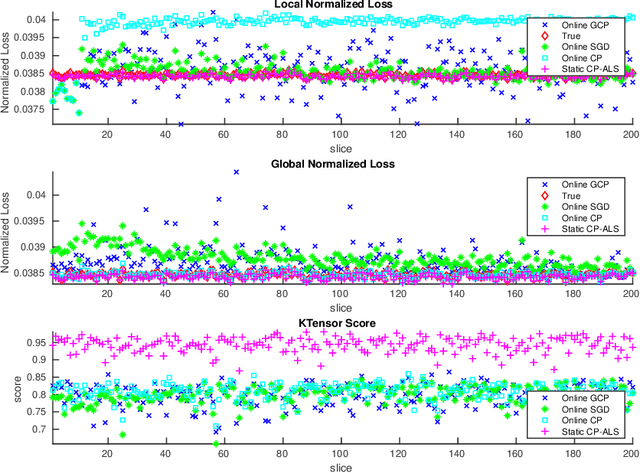
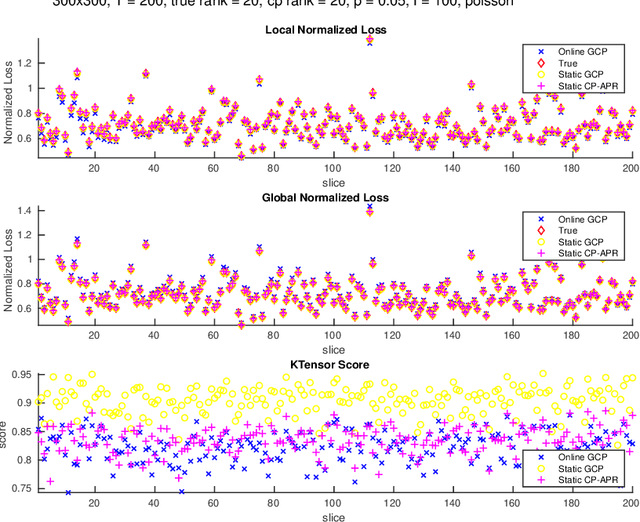
In this paper, we develop a method which we call OnlineGCP for computing the Generalized Canonical Polyadic (GCP) tensor decomposition of streaming data. GCP differs from traditional canonical polyadic (CP) tensor decompositions as it allows for arbitrary objective functions which the CP model attempts to minimize. This approach can provide better fits and more interpretable models when the observed tensor data is strongly non-Gaussian. In the streaming case, tensor data is gradually observed over time and the algorithm must incrementally update a GCP factorization with limited access to prior data. In this work, we extend the GCP formalism to the streaming context by deriving a GCP optimization problem to be solved as new tensor data is observed, formulate a tunable history term to balance reconstruction of recently observed data with data observed in the past, develop a scalable solution strategy based on segregated solves using stochastic gradient descent methods, describe a software implementation that provides performance and portability to contemporary CPU and GPU architectures and integrates with Matlab for enhanced useability, and demonstrate the utility and performance of the approach and software on several synthetic and real tensor data sets.

Randomized Algorithms for Scientific Computing (RASC)

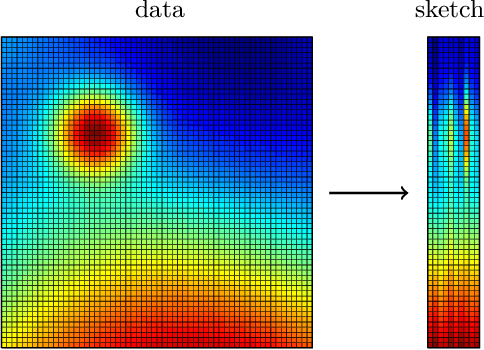
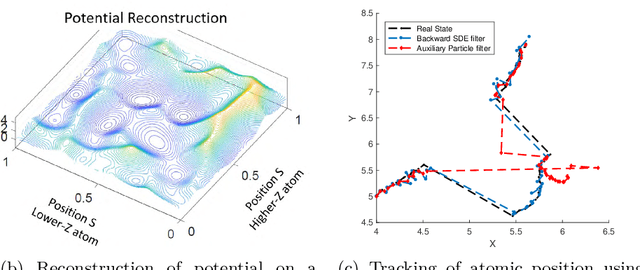
Randomized algorithms have propelled advances in artificial intelligence and represent a foundational research area in advancing AI for Science. Future advancements in DOE Office of Science priority areas such as climate science, astrophysics, fusion, advanced materials, combustion, and quantum computing all require randomized algorithms for surmounting challenges of complexity, robustness, and scalability. This report summarizes the outcomes of that workshop, "Randomized Algorithms for Scientific Computing (RASC)," held virtually across four days in December 2020 and January 2021.

Stochastic Gradients for Large-Scale Tensor Decomposition

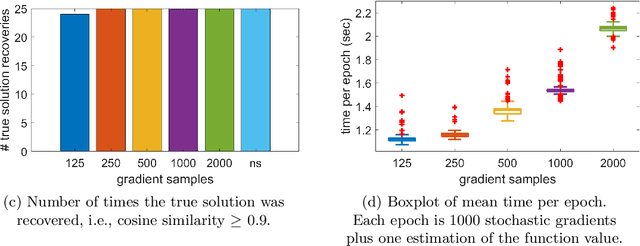
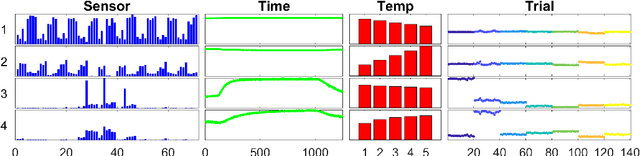
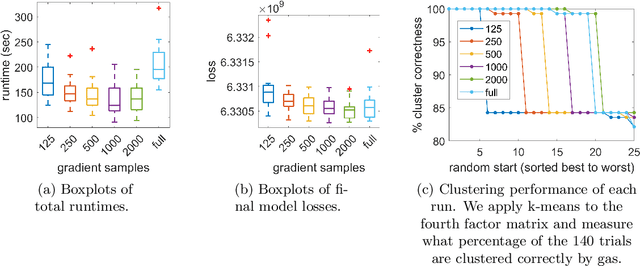
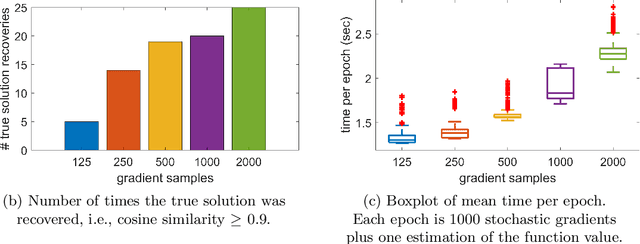
Tensor decomposition is a well-known tool for multiway data analysis. This work proposes using stochastic gradients for efficient generalized canonical polyadic (GCP) tensor decomposition of large-scale tensors. GCP tensor decomposition is a recently proposed version of tensor decomposition that allows for a variety of loss functions such as logistic loss for binary data or Huber loss for robust estimation. The stochastic gradient is formed from randomly sampled elements of the tensor. For dense tensors, we simply use uniform sampling. For sparse tensors, we propose two types of stratified sampling that give precedence to sampling nonzeros. Numerical results demonstrate the advantages of the proposed approach and its scalability to large-scale problems.

XPCA: Extending PCA for a Combination of Discrete and Continuous Variables

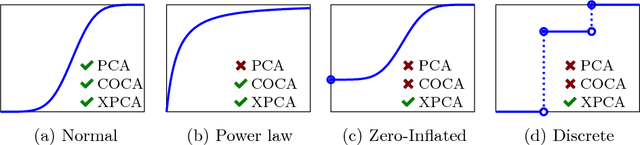
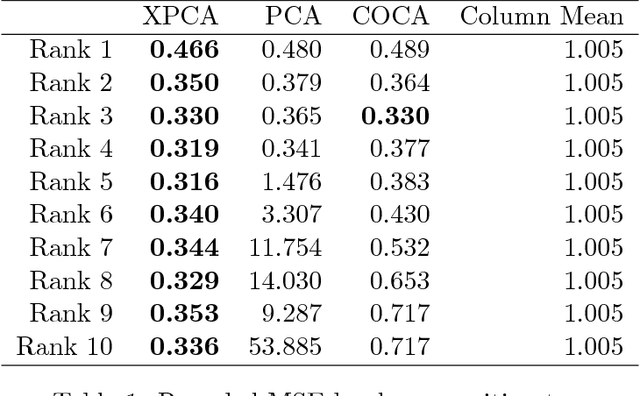
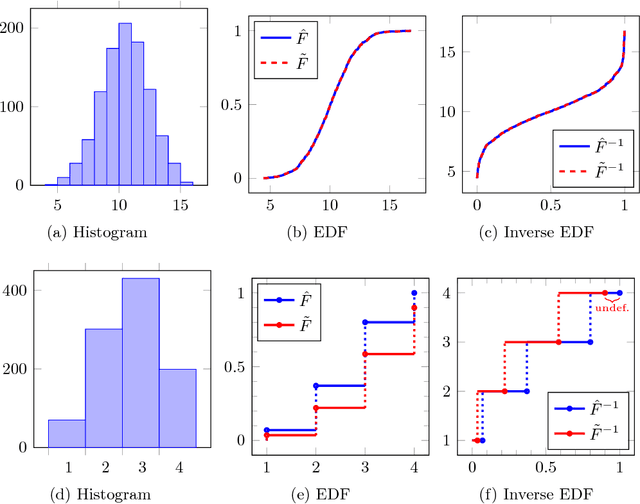
Principal component analysis (PCA) is arguably the most popular tool in multivariate exploratory data analysis. In this paper, we consider the question of how to handle heterogeneous variables that include continuous, binary, and ordinal. In the probabilistic interpretation of low-rank PCA, the data has a normal multivariate distribution and, therefore, normal marginal distributions for each column. If some marginals are continuous but not normal, the semiparametric copula-based principal component analysis (COCA) method is an alternative to PCA that combines a Gaussian copula with nonparametric marginals. If some marginals are discrete or semi-continuous, we propose a new extended PCA (XPCA) method that also uses a Gaussian copula and nonparametric marginals and accounts for discrete variables in the likelihood calculation by integrating over appropriate intervals. Like PCA, the factors produced by XPCA can be used to find latent structure in data, build predictive models, and perform dimensionality reduction. We present the new model, its induced likelihood function, and a fitting algorithm which can be applied in the presence of missing data. We demonstrate how to use XPCA to produce an estimated full conditional distribution for each data point, and use this to produce to provide estimates for missing data that are automatically range respecting. We compare the methods as applied to simulated and real-world data sets that have a mixture of discrete and continuous variables.

Generalized Canonical Polyadic Tensor Decomposition

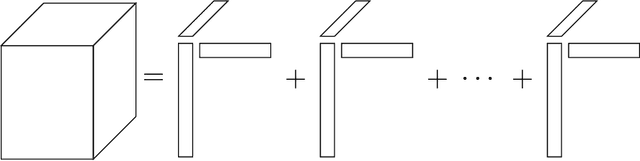
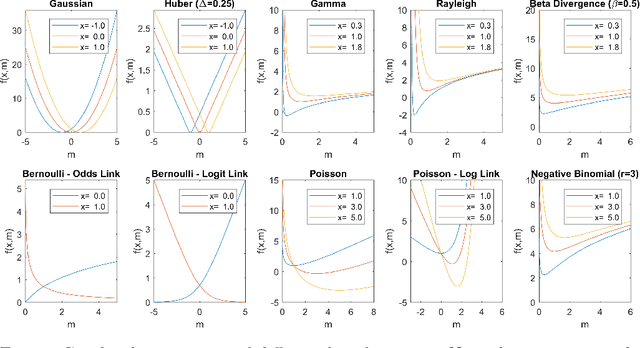
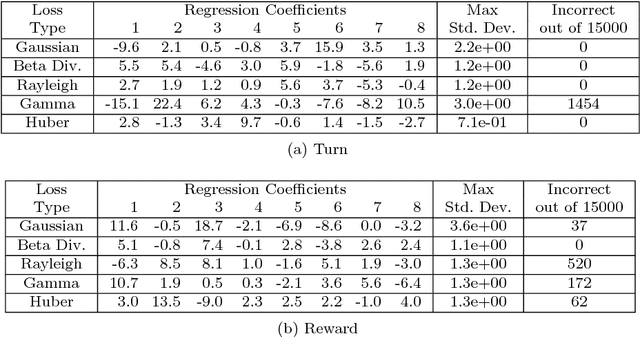
Tensor decomposition is a fundamental unsupervised machine learning method in data science, with applications including network analysis and sensor data processing. This work develops a generalized canonical polyadic (GCP) low-rank tensor decomposition that allows other loss functions besides squared error. For instance, we can use logistic loss or Kullback-Leibler divergence, enabling tensor decomposition for binary or count data. We present a variety statistically-motivated loss functions for various scenarios. We provide a generalized framework for computing gradients and handling missing data that enables the use of standard optimization methods for fitting the model. We demonstrate the flexibility of GCP on several real-world examples including interactions in a social network, neural activity in a mouse, and monthly rainfall measurements in India.

COMET: A Recipe for Learning and Using Large Ensembles on Massive Data

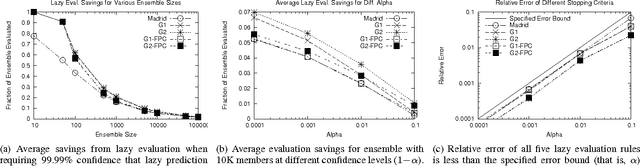
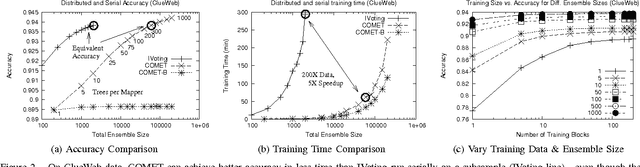
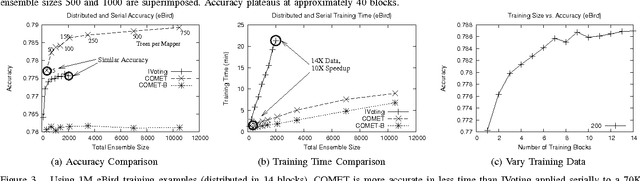
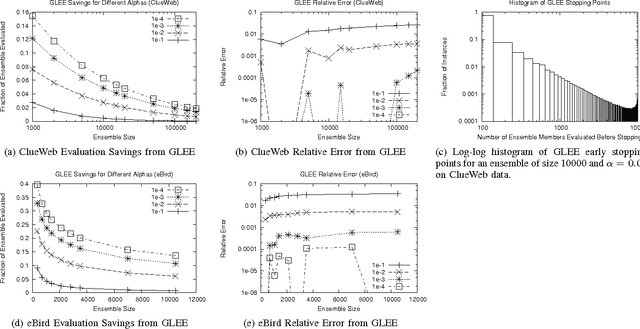
COMET is a single-pass MapReduce algorithm for learning on large-scale data. It builds multiple random forest ensembles on distributed blocks of data and merges them into a mega-ensemble. This approach is appropriate when learning from massive-scale data that is too large to fit on a single machine. To get the best accuracy, IVoting should be used instead of bagging to generate the training subset for each decision tree in the random forest. Experiments with two large datasets (5GB and 50GB compressed) show that COMET compares favorably (in both accuracy and training time) to learning on a subsample of data using a serial algorithm. Finally, we propose a new Gaussian approach for lazy ensemble evaluation which dynamically decides how many ensemble members to evaluate per data point; this can reduce evaluation cost by 100X or more.

All-at-once Optimization for Coupled Matrix and Tensor Factorizations

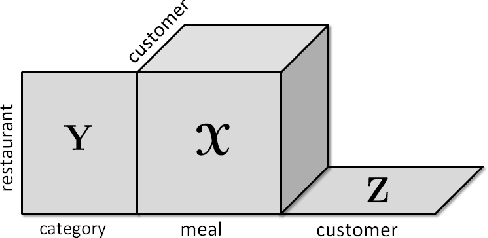
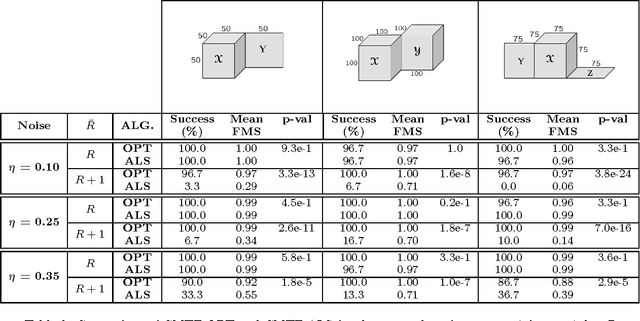
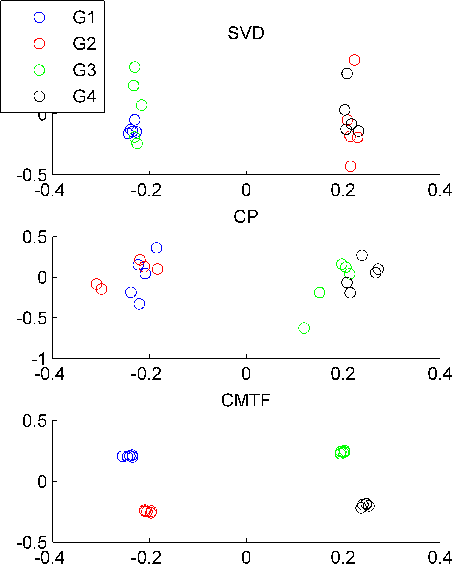
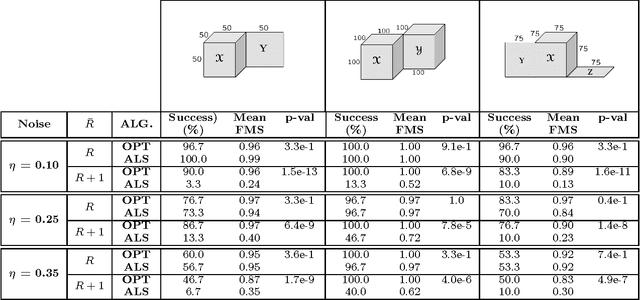
Joint analysis of data from multiple sources has the potential to improve our understanding of the underlying structures in complex data sets. For instance, in restaurant recommendation systems, recommendations can be based on rating histories of customers. In addition to rating histories, customers' social networks (e.g., Facebook friendships) and restaurant categories information (e.g., Thai or Italian) can also be used to make better recommendations. The task of fusing data, however, is challenging since data sets can be incomplete and heterogeneous, i.e., data consist of both matrices, e.g., the person by person social network matrix or the restaurant by category matrix, and higher-order tensors, e.g., the "ratings" tensor of the form restaurant by meal by person. In this paper, we are particularly interested in fusing data sets with the goal of capturing their underlying latent structures. We formulate this problem as a coupled matrix and tensor factorization (CMTF) problem where heterogeneous data sets are modeled by fitting outer-product models to higher-order tensors and matrices in a coupled manner. Unlike traditional approaches solving this problem using alternating algorithms, we propose an all-at-once optimization approach called CMTF-OPT (CMTF-OPTimization), which is a gradient-based optimization approach for joint analysis of matrices and higher-order tensors. We also extend the algorithm to handle coupled incomplete data sets. Using numerical experiments, we demonstrate that the proposed all-at-once approach is more accurate than the alternating least squares approach.