A Little Human Data Goes A Long Way

Faced with an expensive human annotation process, creators of NLP systems increasingly turn to synthetic data generation. While this method shows promise, the extent to which synthetic data can replace human annotation is poorly understood. We investigate the use of synthetic data in Fact Verification (FV) and Question Answering (QA) by studying the effects of incrementally replacing human generated data with synthetic points on eight diverse datasets. Strikingly, replacing up to 90% of the training data only marginally decreases performance, but replacing the final 10% leads to severe declines. We find that models trained on purely synthetic data can be reliably improved by including as few as 125 human generated data points. We show that matching the performance gain of just a little additional human data (only 200 points) requires an order of magnitude more synthetic data and estimate price ratios at which human annotation would be a more cost-effective solution. Our results suggest that even when human annotation at scale is infeasible, there is great value to having a small proportion of the dataset being human generated.

Controllable Text Generation in the Instruction-Tuning Era

While most research on controllable text generation has focused on steering base Language Models, the emerging instruction-tuning and prompting paradigm offers an alternate approach to controllability. We compile and release ConGenBench, a testbed of 17 different controllable generation tasks, using a subset of it to benchmark the performance of 9 different baselines and methods on Instruction-tuned Language Models. To our surprise, we find that prompting-based approaches outperform controllable text generation methods on most datasets and tasks, highlighting a need for research on controllable text generation with Instruction-tuned Language Models in specific. Prompt-based approaches match human performance on most stylistic tasks while lagging on structural tasks, foregrounding a need to study more varied constraints and more challenging stylistic tasks. To facilitate such research, we provide an algorithm that uses only a task dataset and a Large Language Model with in-context capabilities to automatically generate a constraint dataset. This method eliminates the fields dependence on pre-curated constraint datasets, hence vastly expanding the range of constraints that can be studied in the future.

FeedbackLogs: Recording and Incorporating Stakeholder Feedback into Machine Learning Pipelines

Even though machine learning (ML) pipelines affect an increasing array of stakeholders, there is little work on how input from stakeholders is recorded and incorporated. We propose FeedbackLogs, addenda to existing documentation of ML pipelines, to track the input of multiple stakeholders. Each log records important details about the feedback collection process, the feedback itself, and how the feedback is used to update the ML pipeline. In this paper, we introduce and formalise a process for collecting a FeedbackLog. We also provide concrete use cases where FeedbackLogs can be employed as evidence for algorithmic auditing and as a tool to record updates based on stakeholder feedback.

PromptNER: Prompting For Named Entity Recognition

In a surprising turn, Large Language Models (LLMs) together with a growing arsenal of prompt-based heuristics now offer powerful off-the-shelf approaches providing few-shot solutions to myriad classic NLP problems. However, despite promising early results, these LLM-based few-shot methods remain far from the state of the art in Named Entity Recognition (NER), where prevailing methods include learning representations via end-to-end structural understanding and fine-tuning on standard labeled corpora. In this paper, we introduce PromptNER, a new state-of-the-art algorithm for few-Shot and cross-domain NER. To adapt to any new NER task PromptNER requires a set of entity definitions in addition to the standard few-shot examples. Given a sentence, PromptNER prompts an LLM to produce a list of potential entities along with corresponding explanations justifying their compatibility with the provided entity type definitions. Remarkably, PromptNER achieves state-of-the-art performance on few-shot NER, achieving an 11% (absolute) improvement in F1 score on the ConLL dataset, and a 10% (absolute) improvement on the FewNERD dataset. PromptNER also moves the state of the art on Cross Domain NER, outperforming all prior methods (including those not limited to the few-shot setting), setting a new mark on all 5 CrossNER target domains, with an average F1 gain of 9%, despite using less than 2% of the available data.

The student becomes the master: Matching GPT3 on Scientific Factual Error Correction

Due to the prohibitively high cost of creating error correction datasets, most Factual Claim Correction methods rely on a powerful verification model to guide the correction process. This leads to a significant drop in performance in domains like Scientific Claim Correction, where good verification models do not always exist. In this work, we introduce a claim correction system that makes no domain assumptions and does not require a verifier but is able to outperform existing methods by an order of magnitude -- achieving 94% correction accuracy on the SciFact dataset, and 62.5% on the SciFact-Open dataset, compared to the next best methods 0.5% and 1.50% respectively. Our method leverages the power of prompting with LLMs during training to create a richly annotated dataset that can be used for fully supervised training and regularization. We additionally use a claim-aware decoding procedure to improve the quality of corrected claims. Our method is competitive with the very LLM that was used to generate the annotated dataset -- with GPT3.5 achieving 89.5% and 60% correction accuracy on SciFact and SciFact-Open, despite using 1250 times as many parameters as our model.

A Solver + Gradient Descent Training Algorithm for Deep Neural Networks

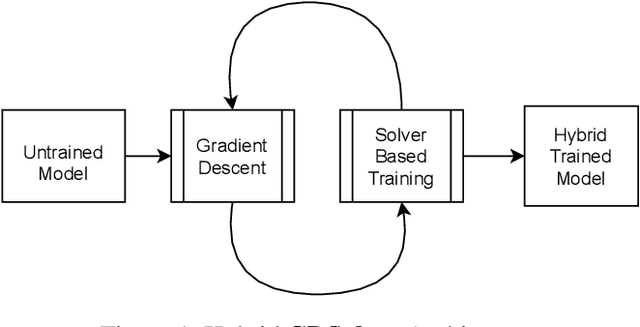
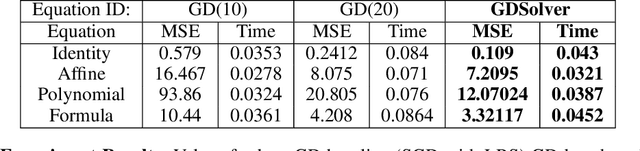
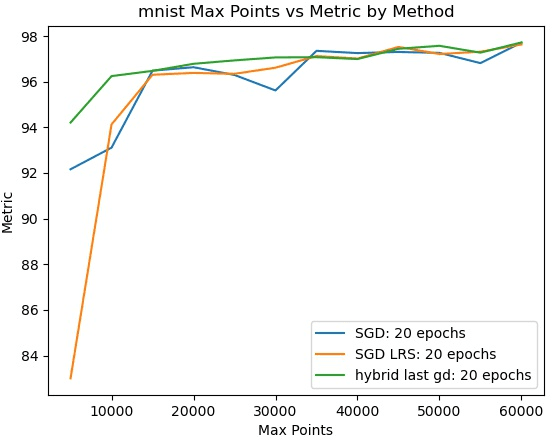
We present a novel hybrid algorithm for training Deep Neural Networks that combines the state-of-the-art Gradient Descent (GD) method with a Mixed Integer Linear Programming (MILP) solver, outperforming GD and variants in terms of accuracy, as well as resource and data efficiency for both regression and classification tasks. Our GD+Solver hybrid algorithm, called GDSolver, works as follows: given a DNN $D$ as input, GDSolver invokes GD to partially train $D$ until it gets stuck in a local minima, at which point GDSolver invokes an MILP solver to exhaustively search a region of the loss landscape around the weight assignments of $D$'s final layer parameters with the goal of tunnelling through and escaping the local minima. The process is repeated until desired accuracy is achieved. In our experiments, we find that GDSolver not only scales well to additional data and very large model sizes, but also outperforms all other competing methods in terms of rates of convergence and data efficiency. For regression tasks, GDSolver produced models that, on average, had 31.5% lower MSE in 48% less time, and for classification tasks on MNIST and CIFAR10, GDSolver was able to achieve the highest accuracy over all competing methods, using only 50% of the training data that GD baselines required.

Logic Guided Genetic Algorithms

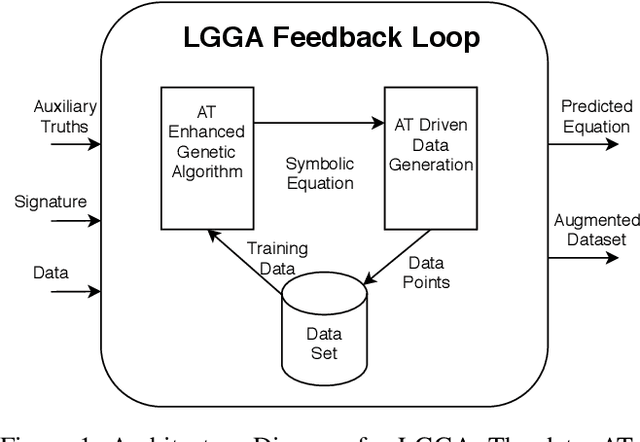
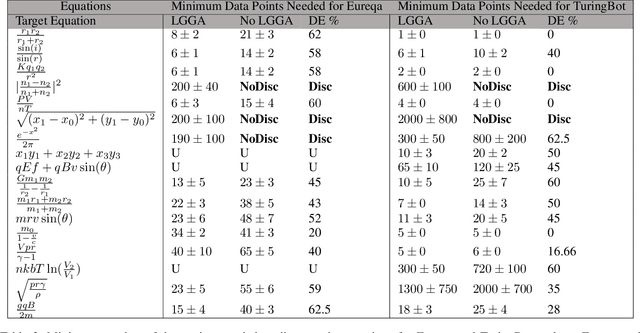
We present a novel Auxiliary Truth enhanced Genetic Algorithm (GA) that uses logical or mathematical constraints as a means of data augmentation as well as to compute loss (in conjunction with the traditional MSE), with the aim of increasing both data efficiency and accuracy of symbolic regression (SR) algorithms. Our method, logic-guided genetic algorithm (LGGA), takes as input a set of labelled data points and auxiliary truths (ATs) (mathematical facts known a priori about the unknown function the regressor aims to learn) and outputs a specially generated and curated dataset that can be used with any SR method. Three key insights underpin our method: first, SR users often know simple ATs about the function they are trying to learn. Second, whenever an SR system produces a candidate equation inconsistent with these ATs, we can compute a counterexample to prove the inconsistency, and further, this counterexample may be used to augment the dataset and fed back to the SR system in a corrective feedback loop. Third, the value addition of these ATs is that their use in both the loss function and the data augmentation process leads to better rates of convergence, accuracy, and data efficiency. We evaluate LGGA against state-of-the-art SR tools, namely, Eureqa and TuringBot on 16 physics equations from "The Feynman Lectures on Physics" book. We find that using these SR tools in conjunction with LGGA results in them solving up to 30.0% more equations, needing only a fraction of the amount of data compared to the same tool without LGGA, i.e., resulting in up to a 61.9% improvement in data efficiency.