Neural Simulated Annealing

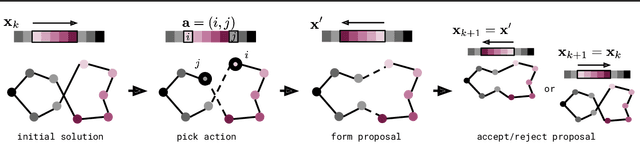
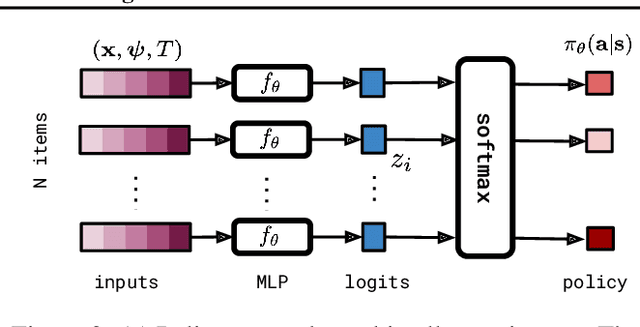
Simulated annealing (SA) is a stochastic global optimisation technique applicable to a wide range of discrete and continuous variable problems. Despite its simplicity, the development of an effective SA optimiser for a given problem hinges on a handful of carefully handpicked components; namely, neighbour proposal distribution and temperature annealing schedule. In this work, we view SA from a reinforcement learning perspective and frame the proposal distribution as a policy, which can be optimised for higher solution quality given a fixed computational budget. We demonstrate that this Neural SA with such a learnt proposal distribution, parametrised by small equivariant neural networks, outperforms SA baselines on a number of problems: Rosenbrock's function, the Knapsack problem, the Bin Packing problem, and the Travelling Salesperson problem. We also show that Neural SA scales well to large problems - generalising to significantly larger problems than the ones seen during training - while achieving comparable performance to popular off-the-shelf solvers and other machine learning methods in terms of solution quality and wall-clock time.

Lie Point Symmetry Data Augmentation for Neural PDE Solvers

Neural networks are increasingly being used to solve partial differential equations (PDEs), replacing slower numerical solvers. However, a critical issue is that neural PDE solvers require high-quality ground truth data, which usually must come from the very solvers they are designed to replace. Thus, we are presented with a proverbial chicken-and-egg problem. In this paper, we present a method, which can partially alleviate this problem, by improving neural PDE solver sample complexity -- Lie point symmetry data augmentation (LPSDA). In the context of PDEs, it turns out that we are able to quantitatively derive an exhaustive list of data transformations, based on the Lie point symmetry group of the PDEs in question, something not possible in other application areas. We present this framework and demonstrate how it can easily be deployed to improve neural PDE solver sample complexity by an order of magnitude.

MDP Homomorphic Networks: Group Symmetries in Reinforcement Learning

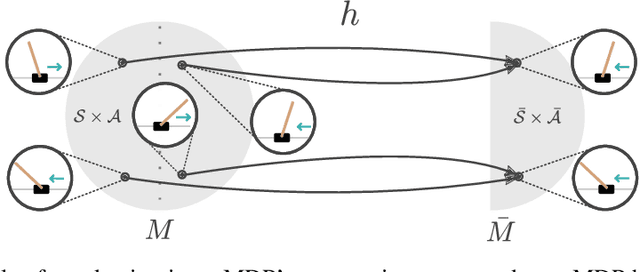
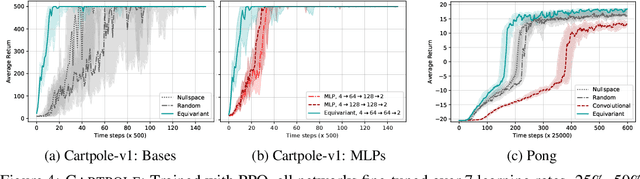
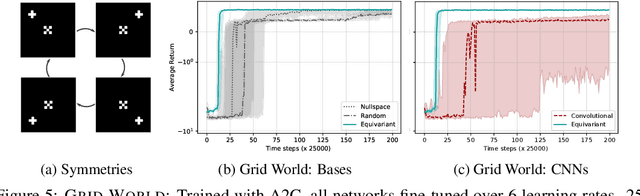
This paper introduces MDP homomorphic networks for deep reinforcement learning. MDP homomorphic networks are neural networks that are equivariant under symmetries in the joint state-action space of an MDP. Current approaches to deep reinforcement learning do not usually exploit knowledge about such structure. By building this prior knowledge into policy and value networks using an equivariance constraint, we can reduce the size of the solution space. We specifically focus on group-structured symmetries (invertible transformations). Additionally, we introduce an easy method for constructing equivariant network layers numerically, so the system designer need not solve the constraints by hand, as is typically done. We construct MDP homomorphic MLPs and CNNs that are equivariant under either a group of reflections or rotations. We show that such networks converge faster than unstructured baselines on CartPole, a grid world and Pong.

SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks

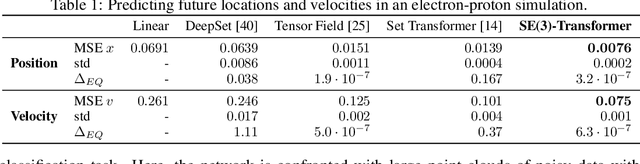
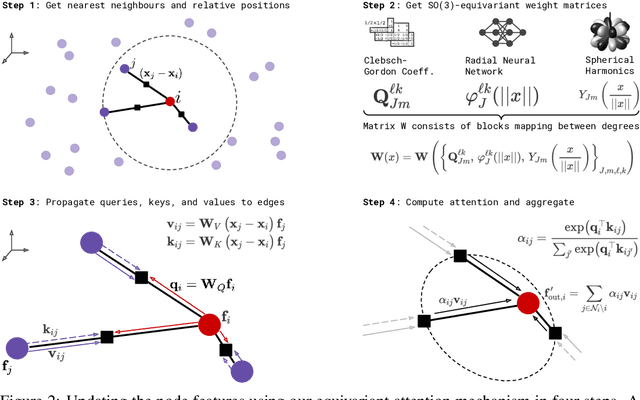
We introduce the SE(3)-Transformer, a variant of the self-attention module for 3D point clouds, which is equivariant under continuous 3D roto-translations. Equivariance is important to ensure stable and predictable performance in the presence of nuisance transformations of the data input. A positive corollary of equivariance is increased weight-tying within the model, leading to fewer trainable parameters and thus decreased sample complexity (i.e. we need less training data). The SE(3)-Transformer leverages the benefits of self-attention to operate on large point clouds with varying number of points, while guaranteeing SE(3)-equivariance for robustness. We evaluate our model on a toy $N$-body particle simulation dataset, showcasing the robustness of the predictions under rotations of the input. We further achieve competitive performance on two real-world datasets, ScanObjectNN and QM9. In all cases, our model outperforms a strong, non-equivariant attention baseline and an equivariant model without attention.

Deep Scale-spaces: Equivariance Over Scale

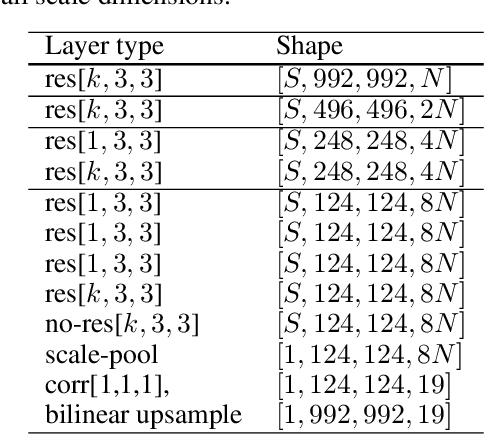
We introduce deep scale-spaces (DSS), a generalization of convolutional neural networks, exploiting the scale symmetry structure of conventional image recognition tasks. Put plainly, the class of an image is invariant to the scale at which it is viewed. We construct scale equivariant cross-correlations based on a principled extension of convolutions, grounded in the theory of scale-spaces and semigroups. As a very basic operation, these cross-correlations can be used in almost any modern deep learning architecture in a plug-and-play manner. We demonstrate our networks on the Patch Camelyon and Cityscapes datasets, to prove their utility and perform introspective studies to further understand their properties.

Reversible GANs for Memory-efficient Image-to-Image Translation

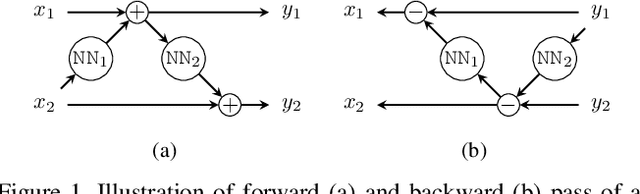
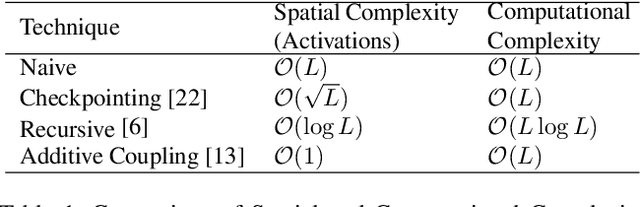
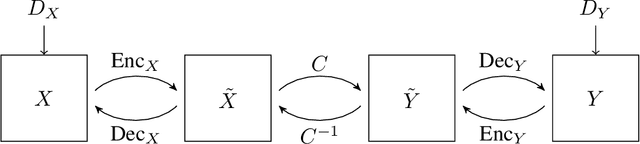
The Pix2pix and CycleGAN losses have vastly improved the qualitative and quantitative visual quality of results in image-to-image translation tasks. We extend this framework by exploring approximately invertible architectures which are well suited to these losses. These architectures are approximately invertible by design and thus partially satisfy cycle-consistency before training even begins. Furthermore, since invertible architectures have constant memory complexity in depth, these models can be built arbitrarily deep. We are able to demonstrate superior quantitative output on the Cityscapes and Maps datasets at near constant memory budget.

Virtual Adversarial Ladder Networks For Semi-supervised Learning

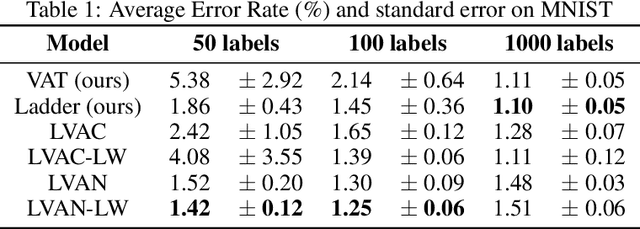
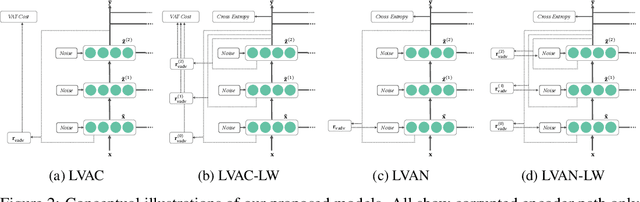
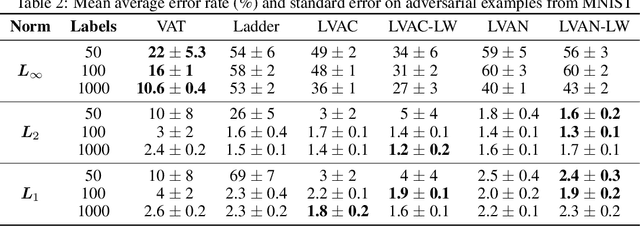
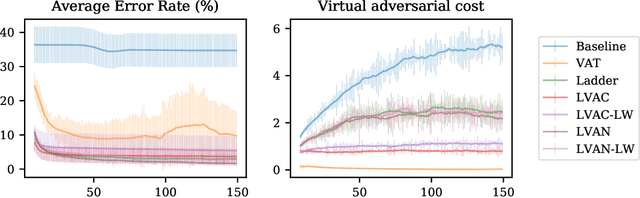
Semi-supervised learning (SSL) partially circumvents the high cost of labeling data by augmenting a small labeled dataset with a large and relatively cheap unlabeled dataset drawn from the same distribution. This paper offers a novel interpretation of two deep learning-based SSL approaches, ladder networks and virtual adversarial training (VAT), as applying distributional smoothing to their respective latent spaces. We propose a class of models that fuse these approaches. We achieve near-supervised accuracy with high consistency on the MNIST dataset using just 5 labels per class: our best model, ladder with layer-wise virtual adversarial noise (LVAN-LW), achieves 1.42% +/- 0.12 average error rate on the MNIST test set, in comparison with 1.62% +/- 0.65 reported for the ladder network. On adversarial examples generated with L2-normalized fast gradient method, LVAN-LW trained with 5 examples per class achieves average error rate 2.4% +/- 0.3 compared to 68.6% +/- 6.5 for the ladder network and 9.9% +/- 7.5 for VAT.

Interpretable Transformations with Encoder-Decoder Networks

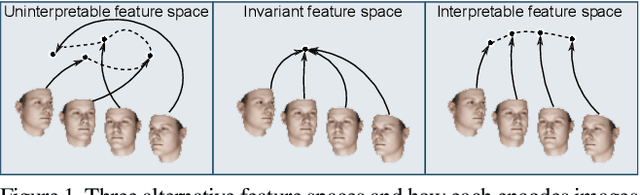
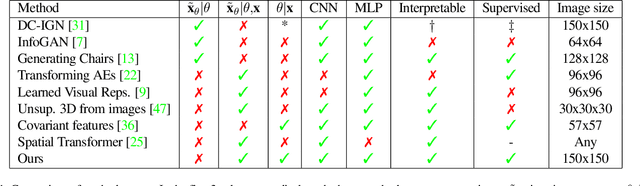
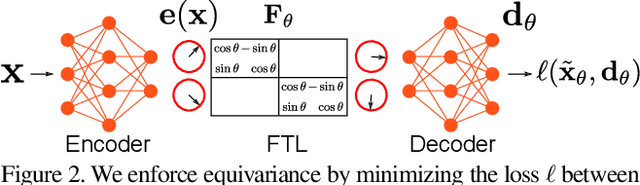
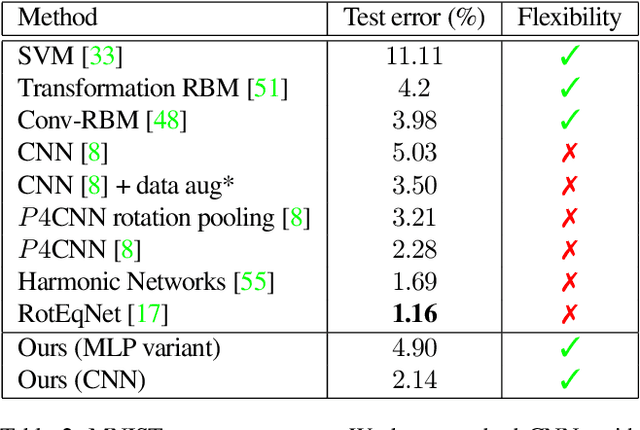
Deep feature spaces have the capacity to encode complex transformations of their input data. However, understanding the relative feature-space relationship between two transformed encoded images is difficult. For instance, what is the relative feature space relationship between two rotated images? What is decoded when we interpolate in feature space? Ideally, we want to disentangle confounding factors, such as pose, appearance, and illumination, from object identity. Disentangling these is difficult because they interact in very nonlinear ways. We propose a simple method to construct a deep feature space, with explicitly disentangled representations of several known transformations. A person or algorithm can then manipulate the disentangled representation, for example, to re-render an image with explicit control over parameterized degrees of freedom. The feature space is constructed using a transforming encoder-decoder network with a custom feature transform layer, acting on the hidden representations. We demonstrate the advantages of explicit disentangling on a variety of datasets and transformations, and as an aid for traditional tasks, such as classification.

Bayesian Image Quality Transfer with CNNs: Exploring Uncertainty in dMRI Super-Resolution

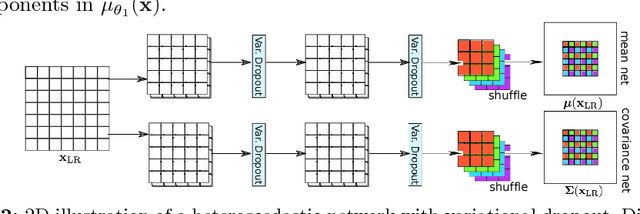
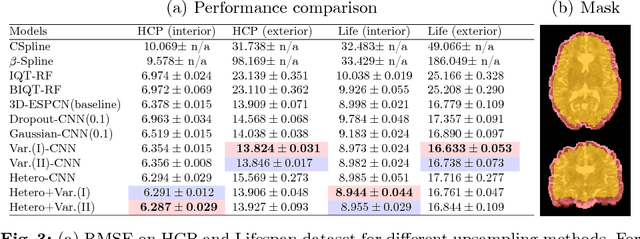
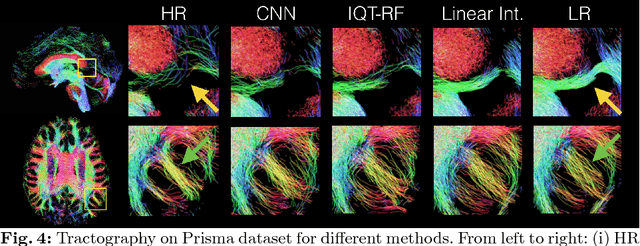
In this work, we investigate the value of uncertainty modeling in 3D super-resolution with convolutional neural networks (CNNs). Deep learning has shown success in a plethora of medical image transformation problems, such as super-resolution (SR) and image synthesis. However, the highly ill-posed nature of such problems results in inevitable ambiguity in the learning of networks. We propose to account for intrinsic uncertainty through a per-patch heteroscedastic noise model and for parameter uncertainty through approximate Bayesian inference in the form of variational dropout. We show that the combined benefits of both lead to the state-of-the-art performance SR of diffusion MR brain images in terms of errors compared to ground truth. We further show that the reduced error scores produce tangible benefits in downstream tractography. In addition, the probabilistic nature of the methods naturally confers a mechanism to quantify uncertainty over the super-resolved output. We demonstrate through experiments on both healthy and pathological brains the potential utility of such an uncertainty measure in the risk assessment of the super-resolved images for subsequent clinical use.

Harmonic Networks: Deep Translation and Rotation Equivariance

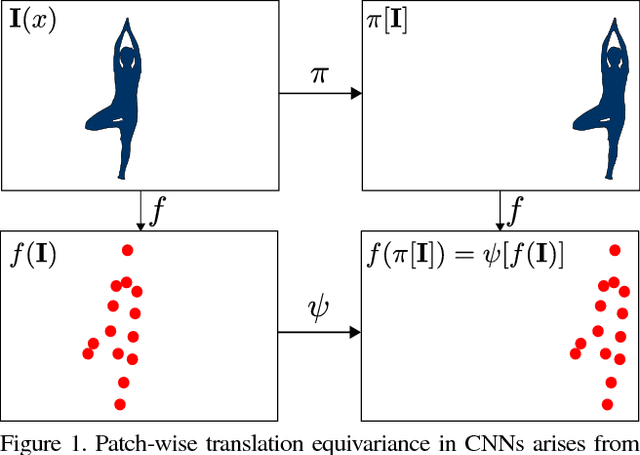
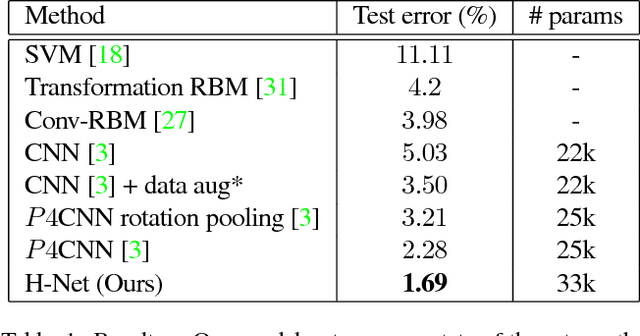
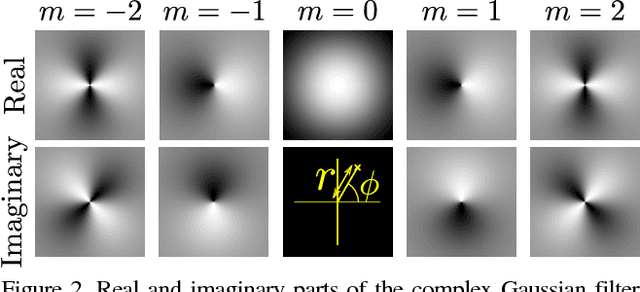
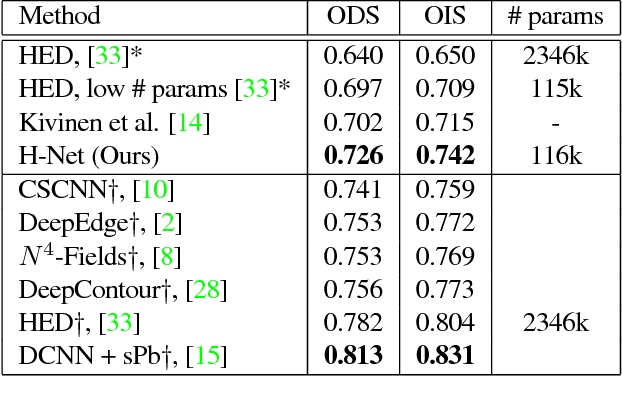
Translating or rotating an input image should not affect the results of many computer vision tasks. Convolutional neural networks (CNNs) are already translation equivariant: input image translations produce proportionate feature map translations. This is not the case for rotations. Global rotation equivariance is typically sought through data augmentation, but patch-wise equivariance is more difficult. We present Harmonic Networks or H-Nets, a CNN exhibiting equivariance to patch-wise translation and 360-rotation. We achieve this by replacing regular CNN filters with circular harmonics, returning a maximal response and orientation for every receptive field patch. H-Nets use a rich, parameter-efficient and low computational complexity representation, and we show that deep feature maps within the network encode complicated rotational invariants. We demonstrate that our layers are general enough to be used in conjunction with the latest architectures and techniques, such as deep supervision and batch normalization. We also achieve state-of-the-art classification on rotated-MNIST, and competitive results on other benchmark challenges.