Behind the Scenes: Density Fields for Single View Reconstruction

Inferring a meaningful geometric scene representation from a single image is a fundamental problem in computer vision. Approaches based on traditional depth map prediction can only reason about areas that are visible in the image. Currently, neural radiance fields (NeRFs) can capture true 3D including color but are too complex to be generated from a single image. As an alternative, we introduce a neural network that predicts an implicit density field from a single image. It maps every location in the frustum of the image to volumetric density. Our network can be trained through self-supervision from only video data. By not storing color in the implicit volume, but directly sampling color from the available views during training, our scene representation becomes significantly less complex compared to NeRFs, and we can train neural networks to predict it. Thus, we can apply volume rendering to perform both depth prediction and novel view synthesis. In our experiments, we show that our method is able to predict meaningful geometry for regions that are occluded in the input image. Additionally, we demonstrate the potential of our approach on three datasets for depth prediction and novel-view synthesis.

Multi-Vehicle Trajectory Prediction at Intersections using State and Intention Information

Traditional approaches to prediction of future trajectory of road agents rely on knowing information about their past trajectory. This work rather relies only on having knowledge of the current state and intended direction to make predictions for multiple vehicles at intersections. Furthermore, message passing of this information between the vehicles provides each one of them a more holistic overview of the environment allowing for a more informed prediction. This is done by training a neural network which takes the state and intent of the multiple vehicles to predict their future trajectory. Using the intention as an input allows our approach to be extended to additionally control the multiple vehicles to drive towards desired paths. Experimental results demonstrate the robustness of our approach both in terms of trajectory prediction and vehicle control at intersections. The complete training and evaluation code for this work is available here: \url{https://github.com/Dekai21/Multi_Agent_Intersection}.

4Seasons: Benchmarking Visual SLAM and Long-Term Localization for Autonomous Driving in Challenging Conditions

In this paper, we present a novel visual SLAM and long-term localization benchmark for autonomous driving in challenging conditions based on the large-scale 4Seasons dataset. The proposed benchmark provides drastic appearance variations caused by seasonal changes and diverse weather and illumination conditions. While significant progress has been made in advancing visual SLAM on small-scale datasets with similar conditions, there is still a lack of unified benchmarks representative of real-world scenarios for autonomous driving. We introduce a new unified benchmark for jointly evaluating visual odometry, global place recognition, and map-based visual localization performance which is crucial to successfully enable autonomous driving in any condition. The data has been collected for more than one year, resulting in more than 300 km of recordings in nine different environments ranging from a multi-level parking garage to urban (including tunnels) to countryside and highway. We provide globally consistent reference poses with up to centimeter-level accuracy obtained from the fusion of direct stereo-inertial odometry with RTK GNSS. We evaluate the performance of several state-of-the-art visual odometry and visual localization baseline approaches on the benchmark and analyze their properties. The experimental results provide new insights into current approaches and show promising potential for future research. Our benchmark and evaluation protocols will be available at https://www.4seasons-dataset.com/.

Masked Event Modeling: Self-Supervised Pretraining for Event Cameras

Event cameras offer the capacity to asynchronously capture brightness changes with low latency, high temporal resolution, and high dynamic range. Deploying deep learning methods for classification or other tasks to these sensors typically requires large labeled datasets. Since the amount of labeled event data is tiny compared to the bulk of labeled RGB imagery, the progress of event-based vision has remained limited. To reduce the dependency on labeled event data, we introduce Masked Event Modeling (MEM), a self-supervised pretraining framework for events. Our method pretrains a neural network on unlabeled events, which can originate from any event camera recording. Subsequently, the pretrained model is finetuned on a downstream task leading to an overall better performance while requiring fewer labels. Our method outperforms the state-of-the-art on N-ImageNet, N-Cars, and N-Caltech101, increasing the object classification accuracy on N-ImageNet by 7.96%. We demonstrate that Masked Event Modeling is superior to RGB-based pretraining on a real world dataset.

SupeRVol: Super-Resolution Shape and Reflectance Estimation in Inverse Volume Rendering

We propose an end-to-end inverse rendering pipeline called SupeRVol that allows us to recover 3D shape and material parameters from a set of color images in a super-resolution manner. To this end, we represent both the bidirectional reflectance distribution function (BRDF) and the signed distance function (SDF) by multi-layer perceptrons. In order to obtain both the surface shape and its reflectance properties, we revert to a differentiable volume renderer with a physically based illumination model that allows us to decouple reflectance and lighting. This physical model takes into account the effect of the camera's point spread function thereby enabling a reconstruction of shape and material in a super-resolution quality. Experimental validation confirms that SupeRVol achieves state of the art performance in terms of inverse rendering quality. It generates reconstructions that are sharper than the individual input images, making this method ideally suited for 3D modeling from low-resolution imagery.

PRISM: Probabilistic Real-Time Inference in Spatial World Models

We introduce PRISM, a method for real-time filtering in a probabilistic generative model of agent motion and visual perception. Previous approaches either lack uncertainty estimates for the map and agent state, do not run in real-time, do not have a dense scene representation or do not model agent dynamics. Our solution reconciles all of these aspects. We start from a predefined state-space model which combines differentiable rendering and 6-DoF dynamics. Probabilistic inference in this model amounts to simultaneous localisation and mapping (SLAM) and is intractable. We use a series of approximations to Bayesian inference to arrive at probabilistic map and state estimates. We take advantage of well-established methods and closed-form updates, preserving accuracy and enabling real-time capability. The proposed solution runs at 10Hz real-time and is similarly accurate to state-of-the-art SLAM in small to medium-sized indoor environments, with high-speed UAV and handheld camera agents (Blackbird, EuRoC and TUM-RGBD).

G-MSM: Unsupervised Multi-Shape Matching with Graph-based Affinity Priors

We present G-MSM (Graph-based Multi-Shape Matching), a novel unsupervised learning approach for non-rigid shape correspondence. Rather than treating a collection of input poses as an unordered set of samples, we explicitly model the underlying shape data manifold. To this end, we propose an adaptive multi-shape matching architecture that constructs an affinity graph on a given set of training shapes in a self-supervised manner. The key idea is to combine putative, pairwise correspondences by propagating maps along shortest paths in the underlying shape graph. During training, we enforce cycle-consistency between such optimal paths and the pairwise matches which enables our model to learn topology-aware shape priors. We explore different classes of shape graphs and recover specific settings, like template-based matching (star graph) or learnable ranking/sorting (TSP graph), as special cases in our framework. Finally, we demonstrate state-of-the-art performance on several recent shape correspondence benchmarks, including real-world 3D scan meshes with topological noise and challenging inter-class pairs.

PVT3D: Point Voxel Transformers for Place Recognition from Sparse Lidar Scans

Place recognition based on point cloud (LiDAR) scans is an important module for achieving robust autonomy in robots or self-driving vehicles. Training deep networks to match such scans presents a difficult trade-off: a higher spatial resolution of the network's intermediate representations is needed to perform fine-grained matching of subtle geometric features, but growing it too large makes the memory requirements infeasible. In this work, we propose a Point-Voxel Transformer network (PVT3D) that achieves robust fine-grained matching with low memory requirements. It leverages a sparse voxel branch to extract and aggregate information at a lower resolution and a point-wise branch to obtain fine-grained local information. A novel hierarchical cross-attention transformer (HCAT) uses queries from one branch to try to match structures in the other branch, ensuring that both extract self-contained descriptors of the point cloud (rather than one branch dominating), but using both to inform the output global descriptor of the point cloud. Extensive experiments show that the proposed PVT3D method surpasses the state-of-the-art by a large amount on several datasets (Oxford RobotCar, TUM, USyd). For instance, we achieve AR@1 of 85.6% on the TUM dataset, which surpasses the strongest prior model by ~15%.

A Graph Is More Than Its Nodes: Towards Structured Uncertainty-Aware Learning on Graphs

Current graph neural networks (GNNs) that tackle node classification on graphs tend to only focus on nodewise scores and are solely evaluated by nodewise metrics. This limits uncertainty estimation on graphs since nodewise marginals do not fully characterize the joint distribution given the graph structure. In this work, we propose novel edgewise metrics, namely the edgewise expected calibration error (ECE) and the agree/disagree ECEs, which provide criteria for uncertainty estimation on graphs beyond the nodewise setting. Our experiments demonstrate that the proposed edgewise metrics can complement the nodewise results and yield additional insights. Moreover, we show that GNN models which consider the structured prediction problem on graphs tend to have better uncertainty estimations, which illustrates the benefit of going beyond the nodewise setting.

What Makes Graph Neural Networks Miscalibrated?

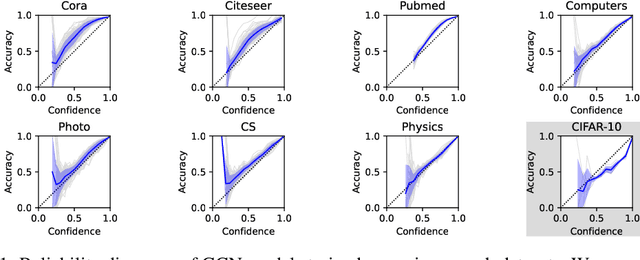
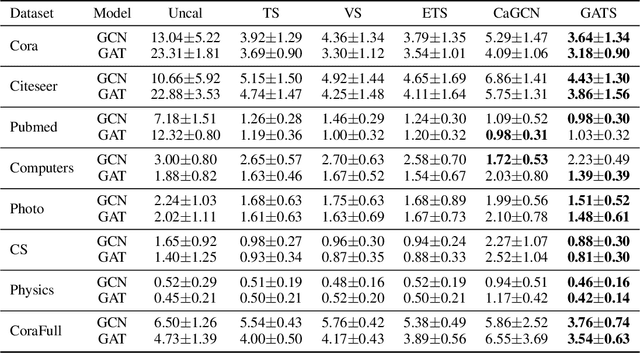
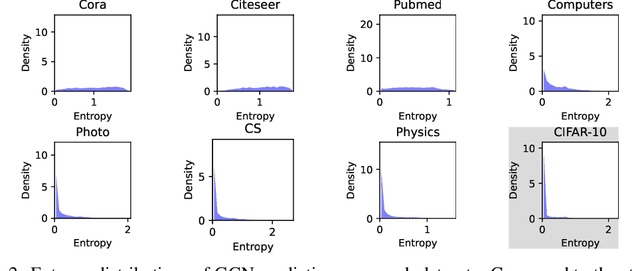
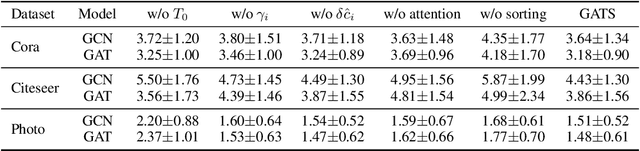
Given the importance of getting calibrated predictions and reliable uncertainty estimations, various post-hoc calibration methods have been developed for neural networks on standard multi-class classification tasks. However, these methods are not well suited for calibrating graph neural networks (GNNs), which presents unique challenges such as accounting for the graph structure and the graph-induced correlations between the nodes. In this work, we conduct a systematic study on the calibration qualities of GNN node predictions. In particular, we identify five factors which influence the calibration of GNNs: general under-confident tendency, diversity of nodewise predictive distributions, distance to training nodes, relative confidence level, and neighborhood similarity. Furthermore, based on the insights from this study, we design a novel calibration method named Graph Attention Temperature Scaling (GATS), which is tailored for calibrating graph neural networks. GATS incorporates designs that address all the identified influential factors and produces nodewise temperature scaling using an attention-based architecture. GATS is accuracy-preserving, data-efficient, and expressive at the same time. Our experiments empirically verify the effectiveness of GATS, demonstrating that it can consistently achieve state-of-the-art calibration results on various graph datasets for different GNN backbones.