An Exhaustive DPLL Approach to Model Counting over Integer Linear Constraints with Simplification Techniques

Linear constraints are one of the most fundamental constraints in fields such as computer science, operations research and optimization. Many applications reduce to the task of model counting over integer linear constraints (MCILC). In this paper, we design an exact approach to MCILC based on an exhaustive DPLL architecture. To improve the efficiency, we integrate several effective simplification techniques from mixed integer programming into the architecture. We compare our approach to state-of-the-art MCILC counters and propositional model counters on 2840 random and 4131 application benchmarks. Experimental results show that our approach significantly outperforms all exact methods in random benchmarks solving 1718 instances while the state-of-the-art approach only computes 1470 instances. In addition, our approach is the only approach to solve all 4131 application instances.

Curriculum Abductive Learning

Abductive Learning (ABL) integrates machine learning with logical reasoning in a loop: a learning model predicts symbolic concept labels from raw inputs, which are revised through abduction using domain knowledge and then fed back for retraining. However, due to the nondeterminism of abduction, the training process often suffers from instability, especially when the knowledge base is large and complex, resulting in a prohibitively large abduction space. While prior works focus on improving candidate selection within this space, they typically treat the knowledge base as a static black box. In this work, we propose Curriculum Abductive Learning (C-ABL), a method that explicitly leverages the internal structure of the knowledge base to address the ABL training challenges. C-ABL partitions the knowledge base into a sequence of sub-bases, progressively introduced during training. This reduces the abduction space throughout training and enables the model to incorporate logic in a stepwise, smooth way. Experiments across multiple tasks show that C-ABL outperforms previous ABL implementations, significantly improves training stability, convergence speed, and final accuracy, especially under complex knowledge setting.

Approximate Integer Solution Counts over Linear Arithmetic Constraints

Counting integer solutions of linear constraints has found interesting applications in various fields. It is equivalent to the problem of counting lattice points inside a polytope. However, state-of-the-art algorithms for this problem become too slow for even a modest number of variables. In this paper, we propose a new framework to approximate the lattice counts inside a polytope with a new random-walk sampling method. The counts computed by our approach has been proved approximately bounded by a $(\epsilon, \delta)$-bound. Experiments on extensive benchmarks show that our algorithm could solve polytopes with dozens of dimensions, which significantly outperforms state-of-the-art counters.

Counting the Number of Solutions to Constraints

Compared with constraint satisfaction problems, counting problems have received less attention. In this paper, we survey research works on the problems of counting the number of solutions to constraints. The constraints may take various forms, including, formulas in the propositional logic, linear inequalities over the reals or integers, Boolean combination of linear constraints. We describe some techniques and tools for solving the counting problems, as well as some applications (e.g., applications to automated reasoning, program analysis, formal verification and information security).

A New Probabilistic Algorithm for Approximate Model Counting

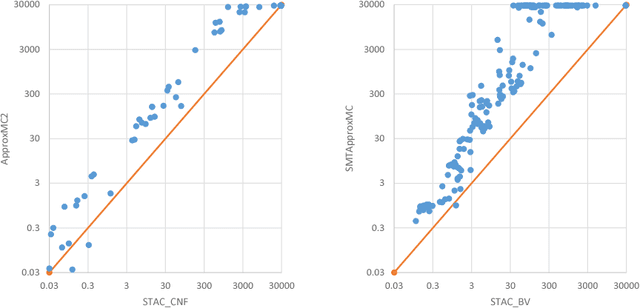
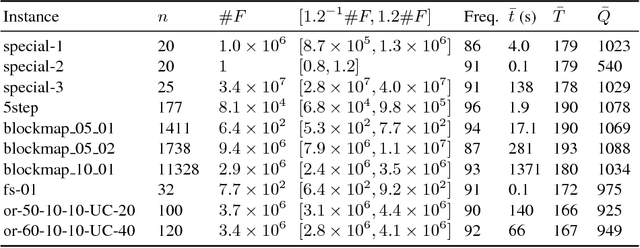
Constrained counting is important in domains ranging from artificial intelligence to software analysis. There are already a few approaches for counting models over various types of constraints. Recently, hashing-based approaches achieve both theoretical guarantees and scalability, but still rely on solution enumeration. In this paper, a new probabilistic polynomial time approximate model counter is proposed, which is also a hashing-based universal framework, but with only satisfiability queries. A variant with a dynamic stopping criterion is also presented. Empirical evaluation over benchmarks on propositional logic formulas and SMT(BV) formulas shows that the approach is promising.

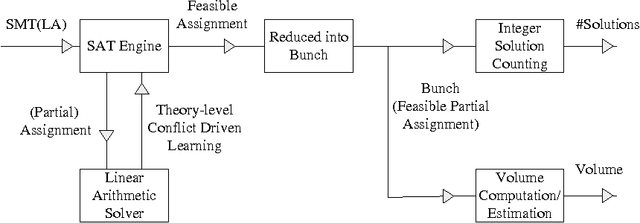
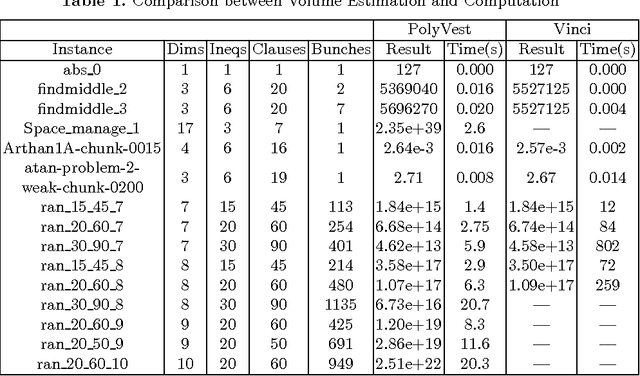
A Tool for Computing and Estimating the Volume of the Solution Space of SMT

There are already quite a few tools for solving the Satisfiability Modulo Theories (SMT) problems. In this paper, we present \texttt{VolCE}, a tool for counting the solutions of SMT constraints, or in other words, for computing the volume of the solution space. Its input is essentially a set of Boolean combinations of linear constraints, where the numeric variables are either all integers or all reals, and each variable is bounded. The tool extends SMT solving with integer solution counting and volume computation/estimation for convex polytopes. Effective heuristics are adopted, which enable the tool to deal with high-dimensional problem instances efficiently and accurately.