Weight-Space Physics: Interpretable Hypernetworks for Lattice Quantum Field Theories

Lattice field theory is the workhorse of non-perturbative physics, used to simulate phenomena from the strong nuclear force to critical phenomena in materials. Its Boltzmann distributions are parametrized analytically by coupling constants, but these bare parameters are weak predictors of observables -- extracting physics typically requires extensive simulation. While normalizing flows have emerged as effective samplers at fixed couplings, it remains difficult to interpret what these networks have learned. This raises a natural question: can the physics be read off directly from the flow network parameters themselves, and can those parameters be generated for unseen theories? We propose lattice field theory as a testbed for neural network interpretability: because the target physics is qualitatively well-understood and smoothly varying, it provides ideal synthetic data with known ground truth. To this end, we introduce JEPAWG, a Joint-Embedding Predictive Architecture-based Weight Generator that maps couplings directly to flow weights via a learned latent space. On a scalar theory at lattices of size $6^2$ to $11^2$, the JEPAWG latent space recovers the correct intrinsic dimension of the underlying manifold, locates the phase transition, and encodes a finite-size shift aligned with the 2D Ising exponent $ν\approx 1$, allowing us to uncover physical structure by studying the network weights alone. This suggests the fascinating idea of treating the network weights as a new type of physical observable. As a generator, JEPAWG also interpolates and extrapolates to unseen couplings effectively and remains robust to weight-space discontinuities introduced by multi-seed training data, outperforming PCA, AE, and VAE baselines.

Analytic Bijections for Smooth and Interpretable Normalizing Flows

A key challenge in designing normalizing flows is finding expressive scalar bijections that remain invertible with tractable Jacobians. Existing approaches face trade-offs: affine transformations are smooth and analytically invertible but lack expressivity; monotonic splines offer local control but are only piecewise smooth and act on bounded domains; residual flows achieve smoothness but need numerical inversion. We introduce three families of analytic bijections -- cubic rational, sinh, and cubic polynomial -- that are globally smooth ($C^\infty$), defined on all of $\mathbb{R}$, and analytically invertible in closed form, combining the favorable properties of all prior approaches. These bijections serve as drop-in replacements in coupling flows, matching or exceeding spline performance. Beyond coupling layers, we develop radial flows: a novel architecture using direct parametrization that transforms the radial coordinate while preserving angular direction. Radial flows exhibit exceptional training stability, produce geometrically interpretable transformations, and on targets with radial structure can achieve comparable quality to coupling flows with $1000\times$ fewer parameters. We provide comprehensive evaluation on 1D and 2D benchmarks, and demonstrate applicability to higher-dimensional physics problems through experiments on $φ^4$ lattice field theory, where our bijections outperform affine baselines and enable problem-specific designs that address mode collapse.

Continuous normalizing flows for lattice gauge theories

Continuous normalizing flows are known to be highly expressive and flexible, which allows for easier incorporation of large symmetries and makes them a powerful tool for sampling in lattice field theories. Building on previous work, we present a general continuous normalizing flow architecture for matrix Lie groups that is equivariant under group transformations. We apply this to lattice gauge theories in two dimensions as a proof-of-principle and demonstrate competitive performance, showing its potential as a tool for future lattice sampling tasks.

GUD: Generation with Unified Diffusion

Diffusion generative models transform noise into data by inverting a process that progressively adds noise to data samples. Inspired by concepts from the renormalization group in physics, which analyzes systems across different scales, we revisit diffusion models by exploring three key design aspects: 1) the choice of representation in which the diffusion process operates (e.g. pixel-, PCA-, Fourier-, or wavelet-basis), 2) the prior distribution that data is transformed into during diffusion (e.g. Gaussian with covariance $\Sigma$), and 3) the scheduling of noise levels applied separately to different parts of the data, captured by a component-wise noise schedule. Incorporating the flexibility in these choices, we develop a unified framework for diffusion generative models with greatly enhanced design freedom. In particular, we introduce soft-conditioning models that smoothly interpolate between standard diffusion models and autoregressive models (in any basis), conceptually bridging these two approaches. Our framework opens up a wide design space which may lead to more efficient training and data generation, and paves the way to novel architectures integrating different generative approaches and generation tasks.

Learning Lattice Quantum Field Theories with Equivariant Continuous Flows

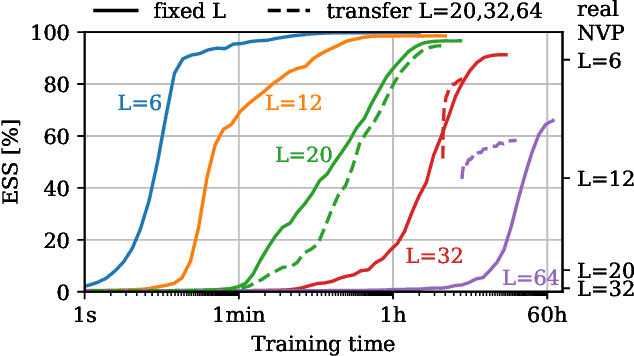
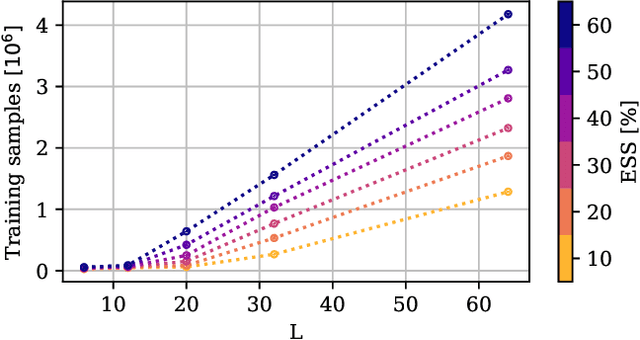
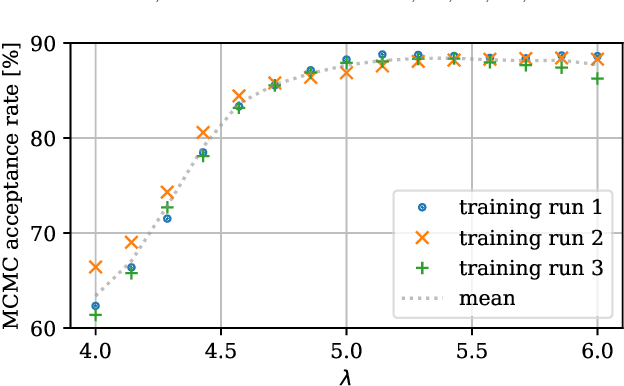
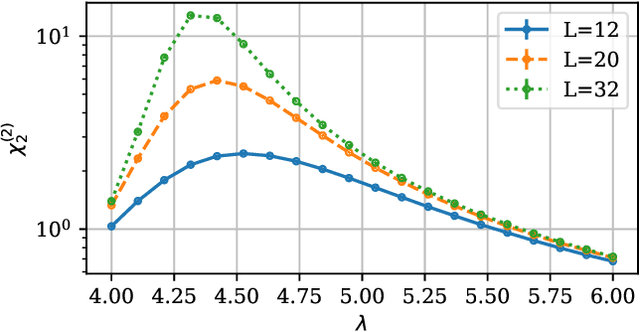
We propose a novel machine learning method for sampling from the high-dimensional probability distributions of Lattice Quantum Field Theories. Instead of the deep architectures used so far for this task, our proposal is based on a single neural ODE layer and incorporates the full symmetries of the problem. We test our model on the $\phi^4$ theory, showing that it systematically outperforms previously proposed flow-based methods in sampling efficiency, and the improvement is especially pronounced for larger lattices. Compared to the previous baseline model, we improve a key metric, the effective sample size, from 1% to 91% on a lattice of size $32\times 32$. We also demonstrate that our model can successfully learn a continuous family of theories at once, and the results of learning can be transferred to larger lattices. Such generalization capacities further accentuate the potential advantages of machine learning methods compared to traditional MCMC-based methods.