Noise Is Not the Main Factor Behind the Gap Between SGD and Adam on Transformers, but Sign Descent Might Be

The success of the Adam optimizer on a wide array of architectures has made it the default in settings where stochastic gradient descent (SGD) performs poorly. However, our theoretical understanding of this discrepancy is lagging, preventing the development of significant improvements on either algorithm. Recent work advances the hypothesis that Adam and other heuristics like gradient clipping outperform SGD on language tasks because the distribution of the error induced by sampling has heavy tails. This suggests that Adam outperform SGD because it uses a more robust gradient estimate. We evaluate this hypothesis by varying the batch size, up to the entire dataset, to control for stochasticity. We present evidence that stochasticity and heavy-tailed noise are not major factors in the performance gap between SGD and Adam. Rather, Adam performs better as the batch size increases, while SGD is less effective at taking advantage of the reduction in noise. This raises the question as to why Adam outperforms SGD in the full-batch setting. Through further investigation of simpler variants of SGD, we find that the behavior of Adam with large batches is similar to sign descent with momentum.

Fast Sparse Decision Tree Optimization via Reference Ensembles

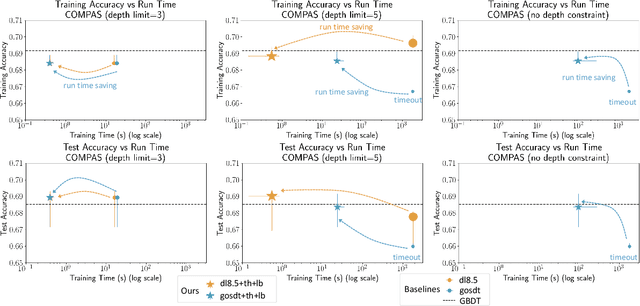
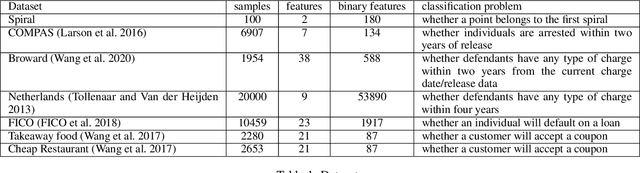
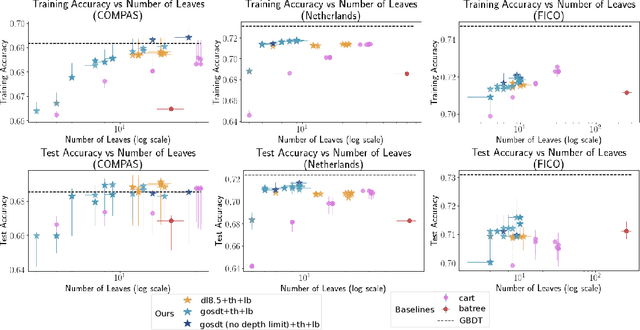
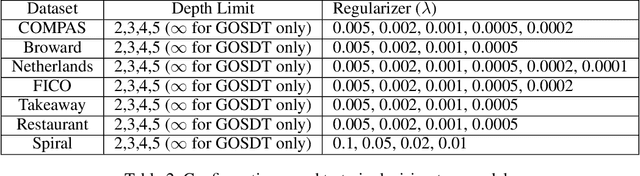
Sparse decision tree optimization has been one of the most fundamental problems in AI since its inception and is a challenge at the core of interpretable machine learning. Sparse decision tree optimization is computationally hard, and despite steady effort since the 1960's, breakthroughs have only been made on the problem within the past few years, primarily on the problem of finding optimal sparse decision trees. However, current state-of-the-art algorithms often require impractical amounts of computation time and memory to find optimal or near-optimal trees for some real-world datasets, particularly those having several continuous-valued features. Given that the search spaces of these decision tree optimization problems are massive, can we practically hope to find a sparse decision tree that competes in accuracy with a black box machine learning model? We address this problem via smart guessing strategies that can be applied to any optimal branch-and-bound-based decision tree algorithm. We show that by using these guesses, we can reduce the run time by multiple orders of magnitude, while providing bounds on how far the resulting trees can deviate from the black box's accuracy and expressive power. Our approach enables guesses about how to bin continuous features, the size of the tree, and lower bounds on the error for the optimal decision tree. Our experiments show that in many cases we can rapidly construct sparse decision trees that match the accuracy of black box models. To summarize: when you are having trouble optimizing, just guess.