On Learning-Curve Monotonicity for Maximum Likelihood Estimators

The property of learning-curve monotonicity, highlighted in a recent series of work by Loog, Mey and Viering, describes algorithms which only improve in average performance given more data, for any underlying data distribution within a given family. We establish the first nontrivial monotonicity guarantees for the maximum likelihood estimator in a variety of well-specified parametric settings. For sequential prediction with log loss, we show monotonicity (in fact complete monotonicity) of the forward KL divergence for Gaussian vectors with unknown covariance and either known or unknown mean, as well as for Gamma variables with unknown scale parameter. The Gaussian setting was explicitly highlighted as open in the aforementioned works, even in dimension 1. Finally we observe that for reverse KL divergence, a folklore trick yields monotonicity for very general exponential families. All results in this paper were derived by variants of GPT-5.2 Pro. Humans did not provide any proof strategies or intermediate arguments, but only prompted the model to continue developing additional results, and verified and transcribed its proofs.

Online Allocation and Learning in the Presence of Strategic Agents

We study the problem of allocating $T$ sequentially arriving items among $n$ homogeneous agents under the constraint that each agent must receive a pre-specified fraction of all items, with the objective of maximizing the agents' total valuation of items allocated to them. The agents' valuations for the item in each round are assumed to be i.i.d. but their distribution is a priori unknown to the central planner. Therefore, the central planner needs to implicitly learn these distributions from the observed values in order to pick a good allocation policy. However, an added challenge here is that the agents are strategic with incentives to misreport their valuations in order to receive better allocations. This sets our work apart both from the online auction design settings which typically assume known valuation distributions and/or involve payments, and from the online learning settings that do not consider strategic agents. To that end, our main contribution is an online learning based allocation mechanism that is approximately Bayesian incentive compatible, and when all agents are truthful, guarantees a sublinear regret for individual agents' utility compared to that under the optimal offline allocation policy.

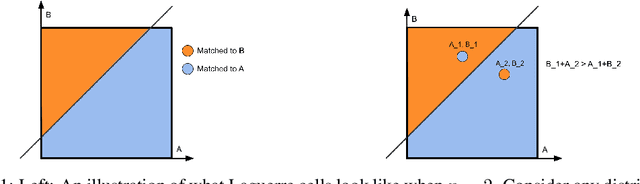
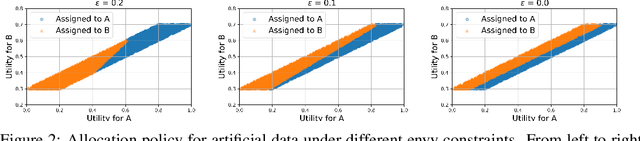
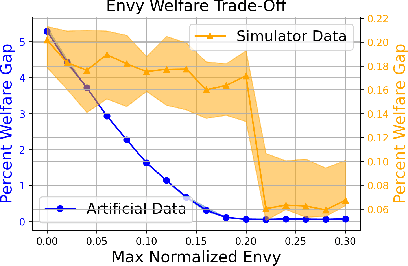
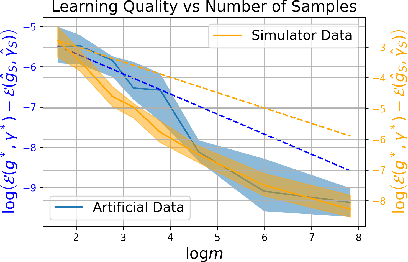
Optimal Efficiency-Envy Trade-Off via Optimal Transport

We consider the problem of allocating a distribution of items to $n$ recipients where each recipient has to be allocated a fixed, prespecified fraction of all items, while ensuring that each recipient does not experience too much envy. We show that this problem can be formulated as a variant of the semi-discrete optimal transport (OT) problem, whose solution structure in this case has a concise representation and a simple geometric interpretation. Unlike existing literature that treats envy-freeness as a hard constraint, our formulation allows us to \emph{optimally} trade off efficiency and envy continuously. Additionally, we study the statistical properties of the space of our OT based allocation policies by showing a polynomial bound on the number of samples needed to approximate the optimal solution from samples. Our approach is suitable for large-scale fair allocation problems such as the blood donation matching problem, and we show numerically that it performs well on a prior realistic data simulator.

Dynamic Pricing and Learning under the Bass Model

We consider a novel formulation of the dynamic pricing and demand learning problem, where the evolution of demand in response to posted prices is governed by a stochastic variant of the popular Bass model with parameters $\alpha, \beta$ that are linked to the so-called "innovation" and "imitation" effects. Unlike the more commonly used i.i.d. and contextual demand models, in this model the posted price not only affects the demand and the revenue in the current round but also the future evolution of demand, and hence the fraction of potential market size $m$ that can be ultimately captured. In this paper, we consider the more challenging incomplete information problem where dynamic pricing is applied in conjunction with learning the unknown parameters, with the objective of optimizing the cumulative revenues over a given selling horizon of length $T$. Equivalently, the goal is to minimize the regret which measures the revenue loss of the algorithm relative to the optimal expected revenue achievable under the stochastic Bass model with market size $m$ and time horizon $T$. Our main contribution is the development of an algorithm that satisfies a high probability regret guarantee of order $\tilde O(m^{2/3})$; where the market size $m$ is known a priori. Moreover, we show that no algorithm can incur smaller order of loss by deriving a matching lower bound. Unlike most regret analysis results, in the present problem the market size $m$ is the fundamental driver of the complexity; our lower bound in fact, indicates that for any fixed $\alpha, \beta$, most non-trivial instances of the problem have constant $T$ and large $m$. We believe that this insight sets the problem of dynamic pricing under the Bass model apart from the typical i.i.d. setting and multi-armed bandit based models for dynamic pricing, which typically focus only on the asymptotics with respect to time horizon $T$.