Adaptivity and Confounding in Multi-Armed Bandit Experiments

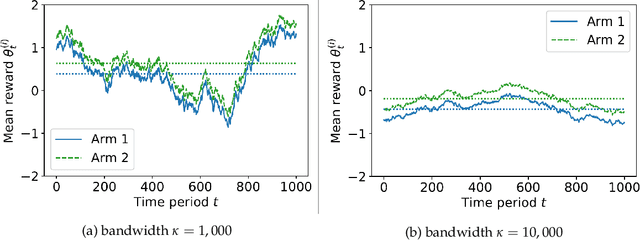
We explore a new model of bandit experiments where a potentially nonstationary sequence of contexts influences arms' performance. Context-unaware algorithms risk confounding while those that perform correct inference face information delays. Our main insight is that an algorithm we call deconfounted Thompson sampling strikes a delicate balance between adaptivity and robustness. Its adaptivity leads to optimal efficiency properties in easy stationary instances, but it displays surprising resilience in hard nonstationary ones which cause other adaptive algorithms to fail.

An Analysis of Ensemble Sampling

Ensemble sampling serves as a practical approximation to Thompson sampling when maintaining an exact posterior distribution over model parameters is computationally intractable. In this paper, we establish a Bayesian regret bound that ensures desirable behavior when ensemble sampling is applied to the linear bandit problem. This represents the first rigorous regret analysis of ensemble sampling and is made possible by leveraging information-theoretic concepts and novel analytic techniques that may prove useful beyond the scope of this paper.

Best Arm Identification with a Fixed Budget under a Small Gap

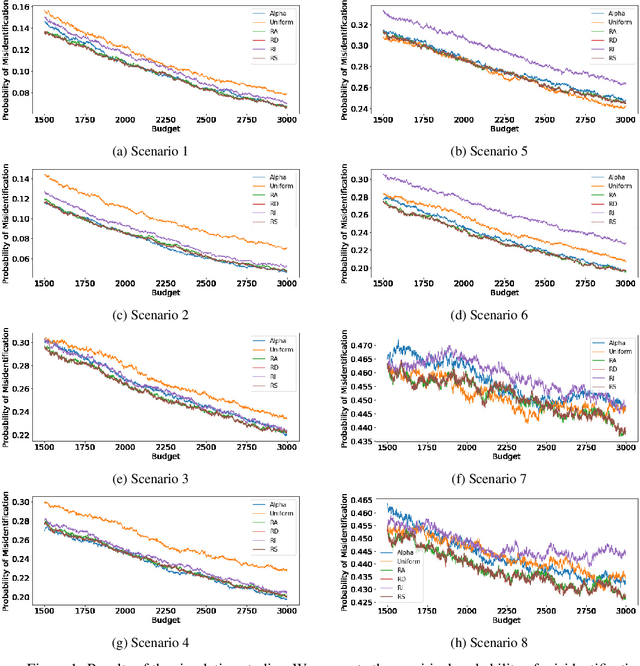
We consider the fixed-budget best arm identification problem in the multi-armed bandit problem. One of the main interests in this field is to derive a tight lower bound on the probability of misidentifying the best arm and to develop a strategy whose performance guarantee matches the lower bound. However, it has long been an open problem when the optimal allocation ratio of arm draws is unknown. In this paper, we provide an answer for this problem under which the gap between the expected rewards is small. First, we derive a tight problem-dependent lower bound, which characterizes the optimal allocation ratio that depends on the gap of the expected rewards and the Fisher information of the bandit model. Then, we propose the "RS-AIPW" strategy, which consists of the randomized sampling (RS) rule using the estimated optimal allocation ratio and the recommendation rule using the augmented inverse probability weighting (AIPW) estimator. Our proposed strategy is optimal in the sense that the performance guarantee achieves the derived lower bound under a small gap. In the course of the analysis, we present a novel large deviation bound for martingales.

Optimal Simple Regret in Bayesian Best Arm Identification

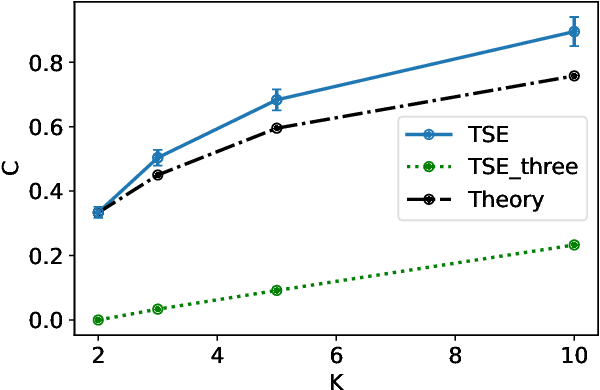
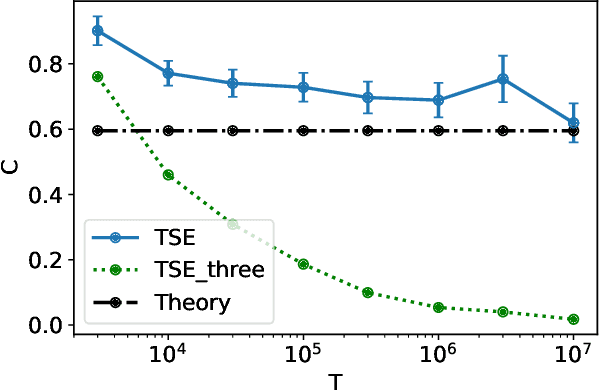
We consider Bayesian best arm identification in the multi-armed bandit problem. Assuming certain continuity conditions of the prior, we characterize the rate of the Bayesian simple regret. Differing from Bayesian regret minimization (Lai, 1987), the leading factor in Bayesian simple regret derives from the region where the gap between optimal and sub-optimal arms is smaller than $\sqrt{\frac{\log T}{T}}$. We propose a simple and easy-to-compute algorithm with its leading factor matches with the lower bound up to a constant factor; simulation results support our theoretical findings.

Policy Choice and Best Arm Identification: Comments on "Adaptive Treatment Assignment in Experiments for Policy Choice"

Adaptive experimental design for efficient decision-making is an important problem in economics. The purpose of this paper is to connect the "policy choice" problem, proposed in Kasy and Sautmann (2021) as an instance of adaptive experimental design, to the frontiers of the bandit literature in machine learning. We discuss how the policy choice problem can be framed in a way such that it is identical to what is called the "best arm identification" (BAI) problem. By connecting the literature, we identify that the asymptotic optimality of policy choice algorithms tackled in Kasy and Sautmann (2021) is a long-standing open question in the literature. While Kasy and Sautmann (2021) presents an interesting and important empirical study, unfortunately, this connection highlights several major issues with the theoretical results. In particular, we show that Theorem 1 in Kasy and Sautmann (2021) is false. We find that the proofs of statements (1) and (2) of Theorem 1 are incorrect. Although the statements themselves may be true, they are non-trivial to fix. Statement (3), and its proof, on the other hand, is false, which we show by utilizing existing theoretical results in the bandit literature. As this question is critically important, garnering much interest in the last decade within the bandit community, we provide a review of recent developments in the BAI literature. We hope this serves to highlight the relevance to economic problems and stimulate methodological and theoretical developments in the econometric community.

PCVPC: Perception Constrained Visual Predictive Control For Agile Quadrotors

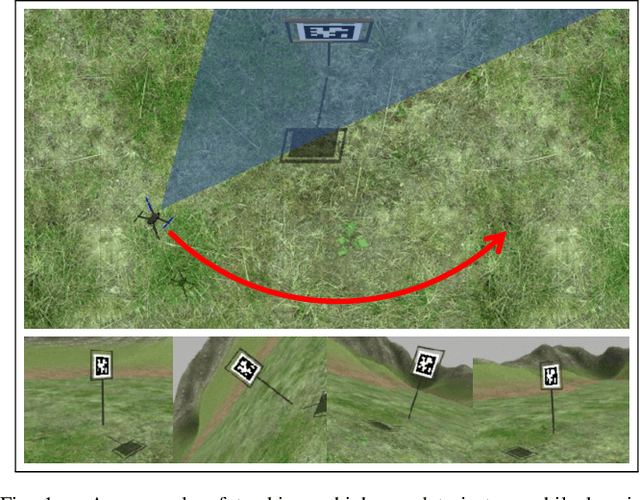
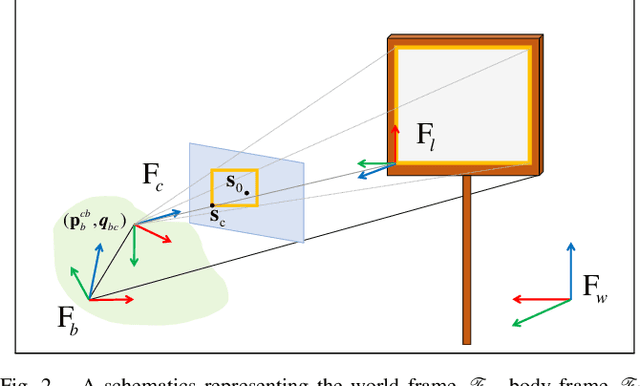
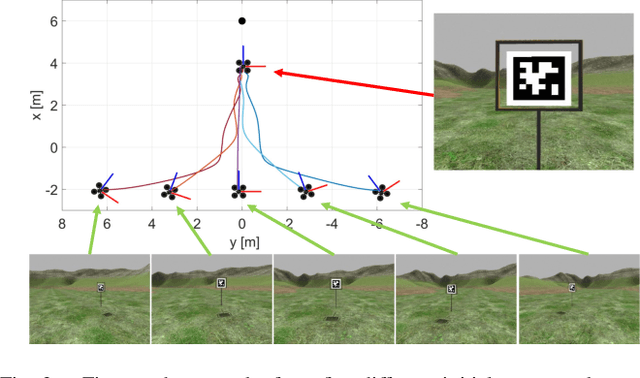
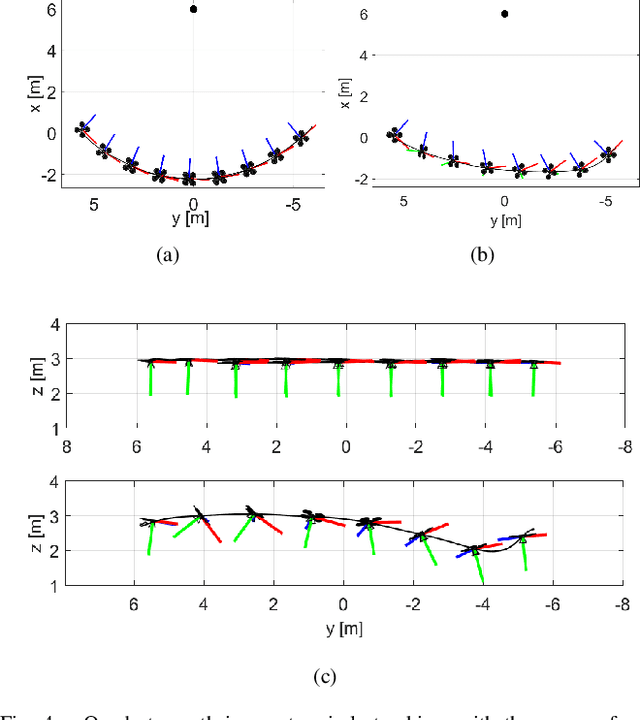
We present a perception constrained visual predictive control (PCVPC) algorithm for quadrotors to enable aggressive flights without using any position information. Our framework leverages nonlinear model predictive control (NMPC) to formulate a constrained image-based visual servoing (IBVS) problem. The quadrotor dynamics, image dynamics, actuation constraints, and visibility constraints are taken into account to handle quadrotor maneuvers with high agility. Two main challenges of applying IBVS to agile drones are considered: (i) high sensitivity of depths to intense orientation changes, and (ii) conflict between the visual servoing objective and action objective due to the underactuated nature. To deal with the first challenge, we parameterize a visual feature by a bearing vector and a distance, by which the depth will no longer be involved in the image dynamics. Meanwhile, we settle the conflict problem by compensating for the rotation in the future visual servoing cost using the predicted orientations of the quadrotor. Our approach in simulation shows that (i) it can work without any position information, (ii) it can achieve a maximum referebce speed of 9 m/s in trajectory tracking without losing the target, and (iii) it can reach a landmark, e.g., a gate in drone racing, from varied initial configurations.

LINS: A Lidar-Inerital State Estimator for Robust and Fast Navigation

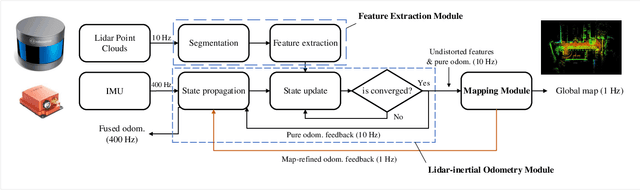
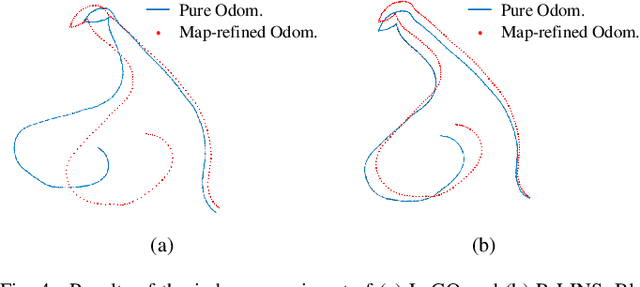
Robust and fast ego-motion estimation is a critical problem for autonomous robots. With high reliability and precision, 3D-lidar-based simultaneous localization and mapping (SLAM) has been widely used in the robotics community to solve this problem. However, the lidar alone is not enough to provide full autonomy to robot navigation in terms of robustness and operating scope, especially in feature-less scenes. In this paper, we present LINS: a lidar-inertial state estimator for robust and fast navigation. Our approach tightly couples the 3D lidar and the inertial measurement unit (IMU) by an iterative error-state Kalman filter (IESKF). To validate generalizability and long-time practicability, extensive experiments are performed in a variety of scenarios including the city, port, forest, and parking lot. The results indicate that LINS outperforms the lidar-only methods in terms of accuracy and it is faster than the state-of-the-art lidar-inertial fusion methods in nearly an order of magnitude.

Improving the Expected Improvement Algorithm

The expected improvement (EI) algorithm is a popular strategy for information collection in optimization under uncertainty. The algorithm is widely known to be too greedy, but nevertheless enjoys wide use due to its simplicity and ability to handle uncertainty and noise in a coherent decision theoretic framework. To provide rigorous insight into EI, we study its properties in a simple setting of Bayesian optimization where the domain consists of a finite grid of points. This is the so-called best-arm identification problem, where the goal is to allocate measurement effort wisely to confidently identify the best arm using a small number of measurements. In this framework, one can show formally that EI is far from optimal. To overcome this shortcoming, we introduce a simple modification of the expected improvement algorithm. Surprisingly, this simple change results in an algorithm that is asymptotically optimal for Gaussian best-arm identification problems, and provably outperforms standard EI by an order of magnitude.