Principal Component Projection Without Principal Component Analysis

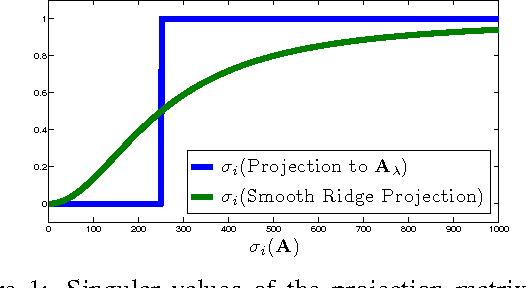
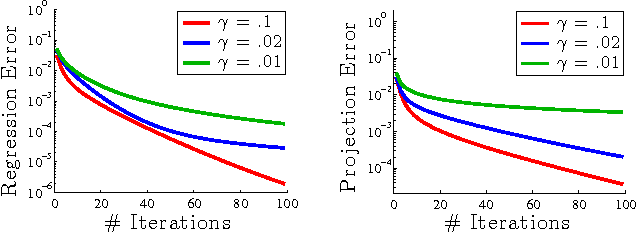
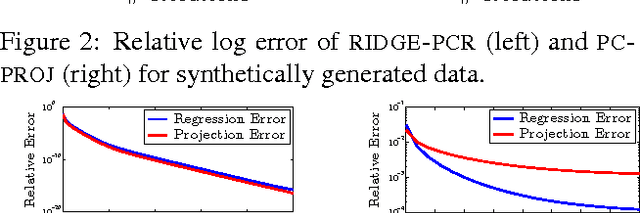
We show how to efficiently project a vector onto the top principal components of a matrix, without explicitly computing these components. Specifically, we introduce an iterative algorithm that provably computes the projection using few calls to any black-box routine for ridge regression. By avoiding explicit principal component analysis (PCA), our algorithm is the first with no runtime dependence on the number of top principal components. We show that it can be used to give a fast iterative method for the popular principal component regression problem, giving the first major runtime improvement over the naive method of combining PCA with regression. To achieve our results, we first observe that ridge regression can be used to obtain a "smooth projection" onto the top principal components. We then sharpen this approximation to true projection using a low-degree polynomial approximation to the matrix step function. Step function approximation is a topic of long-term interest in scientific computing. We extend prior theory by constructing polynomials with simple iterative structure and rigorously analyzing their behavior under limited precision.

Randomized Block Krylov Methods for Stronger and Faster Approximate Singular Value Decomposition

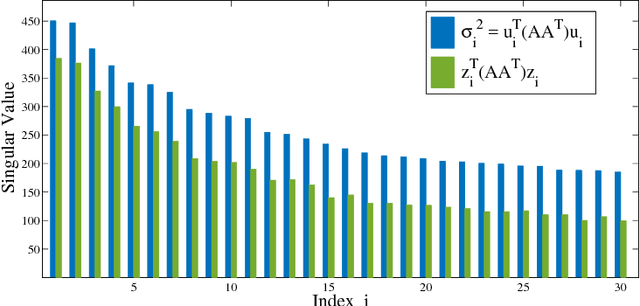
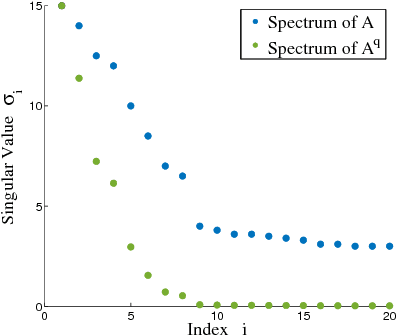
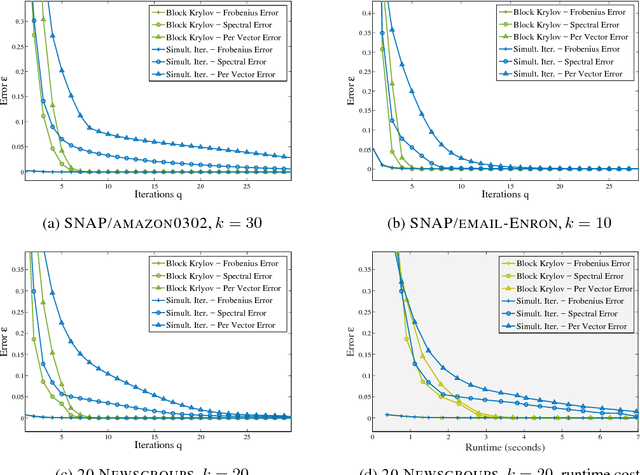
Since being analyzed by Rokhlin, Szlam, and Tygert and popularized by Halko, Martinsson, and Tropp, randomized Simultaneous Power Iteration has become the method of choice for approximate singular value decomposition. It is more accurate than simpler sketching algorithms, yet still converges quickly for any matrix, independently of singular value gaps. After $\tilde{O}(1/\epsilon)$ iterations, it gives a low-rank approximation within $(1+\epsilon)$ of optimal for spectral norm error. We give the first provable runtime improvement on Simultaneous Iteration: a simple randomized block Krylov method, closely related to the classic Block Lanczos algorithm, gives the same guarantees in just $\tilde{O}(1/\sqrt{\epsilon})$ iterations and performs substantially better experimentally. Despite their long history, our analysis is the first of a Krylov subspace method that does not depend on singular value gaps, which are unreliable in practice. Furthermore, while it is a simple accuracy benchmark, even $(1+\epsilon)$ error for spectral norm low-rank approximation does not imply that an algorithm returns high quality principal components, a major issue for data applications. We address this problem for the first time by showing that both Block Krylov Iteration and a minor modification of Simultaneous Iteration give nearly optimal PCA for any matrix. This result further justifies their strength over non-iterative sketching methods. Finally, we give insight beyond the worst case, justifying why both algorithms can run much faster in practice than predicted. We clarify how simple techniques can take advantage of common matrix properties to significantly improve runtime.

Dimensionality Reduction for k-Means Clustering and Low Rank Approximation

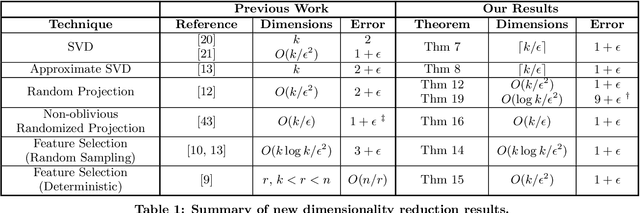
We show how to approximate a data matrix $\mathbf{A}$ with a much smaller sketch $\mathbf{\tilde A}$ that can be used to solve a general class of constrained k-rank approximation problems to within $(1+\epsilon)$ error. Importantly, this class of problems includes $k$-means clustering and unconstrained low rank approximation (i.e. principal component analysis). By reducing data points to just $O(k)$ dimensions, our methods generically accelerate any exact, approximate, or heuristic algorithm for these ubiquitous problems. For $k$-means dimensionality reduction, we provide $(1+\epsilon)$ relative error results for many common sketching techniques, including random row projection, column selection, and approximate SVD. For approximate principal component analysis, we give a simple alternative to known algorithms that has applications in the streaming setting. Additionally, we extend recent work on column-based matrix reconstruction, giving column subsets that not only `cover' a good subspace for $\bv{A}$, but can be used directly to compute this subspace. Finally, for $k$-means clustering, we show how to achieve a $(9+\epsilon)$ approximation by Johnson-Lindenstrauss projecting data points to just $O(\log k/\epsilon^2)$ dimensions. This gives the first result that leverages the specific structure of $k$-means to achieve dimension independent of input size and sublinear in $k$.

Uniform Sampling for Matrix Approximation

Random sampling has become a critical tool in solving massive matrix problems. For linear regression, a small, manageable set of data rows can be randomly selected to approximate a tall, skinny data matrix, improving processing time significantly. For theoretical performance guarantees, each row must be sampled with probability proportional to its statistical leverage score. Unfortunately, leverage scores are difficult to compute. A simple alternative is to sample rows uniformly at random. While this often works, uniform sampling will eliminate critical row information for many natural instances. We take a fresh look at uniform sampling by examining what information it does preserve. Specifically, we show that uniform sampling yields a matrix that, in some sense, well approximates a large fraction of the original. While this weak form of approximation is not enough for solving linear regression directly, it is enough to compute a better approximation. This observation leads to simple iterative row sampling algorithms for matrix approximation that run in input-sparsity time and preserve row structure and sparsity at all intermediate steps. In addition to an improved understanding of uniform sampling, our main proof introduces a structural result of independent interest: we show that every matrix can be made to have low coherence by reweighting a small subset of its rows.