A Linearly Convergent Frank-Wolfe-type Method for Smooth Convex Minimization over the Spectrahedron

We consider the problem of minimizing a smooth and convex function over the $n$-dimensional spectrahedron -- the set of real symmetric $n\times n$ positive semidefinite matrices with unit trace, which underlies numerous applications in statistics, machine learning and additional domains. Standard first-order methods often require high-rank matrix computations which are prohibitive when the dimension $n$ is large. The well-known Frank-Wolfe method on the other hand, only requires efficient rank-one matrix computations, however suffers from worst-case slow convergence, even under conditions that enable linear convergence rates for standard methods. In this work we present the first Frank-Wolfe-based algorithm that only applies efficient rank-one matrix computations and, assuming quadratic growth and strict complementarity conditions, is guaranteed, after a finite number of iterations, to converges linearly, in expectation, and independently of the ambient dimension.

Blackwell's Approachability with Approximation Algorithms

We revisit Blackwell's celebrated approachability problem which considers a repeated vector-valued game between a player and an adversary. Motivated by settings in which the action set of the player or adversary (or both) is difficult to optimize over, for instance when it corresponds to the set of all possible solutions to some NP-Hard optimization problem, we ask what can the player guarantee \textit{efficiently}, when only having access to these sets via approximation algorithms with ratios $\alpha_{\mX} \geq 1$ and $ 1 \geq \alpha_{\mY} > 0$, respectively. Assuming the player has monotone preferences, in the sense that he does not prefer a vector-valued loss $\ell_1$ over $\ell_2$ if $\ell_2 \leq \ell_1$, we establish that given a Blackwell instance with an approachable target set $S$, the downward closure of the appropriately-scaled set $\alpha_{\mX}\alpha_{\mY}^{-1}S$ is \textit{efficiently} approachable with optimal rate. In case only the player's or adversary's set is equipped with an approximation algorithm, we give simpler and more efficient algorithms.

Projection-Free Online Convex Optimization with Time-Varying Constraints

We consider the setting of online convex optimization with adversarial time-varying constraints in which actions must be feasible w.r.t. a fixed constraint set, and are also required on average to approximately satisfy additional time-varying constraints. Motivated by scenarios in which the fixed feasible set (hard constraint) is difficult to project on, we consider projection-free algorithms that access this set only through a linear optimization oracle (LOO). We present an algorithm that, on a sequence of length $T$ and using overall $T$ calls to the LOO, guarantees $\tilde{O}(T^{3/4})$ regret w.r.t. the losses and $O(T^{7/8})$ constraints violation (ignoring all quantities except for $T$) . In particular, these bounds hold w.r.t. any interval of the sequence. We also present a more efficient algorithm that requires only first-order oracle access to the soft constraints and achieves similar bounds w.r.t. the entire sequence. We extend the latter to the setting of bandit feedback and obtain similar bounds (as a function of $T$) in expectation.

From Oja's Algorithm to the Multiplicative Weights Update Method with Applications

Oja's algorithm is a well known online algorithm studied mainly in the context of stochastic principal component analysis. We make a simple observation, yet to the best of our knowledge a novel one, that when applied to a any (not necessarily stochastic) sequence of symmetric matrices which share common eigenvectors, the regret of Oja's algorithm could be directly bounded in terms of the regret of the well known multiplicative weights update method for the problem of prediction with expert advice. Several applications to optimization with quadratic forms over the unit sphere in $\reals^n$ are discussed.

Efficiency of First-Order Methods for Low-Rank Tensor Recovery with the Tensor Nuclear Norm Under Strict Complementarity

We consider convex relaxations for recovering low-rank tensors based on constrained minimization over a ball induced by the tensor nuclear norm, recently introduced in \cite{tensor_tSVD}. We build on a recent line of results that considered convex relaxations for the recovery of low-rank matrices and established that under a strict complementarity condition (SC), both the convergence rate and per-iteration runtime of standard gradient methods may improve dramatically. We develop the appropriate strict complementarity condition for the tensor nuclear norm ball and obtain the following main results under this condition: 1. When the objective to minimize is of the form $f(\mX)=g(\mA\mX)+\langle{\mC,\mX}\rangle$ , where $g$ is strongly convex and $\mA$ is a linear map (e.g., least squares), a quadratic growth bound holds, which implies linear convergence rates for standard projected gradient methods, despite the fact that $f$ need not be strongly convex. 2. For a smooth objective function, when initialized in certain proximity of an optimal solution which satisfies SC, standard projected gradient methods only require SVD computations (for projecting onto the tensor nuclear norm ball) of rank that matches the tubal rank of the optimal solution. In particular, when the tubal rank is constant, this implies nearly linear (in the size of the tensor) runtime per iteration, as opposed to super linear without further assumptions. 3. For a nonsmooth objective function which admits a popular smooth saddle-point formulation, we derive similar results to the latter for the well known extragradient method. An additional contribution which may be of independent interest, is the rigorous extension of many basic results regarding tensors of arbitrary order, which were previously obtained only for third-order tensors.

Projection-free Online Exp-concave Optimization

We consider the setting of online convex optimization (OCO) with \textit{exp-concave} losses. The best regret bound known for this setting is $O(n\log{}T)$, where $n$ is the dimension and $T$ is the number of prediction rounds (treating all other quantities as constants and assuming $T$ is sufficiently large), and is attainable via the well-known Online Newton Step algorithm (ONS). However, ONS requires on each iteration to compute a projection (according to some matrix-induced norm) onto the feasible convex set, which is often computationally prohibitive in high-dimensional settings and when the feasible set admits a non-trivial structure. In this work we consider projection-free online algorithms for exp-concave and smooth losses, where by projection-free we refer to algorithms that rely only on the availability of a linear optimization oracle (LOO) for the feasible set, which in many applications of interest admits much more efficient implementations than a projection oracle. We present an LOO-based ONS-style algorithm, which using overall $O(T)$ calls to a LOO, guarantees in worst case regret bounded by $\widetilde{O}(n^{2/3}T^{2/3})$ (ignoring all quantities except for $n,T$). However, our algorithm is most interesting in an important and plausible low-dimensional data scenario: if the gradients (approximately) span a subspace of dimension at most $\rho$, $\rho << n$, the regret bound improves to $\widetilde{O}(\rho^{2/3}T^{2/3})$, and by applying standard deterministic sketching techniques, both the space and average additional per-iteration runtime requirements are only $O(\rho{}n)$ (instead of $O(n^2)$). This improves upon recently proposed LOO-based algorithms for OCO which, while having the same state-of-the-art dependence on the horizon $T$, suffer from regret/oracle complexity that scales with $\sqrt{n}$ or worse.

Faster Projection-Free Augmented Lagrangian Methods via Weak Proximal Oracle

This paper considers a convex composite optimization problem with affine constraints, which includes problems that take the form of minimizing a smooth convex objective function over the intersection of (simple) convex sets, or regularized with multiple (simple) functions. Motivated by high-dimensional applications in which exact projection/proximal computations are not tractable, we propose a \textit{projection-free} augmented Lagrangian-based method, in which primal updates are carried out using a \textit{weak proximal oracle} (WPO). In an earlier work, WPO was shown to be more powerful than the standard \textit{linear minimization oracle} (LMO) that underlies conditional gradient-based methods (aka Frank-Wolfe methods). Moreover, WPO is computationally tractable for many high-dimensional problems of interest, including those motivated by recovery of low-rank matrices and tensors, and optimization over polytopes which admit efficient LMOs. The main result of this paper shows that under a certain curvature assumption (which is weaker than strong convexity), our WPO-based algorithm achieves an ergodic rate of convergence of $O(1/T)$ for both the objective residual and feasibility gap. This result, to the best of our knowledge, improves upon the $O(1/\sqrt{T})$ rate for existing LMO-based projection-free methods for this class of problems. Empirical experiments on a low-rank and sparse covariance matrix estimation task and the Max Cut semidefinite relaxation demonstrate the superiority of our method over state-of-the-art LMO-based Lagrangian-based methods.

Low-Rank Mirror-Prox for Nonsmooth and Low-Rank Matrix Optimization Problems

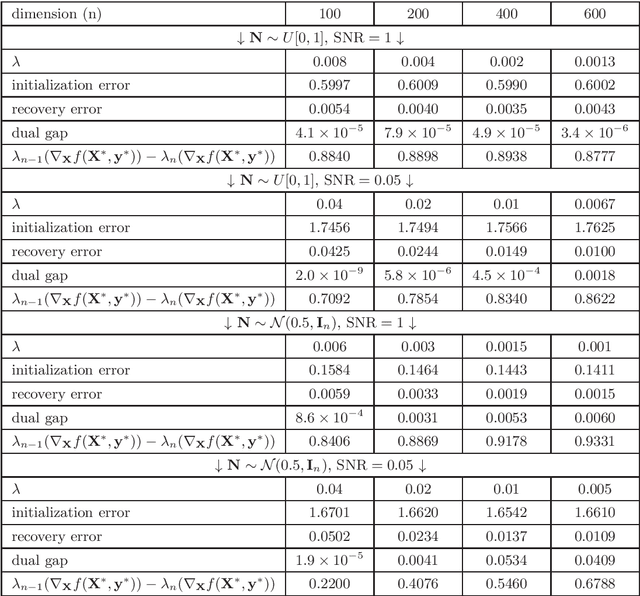
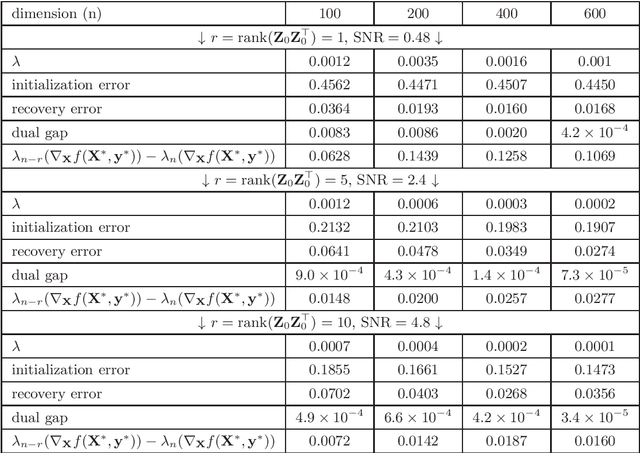
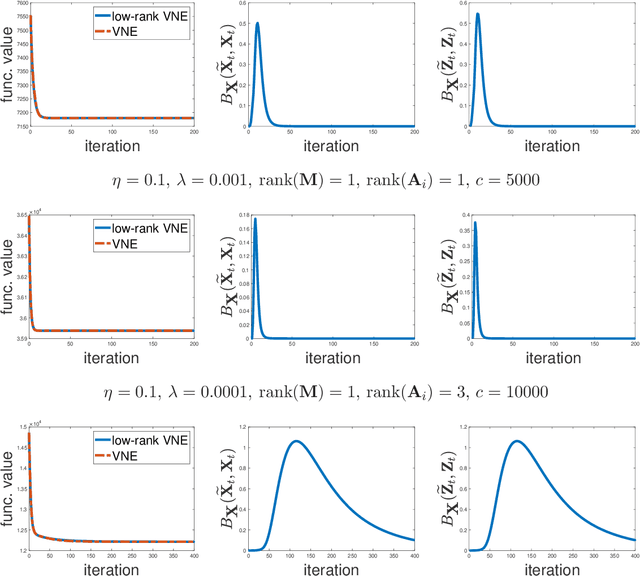
Low-rank and nonsmooth matrix optimization problems capture many fundamental tasks in statistics and machine learning. While significant progress has been made in recent years in developing efficient methods for \textit{smooth} low-rank optimization problems that avoid maintaining high-rank matrices and computing expensive high-rank SVDs, advances for nonsmooth problems have been slow paced. In this paper we consider standard convex relaxations for such problems. Mainly, we prove that under a \textit{strict complementarity} condition and under the relatively mild assumption that the nonsmooth objective can be written as a maximum of smooth functions, approximated variants of two popular \textit{mirror-prox} methods: the Euclidean \textit{extragradient method} and mirror-prox with \textit{matrix exponentiated gradient updates}, when initialized with a "warm-start", converge to an optimal solution with rate $O(1/t)$, while requiring only two \textit{low-rank} SVDs per iteration. Moreover, for the extragradient method we also consider relaxed versions of strict complementarity which yield a trade-off between the rank of the SVDs required and the radius of the ball in which we need to initialize the method. We support our theoretical results with empirical experiments on several nonsmooth low-rank matrix recovery tasks, demonstrating both the plausibility of the strict complementarity assumption, and the efficient convergence of our proposed low-rank mirror-prox variants.

Frank-Wolfe-based Algorithms for Approximating Tyler's M-estimator

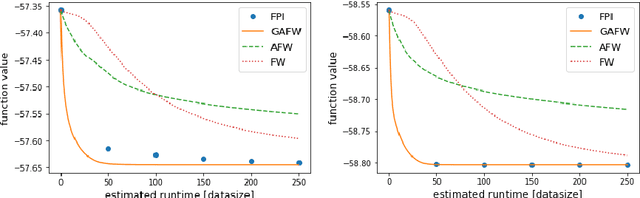
Tyler's M-estimator is a well known procedure for robust and heavy-tailed covariance estimation. Tyler himself suggested an iterative fixed-point algorithm for computing his estimator however, it requires super-linear (in the size of the data) runtime per iteration, which may be prohibitive in large scale. In this work we propose, to the best of our knowledge, the first Frank-Wolfe-based algorithms for computing Tyler's estimator. One variant uses standard Frank-Wolfe steps, the second also considers \textit{away-steps} (AFW), and the third is a \textit{geodesic} version of AFW (GAFW). AFW provably requires, up to a log factor, only linear time per iteration, while GAFW runs in linear time (up to a log factor) in a large $n$ (number of data-points) regime. All three variants are shown to provably converge to the optimal solution with sublinear rate, under standard assumptions, despite the fact that the underlying optimization problem is not convex nor smooth. Under an additional fairly mild assumption, that holds with probability 1 when the (normalized) data-points are i.i.d. samples from a continuous distribution supported on the entire unit sphere, AFW and GAFW are proved to converge with linear rates. Importantly, all three variants are parameter-free and use adaptive step-sizes.

New Projection-free Algorithms for Online Convex Optimization with Adaptive Regret Guarantees

We present new efficient \textit{projection-free} algorithms for online convex optimization (OCO), where by projection-free we refer to algorithms that avoid computing orthogonal projections onto the feasible set, and instead relay on different and potentially much more efficient oracles. While most state-of-the-art projection-free algorithms are based on the \textit{follow-the-leader} framework, our algorithms are fundamentally different and are based on the \textit{online gradient descent} algorithm with a novel and efficient approach to computing so-called \textit{infeasible projections}. As a consequence, we obtain the first projection-free algorithms which naturally yield \textit{adaptive regret} guarantees, i.e., regret bounds that hold w.r.t. any sub-interval of the sequence. Concretely, when assuming the availability of a linear optimization oracle (LOO) for the feasible set, on a sequence of length $T$, our algorithms guarantee $O(T^{3/4})$ adaptive regret and $O(T^{3/4})$ adaptive expected regret, for the full-information and bandit settings, respectively, using only $O(T)$ calls to the LOO. These bounds match the current state-of-the-art regret bounds for LOO-based projection-free OCO, which are \textit{not adaptive}. We also consider a new natural setting in which the feasible set is accessible through a separation oracle. We present algorithms which, using overall $O(T)$ calls to the separation oracle, guarantee $O(\sqrt{T})$ adaptive regret and $O(T^{3/4})$ adaptive expected regret for the full-information and bandit settings, respectively.